In mathematics, we study probability. Probability is so familiar in our lives and all statistics are based on probability.
If you learn probability, you will be able to understand what is going on in the news. Also, experimental data in science is processed using probability. Whether or not it will rain in a weather forecast is also a probability. If you do not understand probability, you will not be able to read and understand data correctly, which will cause problems when you spend your daily life as an adult.
That’s why we study probability in mathematics. Mathematics must be learned in order to use it in everyday life, and probability is a type of mathematics. When learning the basics of probability in mathematics, one of the most frequently used examples is the probability of coins and dice.
What are the probabilities when we toss two or more coins or dice? We will explain the basics of probability as taught in mathematics.
Table of Contents
What Is Probability? The Percentage of Probability that Occurs
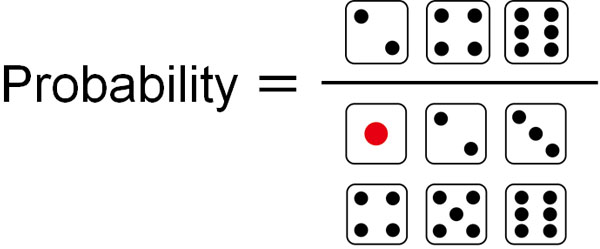
First of all, what is probability? Probability is the rate at which a particular event occurs. For example, when you roll the dice, what is the probability of getting a 4? For this, anyone can answer that the probability is $\displaystyle\frac{1}{6}$.
If you roll the dice, you can expect to get a 4 at some point if you roll the dice 6 times. Of course, you might get a 4 on the first roll of the dice. In some cases, you may finally get a 4 on the 20th roll. In any case, the probability of getting a 4 on the dice is $\displaystyle\frac{1}{6}$.
So how do we get the probability? In the case of dice, there are numbers from 1 to 6. In other words, there are six different ways to get the number. Out of the six possible ways, only one will result in the number 4. Therefore, the probability is $\displaystyle\frac{1}{6}$.
Hence, in probability, the following formula holds.

In calculating probability, be sure to count the number of times of the total event. For dice, there are six different results. Out of them, we can put the number of times a particular event will occur in the numerator to get the probability.
For example, what is the probability of getting an even number on the dice? Even and odd numbers are frequently asked in probability, so we need to understand how to solve them.
As mentioned above, dice have 1-6 different outcomes. Of these, 2, 4, and 6 are even numbers. In other words, there are three possible ways to get an even number. So the probability of getting an even number on the dice is $\displaystyle\frac{3}{6}$. However, the answer is $\displaystyle\frac{1}{2}$, since we need to reduce a fraction.
We can use the same method to come up with probabilities for odd numbers. When calculating probabilities in mathematics, try to think about how many ways there are in total and how many times the particular event will occur.
Equally Possible Means Same Frequency of Occurrence
However, when calculating probability, there is a precondition. That precondition is called “equally possible”. What does equally possible mean?
When we roll the dice, the probability of getting 4 is $\displaystyle\frac{1}{6}$, as mentioned above. So, for the following dice, is the probability of getting a 4 $\displaystyle\frac{1}{6}$?
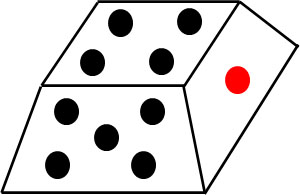
We can predict that the probability of getting a 4 is much higher than $\displaystyle\frac{1}{6}$. Why is the probability of getting a 4 not $\displaystyle\frac{1}{6}$ despite the dice? The reason is that the shape of the dice is biased to make it easier to get a particular number.
The calculation of probability requires the assumption that the probability of occurrence is the same for all events. This is equally possible.
For example, when betting, in many cases, the challenger loses. One reason for this is that cheating takes place. In betting, there are few cases that are equally possible. If it is not equally possible, we cannot calculate the probability.
Calculating the Probability of the Front and Back of Two Coins
Let’s actually calculate the probability. In calculating probability, we will consider a situation in which two coins are tossed. When we learn the basics of probability in mathematics, we often use coins as an example to learn probability.
A coin has two sides; heads and tails. The probability of tossing a coin and getting heads or tails is $\displaystyle\frac{1}{2}$. So what is the probability if we toss two coins?
When calculating the probability, if you think intuitively, you will get an incorrect answer with a high possibility. Therefore, you have to understand the correct way to get the probability. For example, what is the probability that the two coins will both be heads? Those who get it wrong will answer $\displaystyle\frac{1}{3}$. This is because we think there are the following patterns.
- Front, Front
- Front, Back
- Back, Back
So, let’s think more precisely. For example, suppose we have the following two coins (5 and 10).
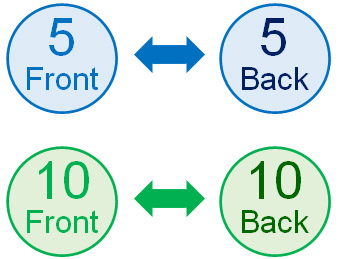
If you toss two coins, you can understand that there are four patterns.
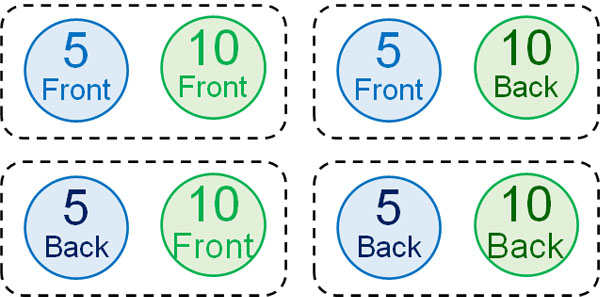
There is more than one front-back pair. There are two types: (front, back) and (back, front). Therefore, the total number of events to occur is four. Therefore, the probability of tossing two coins and having them both be heads is $\displaystyle\frac{1}{4}$.
Find the Probability by Tree Diagram
However, it is difficult to write down all the events without a hint. How can we find all the events efficiently? One way is using tree diagrams. A tree diagram allows you to write down all the events.
In a tree diagram, we first focus on a single event. When we focus on a single coin, we get either front or back. Therefore, we can draw a tree diagram as follows.
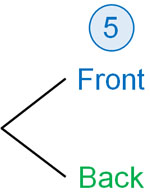
Then toss the other coin. As a result, we can see that there are four ways as follows.

In other words, a tree diagram is a way to write out all the different types of events. Whether you toss a coin at the same time or separately, the result is the same. So, by using a tree diagram, you can check all the possible events.
Not Drawing a Tree Diagram Is Likely to Be Incorrect
As mentioned above, many people make miscalculations when they calculate probability intuitively. In other words, if you do not draw a tree diagram, you will make many calculation mistakes.
The reason why miscalculations occur when tossing two coins is that many people think of situations in which they toss the same type of coin. What is the probability that both coins will be on the front side when tossing the same two coins, as shown below?

Even if they are the same coin, the way of thinking is the same as before. Whether the coins are the same or different, the probability is the same. Just because the coin is the same does not mean that the probability will change.
In this case, since the coins are the same, we need to think of the tree diagram with different criteria. So, let’s separate the first coin and the second coin. Although we are actually tossing two coins at the same time, we assume that they are tossed separately for the purpose of drawing the tree diagram. Then we have the following.
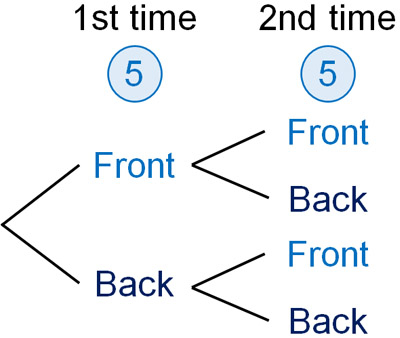
When drawing a tree diagram, assume that events occur separately rather than simultaneously. That way, you can draw all the outcomes.
Then, check the number of times the event is happening from the tree diagram. For example, when tossing two coins, it would be as follows.
- Both front: one
- One side front, the other side back: two
- Both back: one

By drawing a tree diagram, we can find out the number of times of the total event. Not only that, we can count how many times a particular event has occurred. When learning the basics of probability in mathematics, be sure to draw a tree diagram.
The Probability of Rolling Two Dice
After understanding the probability of coins, let’s learn about the probability of rolling two dice. In the basics of probability, the dice are a frequently asked question.
Whether the two dice are the same or different sizes, the result is the same. We have explained that the idea of probability is the same regardless of whether the coins are the same or different. If we draw a tree diagram, the answer will be the same for both. The same is true for dice, not coins.
So, how should we think of a tree diagram for two dice? First, when you roll the dice the first time, there are six possible outcomes. Then, when you roll the dice a second time, there are six possible outcomes for each.
In fact, we roll the dice at the same time. However, as explained so far, we make a tree diagram assuming that the dice are rolled separately. In that case, we get the following.
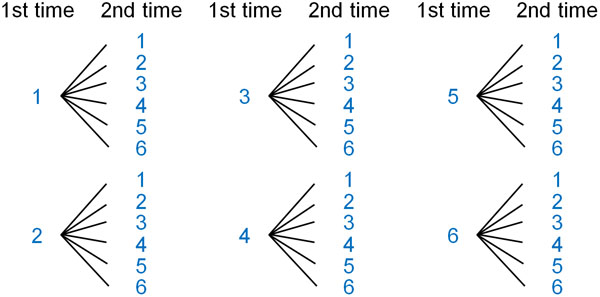
The first dice has 6 ways, and the second dice has 6 ways. Therefore, there are $6×6=36$ events.
However, in the case of dice, the tree diagram is more complicated and difficult to distinguish. Also, it takes time to create a tree diagram. So, when rolling two dice at the same time, it is common in mathematics to create the following table.
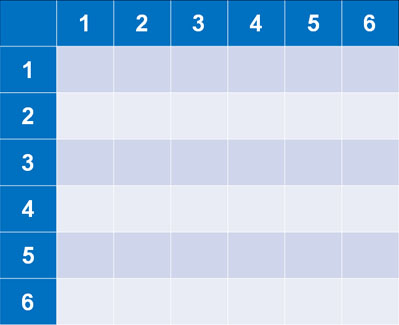
It is not available if we roll three dice. However, this table is useful in the case of rolling two dice.
For example, if you roll two dice, what is the probability that the multiplication will result in 12? If we want to find this probability, check the box where multiplication will result in 12. It will look like the following.
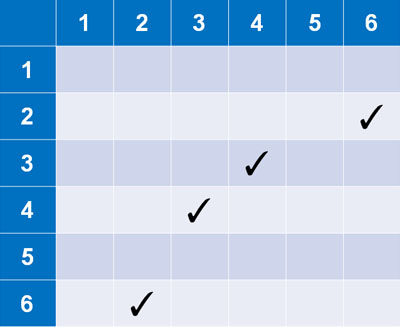
In the table, there are four ways in which the result will be 12. Since the total number of events is 36, the probability of rolling two dice and getting a result of 12 is $\displaystyle\frac{4}{36}$. Also, by reducing the fraction, the answer becomes $\displaystyle\frac{1}{9}$.
Calculate the Probability of Not Occurring
In mathematics probability, sometimes we have to calculate the probability of not happening. The probability of an event occurring can be calculated using the method described so far. On the other hand, how can we calculate the probability of non-occurrence?
When calculating the probability of non-occurrence, the idea is the same as in the previous explanations. First, try to find the probability of occurrence.
For example, suppose there is a lottery that has a 20% chance of winning. In this case, what is the probability that you will not win the lottery? The calculation method is as follows.
- 100% – 20% = 80%
There are only two types of lotteries: winning and losing. Therefore, by subtracting the probability of winning from 100%, we get the probability of not winning (the probability of not happening).
Of course, the idea is the same for fractions instead of percentages. 20% has the same meaning as $\displaystyle\frac{1}{5}$. In other words, the probability of winning is $\displaystyle\frac{1}{5}$. In this case, the probability of not winning is as follows.
- $1-\displaystyle\frac{1}{5}=\displaystyle\frac{4}{5}$
100% = 1. Once we understand these facts, we can determine the probability of not happening by the following formula.
- Probability of not happening $=1-$ Probability of happening
In this way, we can find the probability that it will not happen. Understand not only the probability of happening but also how to get the probability of not happening.
Exercises: Probability Calculation Problems
Q1: Solve the following problem.
Two dice are rolled. After squaring the numbers on the dice and adding the two numbers, find the probability that the number of dice is less than or equal to 30.
A1: Answer.
In dice problems, be sure to make a table. After making the table, square each number. Then add them up and check the part that is less than or equal to 30. It will look like this.
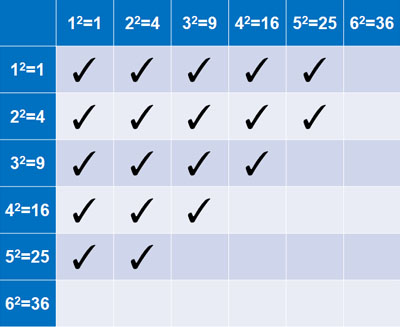
The total number of events is 36. Also, the number of checks is 19. Therefore, we have the following probability.
- $\displaystyle\frac{19}{36}$
Q2: Solve the following problem
There are three envelopes with numbers 1 to 3 written on them. Also, there are three cards with the numbers 1 to 3 written on them.
Then, put all the cards into each envelope. What is the probability that the numbers on the envelopes and the cards are all different?
A2: Answer.
Without drawing a tree diagram, we can’t solve the problem. So, let’s draw a tree diagram.
What if we put card 1 in envelope 1? In this case, we can put either card 2 or 3 in envelope 2. Then, we would put the remaining card in envelope 3.
In the same way, we will draw a tree diagram, considering the case of putting card 2 in envelope 1 and the case of putting card 3 in envelope 1. Then we will have the following.
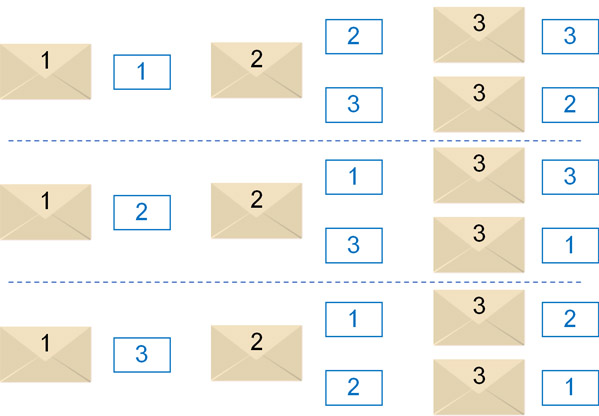
Thus, we can see that there are six ways in total. In which of these cases are the numbers on the envelope and the card all different? If you count them one by one, there are two such events.
- Envelope 1 (card 2), envelope 2 (card 3), envelope 3 (card 1)
- Envelope 1 (card 3), envelope 2 (card 1), envelope 3 (card 2)
Therefore, the probability is as follows.
- $\displaystyle\frac{2}{6}=\displaystyle\frac{1}{3}$
Learn the Basics of Probability and Do the Calculations
When learning the basics of probability in mathematics, you don’t learn difficult formulas from the beginning. By using a tree diagram, we can figure out what patterns are there, one by one. Therefore, you cannot get an answer without drawing a diagram.
If you solve a problem without a tree diagram, you are almost certain to get an incorrect answer. This is because, as explained in the coin example, without a diagram, mistakes will occur frequently.
Probability problems are more challenging because all patterns need to be shown. Not only that, you have to count how many of the target events have occurred.
By doing these things one by one, you will know what the probability of occurrence is. At the same time, you will be able to calculate the probability that it will not happen. When learning probability, understand these basic concepts.