In mathematics, we learn about plane shapes. One of the important topics is the vertical angle, corresponding angle, and alternate angle. These three angles are frequently encountered in problems involving figures. Therefore, it is a concept that you must understand.
So, what are vertical angles, corresponding angles, and alternate angles? And what are their properties?
The key to these three angles is the idea that the angles are the same. If you think about why the angles are equal, you will be able to understand mathematics more deeply. The proof is simple, so let’s also understand why angles are equal.
In this section, we will explain the properties of vertical angles, corresponding angles, and alternate angles, which are important in plane figures, including the reasons.
Table of Contents
The Vertical Angle in Plane Figures Has the Same Angle
In the types of angles in plane figures, we learn about the vertical angle. What are vertical angles? The vertical angles are the angles that face each other when two lines intersect.
For example, the following are vertical angles.
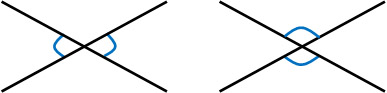
The angles that have this relationship are called vertical angles. The important thing to remember is that vertical angles are always equal. Remember that if there are two vertical angles, ∠A and ∠B, then ∠A = ∠B.
Proof That the Angles Are the Same
So, why are the vertical angles equal? This proof can be explained by the mathematical knowledge we have learned so far.
For example, suppose we have ∠A and ∠B with the following relationship.
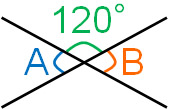
The angle of a straight line is 180°. Therefore, the angle of ∠A can be calculated as follows.
- $180°-120°=60°$
In the same way, ∠B can be calculated as follows.
- $180°-120°=60°$
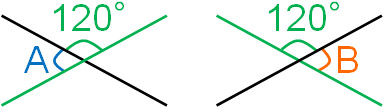
In this calculation, we have assumed 120°. Even if we assume that the angles are different, ∠A and ∠B will always be the same angle. Thus, we can prove that the vertical angles are always the same.
Understanding Relationship Between Corresponding Angles and Alternate Angles
Once you understand the vertical angles, next you need to learn about corresponding angles. Corresponding angles are the angles formed by the intersection of two lines. The angles that have the following relationship are corresponding angles.
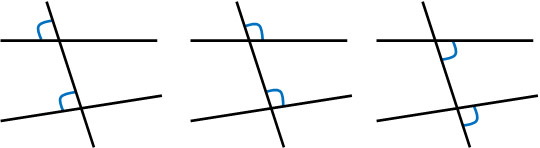
Try to understand corresponding angles with an image; angles that are in the same position for two lines are corresponding angles.
In plane figures, we will also learn about alternate angles. Angles with the following relationship are alternate angles.

Whenever there are corresponding angles, there are also alternate angles. It is very difficult to explain the corresponding angles and the alternate angles in a sentence. So, let’s use the image above to remember what kind of angles they are.
In Parallel Lines, Corresponding and Alternate Angles Have Same Angles
The important case of corresponding and alternate angles is when the two lines are parallel. When two lines are parallel, we have the following.
- Corresponding angles are equal.
- Alternate angles are equal.

If the two lines are not parallel, the corresponding angles are not equal. Likewise, the alternate angles are not equal. Even if the lines are not parallel, the corresponding angles and the alternate angles still exist. However, in order for the corresponding angles and the alternate angles to be the same respectively, the two lines need to be parallel.
-Corresponding Angle and Alternate Angle Are Equal
If we understand these, we can see that when two lines are parallel, the corresponding angle and the alternate angle are equal. This is because the corresponding angle and alternate angle are vertical angle relationships.

So understand that for parallel lines, both the corresponding angle and the alternate angle are the same angle.
-The Symbol for Parallel Is ||
The symbol for parallelism is ||. For example, in the case of $l||m$, it means that the lines $l$ and $m$ are parallel.
The Reason Why Angles Are the Same
So, when two lines are parallel, why do the corresponding angles and the alternate angles have the same angles? Let’s think about this reason. When thinking about this reason, use a triangular ruler.
If we slide a triangular ruler and draw a line, we can draw two parallel lines. It is the following.
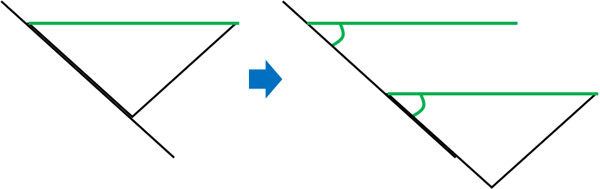
As a result, we can create corresponding angles for two parallel lines. Since we are using the same triangle ruler, the corresponding angles are the same. Thus, we can see that the corresponding angles are the same for parallel lines. We can understand why the corresponding angles are the same by drawing the figures without having to prove them with numbers.
Also, as mentioned above, the alternate angles and the corresponding angles are vertical angle relationships. Therefore, if two lines are parallel, we can understand that the alternate angles are equal.
There Are Four Patterns of Alternate Angles
It is easy for anyone to understand the corresponding angles. On the other hand, when learning about alternate angles for the first time, it is difficult to distinguish them. So, let’s try to remember the different patterns of alternate angles. Specifically, we should divide the alternate angles into four patterns.
When understanding alternate angles, we can divide them into the following four types.
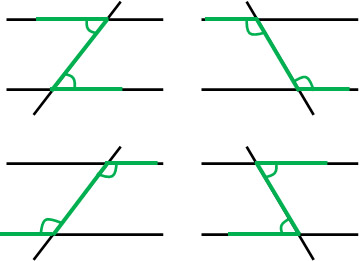
In alternate angles, they all have a Z shape. In some cases, it may be an opened Z, or it may be a crushed Z. But in any case, the shape of the Z is the alternate angle.
Exercises: Vertical, Corresponding, and Alternate Angles
Q:. If $l||m$, answer the angles from a to d.
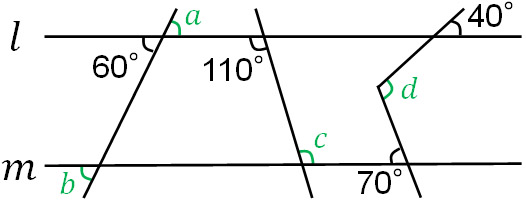
A1: Answers.
(a, b, c)
Answer the vertical, corresponding, and alternate angles, respectively.
- a: 60° (Vertical angle)
- b: 60° (Corresponding angle)
- c: 110° (Alternate angle)
(d)
In the advanced questions, you will be asked to find the angle of d. Without doing anything, it is not possible to answer the angle of d. So, let’s add the parallel lines as follows.
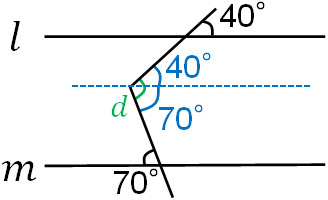
By adding the lines in this way, we can find the angle of d. By using the corresponding angle and the alternate angle, we know that one angle is 40° and the other is 70°. So by adding the two angles, we get d = 110°.
When answering the angle in a plane figure, it is often that you need to add parallel lines to solve the problem. When you are given a problem statement, instead of not adding any lines, actively try to add lines. There are many problems that can be answered simply by drawing parallel lines.
Learn the Rule of Equality of Angles in Plane Figures
Angle problems are frequently asked in mathematics. When learning about angles, vertical angles, corresponding angles, and alternate angles are the basics. If you do not understand these concepts, you will not be able to solve subsequent math problems.
Reviewing the properties of angles, we can see the following.
- Vertical angle: The angles are always equal.
- Corresponding angle: If lines are parallel, the angles are equal.
- Alternate angle: If lines are parallel, the angles are equal.
In addition to calculating angles, we also use vertical angles, corresponding angles, and alternate angles in many situations in mathematics, such as proofs of congruence or similarity. So, make sure you understand the meaning and characteristics of these angles.





