In mathematics, we learn about quadratic functions. A graph that has a square and is a quadratic function, and a graph has a curve.
In mathematics involving graphs, we first learn direct proportions. The graphs that apply direct proportions are linear functions. Further advancement of linear functions is quadratic functions. The concept of linear and quadratic functions is almost the same; the only difference is whether or not $x^2$ is included in the equation.
However, the shape of the graph is quite different in quadratic functions. There are also some characteristics of quadratic functions that you need to remember.
In addition, quadratic functions are often used with linear functions in problems. In this section, we will explain how to solve quadratic function problems.
Table of Contents
Equations with $y=ax^2$ Are Quadratic Functions
When we substitute a number for $x$, the equation that clearly determines the value of $y$ is a function. In a linear function, for example, we have the following equation.
- $y=x+2$
In such an equation, if $x$ is doubled, the increase in $y$ is also doubled. Therefore, the values of $y$ and $x$ are in a proportional relationship.
On the other hand, in quadratic functions, for example, the equation is as follows.
- $y=x^2$
In this case, if the value of $x$ is doubled, the value of $y$ is 22 times (four times). In other words, the value of $y$ is proportional to $x^2$. As the value of $x$ increases, the value of $y$ increases by the square.
In quadratic equations, for example the following.
- $y=5x^2$
- $y=-3x^2$
- $y=x^2$
- $y=\displaystyle\frac{1}{2}x^2$
Thus, the number in front of $x^2$ changes depending on the expression. Therefore, the quadratic function is represented by the following formula,
- $y=ax^2$
The most basic quadratic function is expressed by $y=ax^2$.
Many Natural Phenomena Involve Quadratic Functions
Why do we need to learn quadratic functions? It’s because many of the phenomena around us involve quadratic functions.
For example, when you place a ball on a slope and release it, what happens to the speed of the ball? Right after you take your hand off the ball, the speed of the ball is slow. However, over time, the speed of the ball will gradually increase. It is not proportional, which is always a constant speed, but a quadratic function, which increases in speed as time goes by.
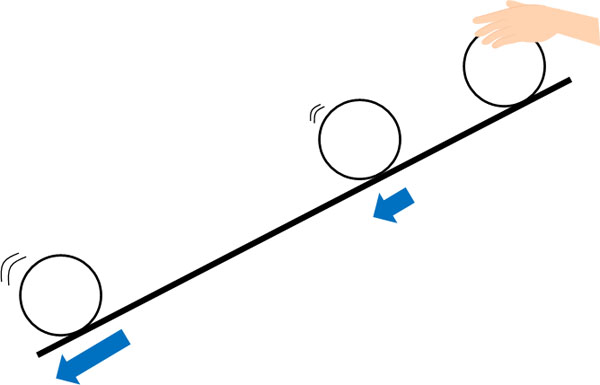
In other cases, when a stationary car speeds up, the speed increases in a quadratic function. Of course, we use quadratic functions not only for cars, but also for calculating the speed of a rocket launch. It is important to understand that quadratic functions are used in various situations.
Table of Quadratic Functions Is Proportional to $x^2$
What does a quadratic function look like in a table? Unlike direct proportions, as mentioned above, quadratic functions are proportional to $x^2$.
For example, in equation $y=x^2$, the table looks like this.

If $x$ is doubled, $y$ is quadrupled. If $x$ is tripled, $y$ is multiplied by 9. If $x$ is quadrupled, $y$ is multiplied by 16.
Since the equation is $y=x^2$, as the value of $x$ increases, the value of $y$ is $x$ squared. It is important to note that the value of $y$ is an expression that increases by the square.
Quadratic Functions Become a Parabolic Graph
What does a quadratic formula look like when you graph it? For example, the graph of $y=x^2$ looks like this.

As you can see, it is a curved graph. To draw a graph, plot the coordinates of $x$ and $y$ on the graph. Then we can graph a quadratic function by connecting the coordinates with a smooth curve.
The graph of $y=ax^2$ will always pass through the origin. Also, the quadratic function of $y=ax^2$ passes through the coordinates of $(0,0)$.
Note that the curve on the graph of the quadratic function is the same as the trajectory of the ball when it is thrown. In fact, when you throw an object in the air, you can calculate its speed using the quadratic function.

Earlier, we explained that the trajectory of a rocket is calculated by a quadratic function. The reason for this is that rockets fly in the air. Also, in the past, quadratic functions were used to calculate the trajectory of cannon fire. Quadratic functions are used in various situations, including science technology, and warfare.
The line on the graph of a quadratic equation is called a parabola. Any object in the air will follow a parabola and will have the same curve as the quadratic function.
The Value of $a$ Changes the Shape of the Graph
When we draw a graph of $y=ax^2$, consider that the shape of the graph depends on the value of $a$. The larger the absolute value of $a$, the steeper the graph becomes. On the other hand, the smaller the absolute value of $a$, the looser the graph becomes.
The shape of the graph depends on the value of $a$, as shown below.
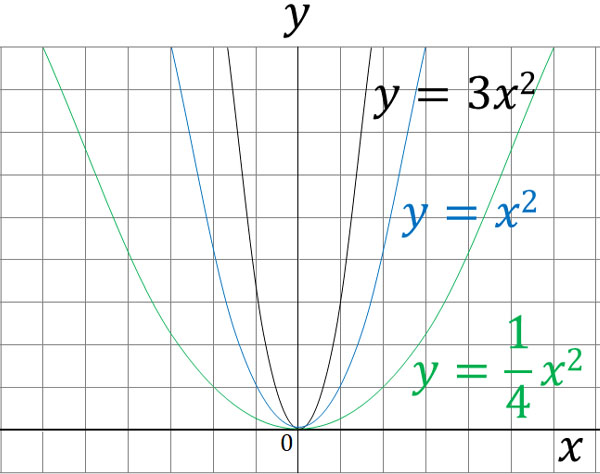
All graphs pass through the origin $(0,0)$. It is also the same that the curve is a parabola. The difference is that the shape of the graph changes depending on the value of $a$.
Convex Downward for $a>0$ and Convex Upward for $a<0$
There is also another important point. The direction of the graph changes depending on whether the value of $a$ is a positive number or a negative number.
In the graph of a quadratic function, if $a$ is a positive number ($a>0$), it will be convex downward. On the other hand, if $a$ is a negative number ($a<0$), it will be convex upward. Specifically, it looks like the following.
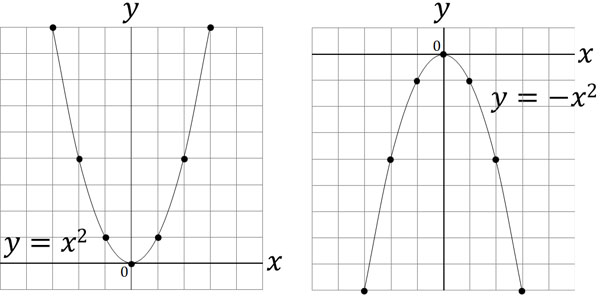
In a quadratic function, the value of $x$ is squared. So whether the value of $x$ is positive or negative, the answer will always be positive.
But in a quadratic function, you multiply the value of $a$. Therefore, if the value of $a$ is positive, the larger the value of $x$ is, the larger the value of $y$ will be. On the other hand, if the value of $a$ is negative, the larger the value of $x$ is, the smaller the value of $y$ will be.
The Rate of Change in Quadratic Functions Varies
In a quadratic function, we may need to find the rate of change. When calculating a linear function, the rate of change is very important. This is because the rate of change is the slope. By calculating the rate of change, we can get the slope $a$.
However, the way of thinking about the rate of change is different between linear and quadratic functions. For a linear function, the rate of change is always the same. In quadratic functions, on the other hand, the rate of change varies from place to place.
The following formula is used to calculate the rate of change.
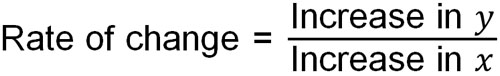
We don’t need to remember this formula for linear functions. As mentioned earlier, the rate of change and the slope have the same meaning. On the other hand, what about quadratic functions? Even for quadratic functions, there is no point in remembering the rate of change formula.
The rate of change is, in essence, how much the value of $y$ increases when the value of $x$ increases by 1. If you understand this definition, you don’t need to remember the rate of change formula. We can use the properties of the ratio. It looks like the following.
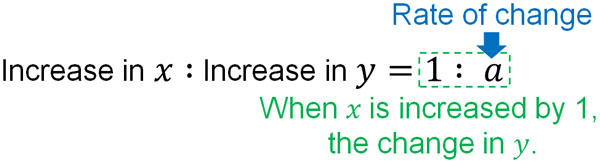
By using the properties of ratios, you can come up with a rate of change. For example, we have the following.
- When the value of $x$ is increased by 1, the value of $y$ is increased by 2: the rate of change is 2
- When the value of $x$ is increased by 1, the value of $y$ is increased by -4: the rate of change is -4
- When the value of $x$ is increased by 7, the value of $y$ is increased by 3: the rate of change is $\displaystyle\frac{3}{7}$
For example, if the value of $x$ is increased by 7 and the value of $y$ is increased by 3, the ratio is $7:3=1:a$. Solving for this, we have $a=\displaystyle\frac{3}{7}$. If you remember a formula that is used infrequently and is not important, you are sure to forget it. Rather, you have to understand the principles of why it happens and come up with a value without a formula.
In mathematics, there are situations where we have to remember formulas and situations where we don’t. For the rate of change, there is no point in remembering the formula.
-The Rate of Change in Quadratic Equations
As mentioned above, the rate of change in a quadratic function varies depending on the coordinates. How do we calculate the rate of change in a quadratic function? As an example, let’s calculate the rate of change for the graph of $y=x^2$ in the following case.
- When the value of $x$ changes from 1 to 2
- When the value of $x$ changes from -3 to -1
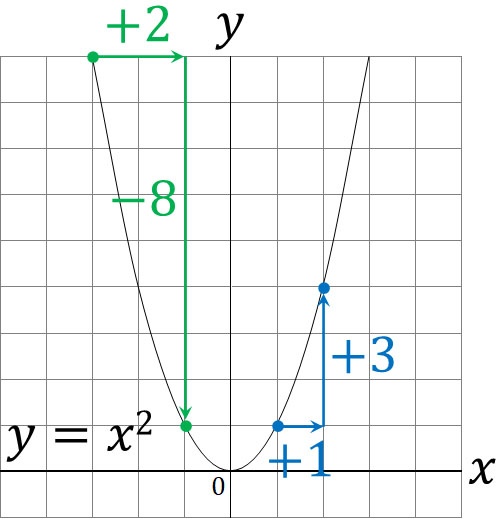
When the value of $x$ changes from 1 to 2, the value of $y$ increases by 3. When $x$ increases by 1, $y$ increases by 3, so the rate of change is 3.
On the other hand, when the value of $x$ changes from -3 to -1, the value of $y$ increases by -8. When $x$ increases by 2, $y$ increases by -8. The ratio of change is -4 because $2:-8=1:a$.
Find a Linear Function Through Two Points
Why do we need to find the rate of change in quadratic functions? It is because we have to solve a problem that combines a quadratic function and a linear function, as shown below.
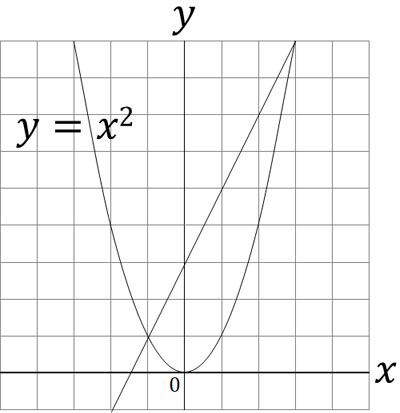
While the rate of change in quadratic functions changes, the rate of change in linear functions does not change. Therefore, for a quadratic function, the rate of change is always constant for the line connecting the two coordinates. This is because the slope is the rate of change.
Finding the rate of change in a quadratic function is the same meaning as finding the slope of a line connecting two coordinates. For reference, in the previous graph, $(-1,1)$ and $(3,9)$ are the intersection points. In other words, an increase of $x$ by 4 results in an increase of $y$ by 8.
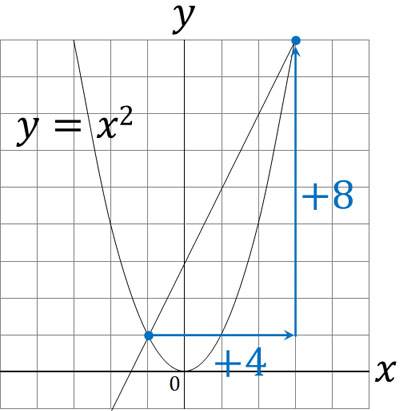
Substituting “Increase in $x$: increase in $y$ = 1 : $a$,” we get $4:8=1:a$. Solving for this, we get $a=2$.
Also, if we check the line passing through the coordinates of the two points, we can see that it passes through the coordinates of $(0,3)$. In other words, the intercept is 3. Therefore, the linear function passing through the intersection of the two points is the following.
- $y=2x+3$
Thus, in a quadratic function, we can find the linear function of the line connecting the two coordinates. This kind of mathematical calculation problem is frequently given as an advanced problem in quadratic functions, so it is important to be able to solve it.
Exercises: Quadratic Function Graph Problems
Q1: Solve the following problems.
We have the graph of $y=ax^2$ (1) and the graph of $y=ax+b$ (2). The origin is O, and the intersection of (1) and (2) is A and B. The $x$-coordinate of A is -2, and the $x$-coordinate of B is 6. Also, set C as the intersection of the line in (2) and the $x$-coordinate.
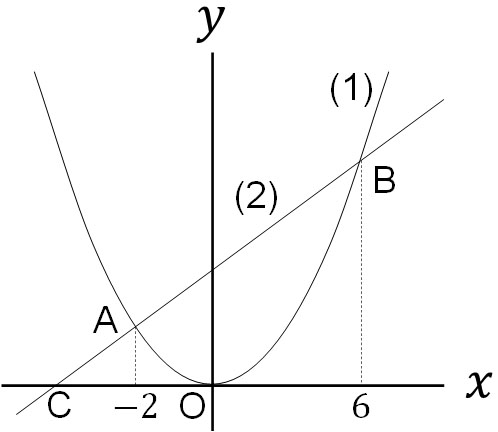
- For the graph in (1), when the value of $x$ increased from -6 to -2, the value of $y$ increased by -16. Let’s find the value of $a$.
- Find the equation for the line in (2).
- Find the area of △AOB.
- Take the point D on the graph in (1). If the area of △COD is 27, find the $x$-coordinates of point D.
A1: Answers.
In quadratic function problems, it is not always the case that only problems related to quadratic functions are given. It is usually a complex of many problems, such as linear functions, simultaneous equations, graphs, etc., related to quadratic functions, as in this problem.
(a)
How can we get an expression for a quadratic function from the rate of change? To do this, consider the amount of increase in $x$ and $y$.
When the value of $x$ is increased from -6 to -2, the value of $x$ is increased by 4. How much does the value of $y$ increase in this case? Substitute into the formula $y=ax^2$.
If the value of $x$ is -6, $y=a×(-6)^2=36a$. If the value of $x$ is -2, $y=a×(-2)^2=4a$. $y$ has increased by -32a because it has changed from 36a to 4a.
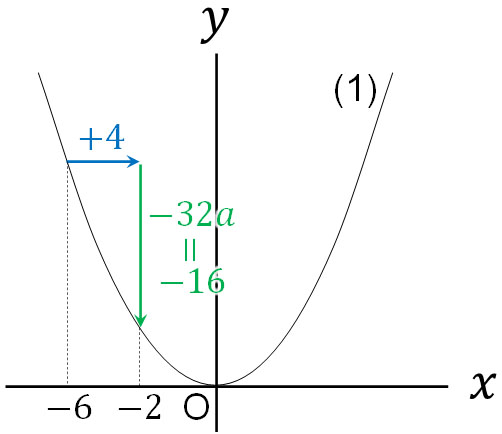
Since we already know that the change in $y$ is -16, we can calculate the following.
$-32a=-16$
$a=\displaystyle\frac{-16}{-32}$
$a=\displaystyle\frac{1}{2}$
Thus, the function in (1) is found to be $y=\displaystyle\frac{1}{2}x^2$.
(b)
Since $y=\displaystyle\frac{1}{2}x^2$, we know the coordinates of A and B. By substituting the value of $x$, we can see that we get the following coordinates, respectively.
- A$(-2,2)$
- B$(6,18)$
If we know the two coordinates, we can solve the linear equation using simultaneous equations. In other words, we can find equation (2). By substituting $y=ax+b$, we solve the following simultaneous equation.
$\begin{eqnarray} \left\{\begin{array}{l}2=–2a+b\\18=6a+b\end{array}\right.\end{eqnarray}$
By solving this system of linear equations, we can get the equation for a linear function.
By the way, it is also possible to get the equation (2) by another method. The other way is to use the rate of change. Since we learned about the rate of change in quadratic functions, let’s use the rate of change to get the equation (2).
Comparing point A and point B, what is the rate of change: when moving from A $(-2,2)$ to B $(6,18)$, the value of $x$ increases by 8, and the value of $y$ increases by 16. The rate of change represents how much the value of $y$ increases when the value of $x$ increases by 1. Therefore, we have the following ratio.
- $8:16=1:a$
Using the properties of the ratio, we can calculate the following.
$16=8a$
$a=2$
Thus, we find that the slope (ratio of change) of the linear function in (2) is 2. Therefore, the formula for the linear function is $y=2x+b$.
Then let’s get the intercept by substituting A $(-2,2)$ or B $(6,18)$. For example, substituting $(6,18)$ yields the following
$18=2×6+b$
$18=12+b$
$b=6$
Thus, we find that the linear function in (2) is $y=2x+6$.
(c)
How do we calculate the area of △AOB? Let P be the intercept (intersection with the $y$-coordinate) in (2), and we will find the following.
- $△AOB=△AOP+△BOP$
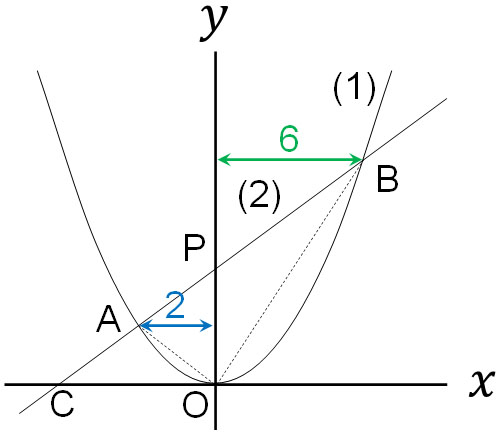
So, let’s find the areas of △AOP and △BOP. Since equation (2) is $y=2x+6$, the coordinate of P is $(0,6)$. In other words, the vertical length of the triangle (line segment PO) is 6.
On the other hand, the $x$-coordinate of A is -2, so the horizontal length of △AOP is 2. The $x$-coordinate of B is 6, so the horizontal length of △BOP is 6. Therefore, we can get the area of each as follows.
- The area of △AOP: $6×2×\displaystyle\frac{1}{2}=6$
- The area of △BOP: $6×6×\displaystyle\frac{1}{2}=18$
Adding the area of each triangle gives the answer as follows.
- $△AOB=6+18=24$
(d)
If there is a point D on (1), △COD is as follows.
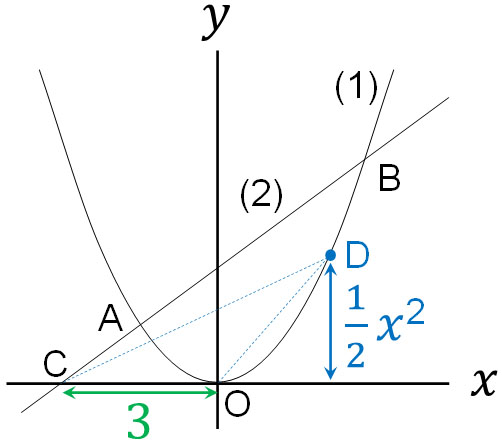
The linear function in (2) is $y=2x+6$. Therefore, the intersection with the $x$-axis can be calculated by substituting $y=0$ as follows.
$0=2x+6$
$-2x=6$
$x=-3$
The coordinate of point C is $(-3,0)$. In other words, the length of CO is 3. On the other hand, what is the vertical length of △COD? The quadratic function in (1) is $y=\displaystyle\frac{1}{2}x^2$. So the coordinate of point D is $(x,\displaystyle\frac{1}{2}x^2)$. In other words, the vertical length is $\displaystyle\frac{1}{2}x^2$.
The area of the COD is 27. Substituting in the formula for the area of a triangle, we can calculate it as follows.
$3×\displaystyle\frac{1}{2}x^2×\displaystyle\frac{1}{2}=27$
$x^2=27×\displaystyle\frac{4}{3}$
$x^2=36$
$x=-6,x=6$
Thus, when $x=-6$ or $x=6$, the area of △COD is 27.
Read Quadratic Graphs and Solve Equations
The quadratic functions we learn in mathematics are similar in nature to linear functions. However, there are a lot of things to remember, and you need to understand the concept of a parabola.
Also, when solving quadratic function problems, you will not necessarily be asked only about quadratic functions. It is often a complex problem that includes linear equations, simultaneous equations, linear functions, and graphs. So try to use the properties of quadratic functions to solve the problems.
What is especially important in quadratic functions is the value of $a$ and the rate of change. Depending on the value of $a$, the shape of the graph varies. Also, by calculating the rate of change, we can get the slope of the line passing through the two coordinates.
Many natural phenomena in the world involve quadratic functions. Learn the properties of quadratic functions and try to understand how to draw graphs and solve problems.