A genre studied in mathematics is similarity. Similarity is frequently given as a problem in figures. In similarity problems, there are proof problems and calculation problems.
Therefore, we need to learn the conditions under which figures are similar. Not only that, but you should be able to find the side lengths using similar figures. In this case, we can use proportional relationships.
Proportions are used frequently in our lives. Therefore, proportional calculations are important, and in calculation problems using similar figures, you will be able to calculate the side lengths by considering them in the same way as proportions. You can also calculate the area ratio and volume ratio from the side lengths.
You can solve problems by finding similar figures and checking the ratio of the side lengths. Therefore, in order to understand the similarity of figures, we will explain the characteristics of similar figures, the similarity theorem, and the similarity ratio.
Table of Contents
What Is The Difference Between Congruence and Similarity: Properties of Similarity
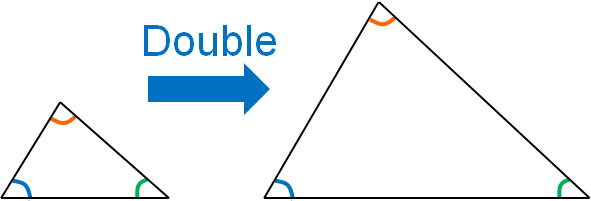
In mathematics, we study congruence. There is a difference between congruence and similarity. Congruence refers to shapes that are exactly the same. On the other hand, figures that are the same in shape but different in size are called similarity.
For example, the following figures have a similarity relationship.
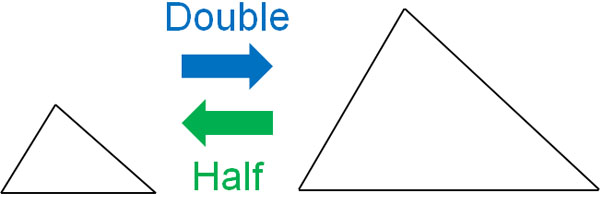
The shapes of the figures are the same. However, they are different in size. Understand that a similar shape is one in which the side lengths are larger or smaller. Also, similarity has the following properties.
-The Corresponding Side Length Ratios Are Equal
Since the figures are enlarged or reduced, the side length ratio of each similar figure is the same. For example, if one side is doubled in length, all the other sides will also be doubled.
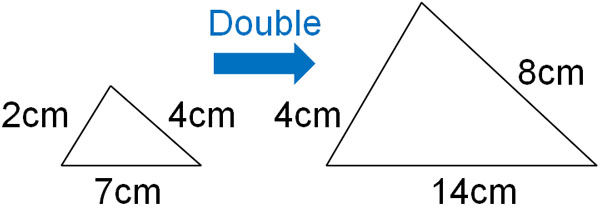
If the figures are similar and the side ratio is known, the other side lengths can be calculated.
-The Sizes of the Corresponding Angles Are Equal
For the side lengths, all ratios are equal for similar figures, as mentioned above. On the other hand, for angles, they are the same for all pairs of angles. For example, we have the following.
If the angles are different, the shape of the figure will change. Therefore, they are not similar shapes. In the case of similarity, the angles are always the same, and the only difference is the side lengths.
-The Sign Used in Similarity
In addition, the symbol ∼ is used in similarity. For example, write △ABC∼△EDF. In this case, △ABC and △EDF are similar.
For congruence, we use the ≅ symbol. In the same way, remember to use a special symbol for similarity.
Three Conditions for Triangles to Be Similar
When do triangles have similarities? There are three similarity theorems for triangles in total. Here are the similarity conditions for triangles.
- Side – Side – Side (SSS) Similarity Theorem
- Side – Angle – Side (SAS) Similarity Theorem
- Angle – Angle (AA) Similarity Theorem
The details of each are as follows.
-Side – Side – Side (SSS) Similarity Theorem
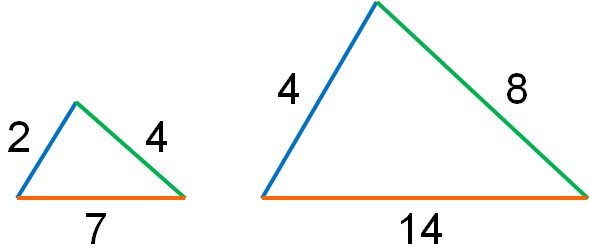
If the ratios of three pairs of sides are all equal, they are similar.
-Side – Angle – Side (SAS) Similarity Theorem
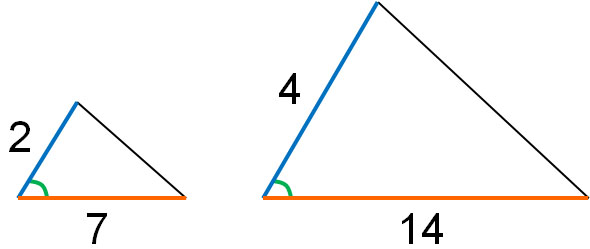
If the side length ratios of the two pairs are equal and the angle between the sides is the same, the two figures are similar.
-Angle – Angle (AA) Similarity Theorem
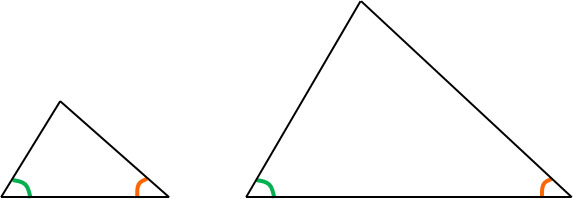
If two pairs of angles are equal, then each shape is similar.
Note that in most cases, we use Angle – Angle (AA) to prove the similarity of figures. It is rare to use Side – Side – Side (SSS) or Side – Angle – Side (SAS) to prove the similarity of triangles.
Therefore, in similarity problems, we first consider Angle – Angle (AA). Try to find triangles that are similar by looking for two sets of the same angles. After that, you can use the similarity theorem to prove that the triangles are similar.
Relationship Between Similarity Ratios and Side Lengths
In similarity figures, it is important not only to prove that the figures are similar to each other but also to use the similarity to calculate the side lengths. The calculation used is the similarity ratio. What is a similarity ratio?
Similarity ratios should be understood as ratios of the side lengths. In similar figures, the ratios of the corresponding side lengths are the same. For example, in the following case, the similarity ratio is 1:3.
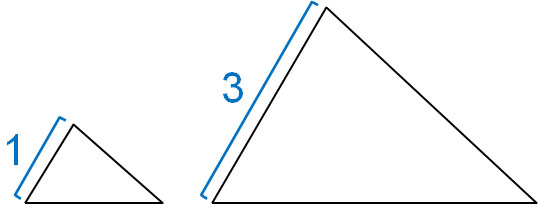
If the side length ratio is 1:3, the similarity ratio of the two triangles is 1:3.
-The Similarity Ratio Can Be Used Not Only for Side Lengths But Also for Heights
Depending on the similarity ratio, the side lengths will change. The same can be said for the height as well as the side length. For example, if the similarity ratio is 1:3, not only will all the side lengths be tripled, but the height will also be tripled, as shown below.
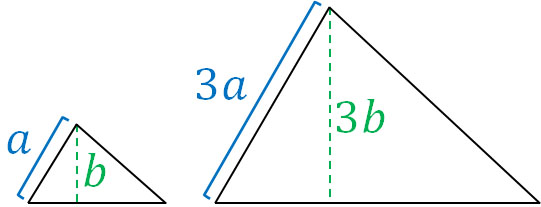
In similarity figures, all lengths are related to the similarity ratio.
Calculating the Side Lengths Using the Proportional Relationships
Once you understand the similarity ratio, you can calculate the side lengths. The calculation method is the same as for proportions. For example, if we have the following similarity figure (△ABC∼△EDC), what is the length of a?
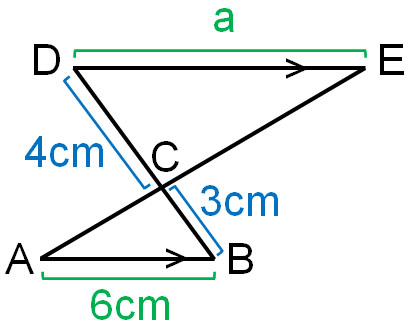
The length of the BC is 3 cm, and the length of the DC is 4 cm. Therefore, we know that the similarity ratio is 3:4.
By using this similarity ratio, let’s find the length of a. The length of AB is 6 cm. Therefore, by using the similarity ratio, we can create the following proportional relationship.
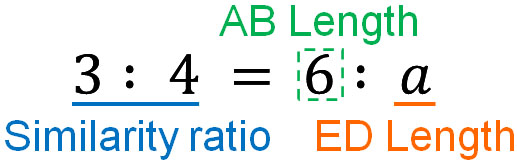
Proportional relationships can be calculated by outer multiplication and inner multiplication. The previous proportional relationship can be calculated as follows.
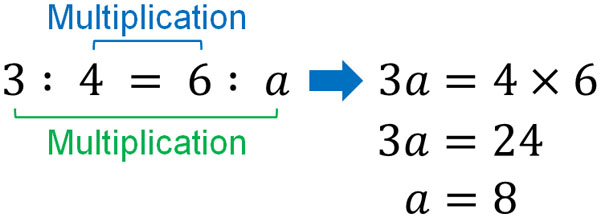
After creating a proportional relationship, be sure to remember the properties that can be calculated by outer multiplication and inner multiplication. Proportional relationships are used in many aspects of mathematics, not just similarity.
For reference, we can see that the following proportional relationships all have the same value when multiplying outside and inside.
- $1:3=3:9$
- $2:5=6:15$
- $4:3=6:\displaystyle\frac{9}{2}$
When the proportions are the same, the numbers will always match when multiplying outside and inside. Using this property of proportional relationships, we can calculate the side lengths of similar figures.
The Area Ratio Is Squared, and the Volume Ratio Is Cubed
The side lengths can be calculated by using similarity ratios in this way. However, in similarity problems, you may be asked to calculate the area and volume. Therefore, it is necessary to understand how to calculate the area ratio and volume ratio.
In the case of the area ratio, it is the square of the similarity ratio. For example, if the similarity ratio is 1:2, the area ratio is 1:4 (22). And if the similarity ratio is 1:3, the area ratio is 1:9 (32). Why is it that the square of the similarity ratio becomes the area ratio?
When calculating the area of a triangle, you can use the following formula.
- Triangle area = vertical × horizontal × $\displaystyle\frac{1}{2}$
As mentioned above, if the similarity ratio is doubled or tripled, the side lengths will be doubled or tripled. The area is calculated by multiplying the vertical and horizontal lengths. This is why the area ratio is the square of the similarity ratio.
For example, if the similarity ratio is 1:2, the vertical and horizontal lengths are doubled, and the area ratio is quadrupled because two doubled sides are multiplied. In the case of a 1:3 similarity ratio, the vertical and horizontal lengths are tripled, and the area ratio is 9 times because two tripled sides are multiplied.
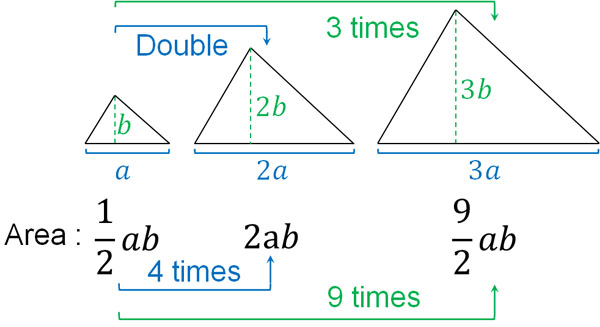
On the other hand, what about volume? The volume is calculated by the following formula.
- Volume = Length × Width × Height
In a similar figure, if the length is doubled, the width and height are also doubled. Therefore, the volume is the cube of the similarity ratio.
For example, if the similarity ratio is 1:2, the length, width, and height are each doubled. Three doubled sides are multiplied, so the volume ratio is 8 times (23 times). If the similarity ratio is 1:3, the length, width, and height are each tripled. Three tripled sides are multiplied, so the volume ratio is 27 times (33 times).
Exercise: Proof of Similarity and Calculation of Similarity Ratio
Q1: Solve the following problem.
There is a trapezoid ABCD with AD||BC, and the intersection point of AC and BD is O. AD is 3 cm, BC is 9 cm, and the area of △OAD is 12 cm2.
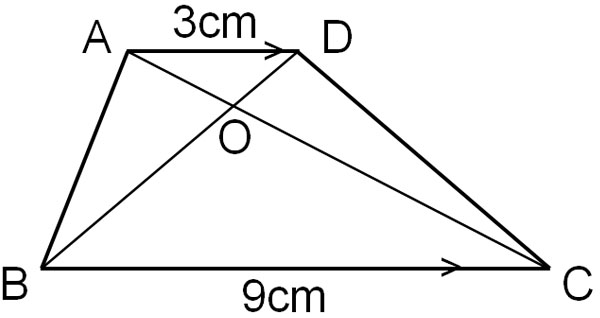
- Prove that △OAD∼△OCB
- Calculate the area of △OCB
- Calculate the area of the trapezoid ABCD
A1: Answers.
(a)
- In △OAD and △OCB
- ∠AOD = ∠COB: Vertical Angles are equal – (1)
- ∠OAD = ∠OCB: Alternate angles in parallel lines are equal – (2)
- From (1) and (2), since Angle – Angle (AA), △OAD∼△OCB
(b)
Since AD = 3 cm and BC = 9 cm, the similarity ratio is 1:3. The area ratio is the square of the similarity ratio. In other words, the area ratio is 1:9. Since the area of △OAD is 12cm2, we can create the following proportional relationship.
- $1:9=12:x$
Solving this proportional relationship, we get the following.
- $x=9×12=108$
Therefore, the area of △OCB is 108 cm2.
(c)
We have found the area of △OAD and △OCB. On the other hand, how can we calculate the area of △OAB and △ODC? If we know the areas of these triangles, we can add all the triangles to get the area of the trapezoid.
It may seem difficult to find the area of △OAB and △ODC. On the other hand, it is possible to calculate the area of △ABC and △DBC. The similarity ratio between △OAD and △OCB is 1:3, so the height ratio between △ABC and △OCB is 4:3, as shown below. In the same way, the ratio of the heights of △DBC and △OCB is 4:3.
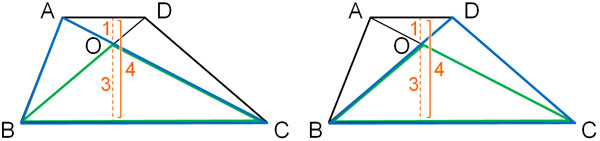
The base BC of the triangles is the same. The only difference is the height. Also, as the height increases, the area increases in proportion to the ratio. So by using the ratio of the heights, we can create the following proportional relationship.
- $4:3=x:108$
Solving this proportional relationship, we get the following.
- $3x=4×108$
- $x=144$
Therefore, the area of △ABC is 144cm2. Subtracting the area of △OCB from this, we can get the area of △OAB. Therefore, the area of △OAB is 36cm2.
- $△OAB=144-108=36$
The base and height lengths of △ABC and △DBC are the same. Also, by subtracting the area of △OCB, we can get the area. Therefore, the areas of △OAB and △ODC are the same.
Then, adding the areas of all the triangles, we find that the trapezoid area is 192 cm2.
- $12+108+36+36=132$
Using the Similarity Theorems to Solve Problems
Compared to the proof of congruence, the proof of similarity is easy: if you find that two pairs of angles are equal, then the two triangles are similar.
However, in similarity figures, we rarely end up proving that they are similar. Furthermore, we need to solve advanced problems. By using the similarity ratio, we can calculate the side lengths.
In addition to the side lengths, you may also have to calculate the area and volume. In such cases, we need to use similarity ratios to find the area and volume ratios.
In similarity figures, you need to be able to solve advanced problems by using ratios. So let’s review how to calculate proportional relationships and make sure that you can even calculate area and volume.