A field we learn about in mathematics is a square root. The square root allows us to represent numbers before they are squared.
Square root calculations include addition and subtraction. For multiplication and division, we can just multiply the numbers in the root symbol. For addition and subtraction, on the other hand, the rule is that the numbers in the radical symbol must be the same in order to calculate.
Also, in addition and subtraction, you need to perform prime factorization and rationalize the denominator. In the calculation of square roots, addition and subtraction are more difficult than multiplication.
So we will explain how to add and subtract square roots.
Table of Contents
How to Add and Subtract Square Root
In square root multiplication and division, we can multiply the square roots by each other. Although there are some precautions to be taken, all you have to do is multiply the numbers in the root symbol.
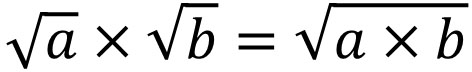
On the other hand, how should we think about addition and subtraction? For addition and subtraction, you should not add or subtract square roots that have different numbers. For example, the following is wrong.

The method of calculation is different from multiplication and division. Why can’t we add the square roots of different numbers to each other? Because a square root is a number before it is squared, so it has different properties from integers.
For example, $\sqrt{9}=\sqrt{3^2}=3$. And $\sqrt{16}=\sqrt{4^2}=4$. In this case, we have the following.
- $\sqrt{9}+\sqrt{16}=3+4=7$
On the other hand, what happens if we add the numbers in the radical symbols without making them integers? The result is as follows.
- $\sqrt{9}+\sqrt{16}=\textcolor{red}{\sqrt{9+16}}=\sqrt{25}$
52 is 25. Therefore, $\sqrt{25}=\sqrt{5^2}=5$. However, the actual answer must be 7. So, $\sqrt{9}+\sqrt{16}=\sqrt{25}=5$ is wrong.
Since the squared number is the square root, we get the following.
- $\sqrt{36}=6$
- $\sqrt{100}=10$
- $\sqrt{2500}=50$
- $\sqrt{10000}=100$
As you can see, the numbers in the root sign are much larger than the integers. Think of integers (natural numbers) and numbers in the radical symbol are completely different. This is why adding or subtracting directly to the numbers in the root sign is a mistake.
Addition and subtraction Can Be Done If the Numbers in a Radical Symbol Are the Same
How can we add and subtract with square roots? You can only add and subtract if the numbers in the root symbol are the same. For example, it is the following.
- $4\sqrt{2}-\sqrt{2}=3\sqrt{2}$
In this case, the number in the radical sign is common to 2. Therefore, it is possible to add and subtract the integers in front of the root sign.
$4\sqrt{2}$ means that there are four $\sqrt{2}$. So if we subtract one $\sqrt{2}$, we have three $\sqrt{2}$ left.

This is why if the numbers in the root sign are the same, we can add and subtract.
On the other hand, what happens if the numbers in the root symbol are different? As we already explained, if the numbers in the radical symbol are the same, we can add and subtract. However, if the numbers in the radical symbol are different, we cannot add or subtract them. For example, the calculation is as follows.
- $2\sqrt{\textcolor{red}{2}}-\sqrt{3}+3\sqrt{\textcolor{red}{2}}=5\sqrt{2}-\sqrt{3}$
We cannot add or subtract numbers with different properties. Therefore, the answer to this calculation is $5\sqrt{2}-\sqrt{3}$. To distinguish if addition and subtraction are possible, see if the numbers in the root symbol are the same or not.
-The Calculation Method is the same as the Algebraic Expression
Square roots are calculated in the same way as in algebraic expressions. In algebraic expressions, even different alphabets can be multiplied and divided. However, different letters cannot be added or subtracted, as shown below.
- $2x+x-2y+4y=3x+2y$
Square roots can also be multiplied and divided, even if the numbers in the root symbol are different. However, if the numbers in the radical sign are different, we cannot add or subtract, as shown below.
- $2\sqrt{\textcolor{red}{2}}+\sqrt{\textcolor{red}{2}}-2\sqrt{\textcolor{blue}{3}}+4\sqrt{\textcolor{blue}{3}}=3\sqrt{2}+2\sqrt{3}$
Even if the properties are different, we can still do multiplication and division. But if they are different in properties, we cannot add or subtract. In mathematics, make sure to understand this rule.
Match the Numbers in the Root Symbol by Prime Factorization
Once you understand the rules we’ve discussed, you will be able to add and subtract square roots. However, before adding and subtracting, in many cases, we must do prime factorization beforehand. By doing prime factorization, the numbers in the radical sign become clearer.
When calculating the square root, we must do prime factorization to make $a\sqrt{b}$. For example, we have the following.
$\sqrt{18}+\sqrt{50}-\sqrt{32}$
$=\sqrt{3^2×2}+\sqrt{5^2×2}-\sqrt{4^2×2}$
$=3\sqrt{2}+5\sqrt{2}-4\sqrt{2}$
$=4\sqrt{2}$
Prime factorization is important in the calculation of square roots because it allows us to minimize the number in the radical sign. As a result, addition and subtraction are available.
After Rationalizing the Denominator, Make a Common Denominator and Calculate It
There is another important procedure when doing the square root calculation. It is rationalizing the denominator. If the denominator has square roots (irrational numbers), it cannot be calculated. So, by rationalizing the denominator, if we change the number in denominators to integers, we can add and subtract square roots by creating a common denominator.
For example, how can we do the following calculation?
- $\displaystyle\frac{1}{\sqrt{3}}+\sqrt{3}$
In mathematics, the answer is incorrect if the denominator has a root sign. The reason for this is that rationalizing the denominator allows us to make the numbers simpler.
In the case of rationalizing the denominator, we can calculate the following.
$\displaystyle\frac{1}{\sqrt{3}}+\sqrt{3}$
$=\displaystyle\frac{1\textcolor{red}{×\sqrt{3}}}{\sqrt{3}\textcolor{red}{×\sqrt{3}}}+\sqrt{3}$
$=\displaystyle\frac{\sqrt{3}}{3}+\sqrt{3}$
$=\displaystyle\frac{\sqrt{3}}{3}+\textcolor{red}{\displaystyle\frac{3\sqrt{3}}{3}}$ (Create a common denominator)
$=\displaystyle\frac{4\sqrt{3}}{3}$
Rationalizing the denominator in this way allows you to add or subtract with a common denominator.
Square Root Multiplication and Division Using the Distributive Property
When we actually do square root calculations, we don’t just add and subtract. In many cases, the equation includes multiplication and division. Therefore, we should be able to calculate expressions that include a mixture of addition, subtraction, multiplication, and division.
As mentioned earlier, algebraic expressions and square roots are calculated in the same way. An important rule in algebraic expressions is the distributive property. The following is the distributive property.
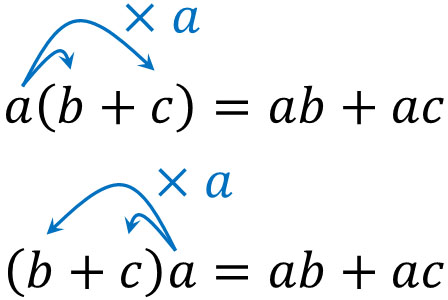
The distributive property is a method for removing the parentheses when multiplying. We should use the distributive property to calculate the square root as well.
For example, how can we calculate the following?
- $2(1+\sqrt{2})$
To solve this problem, let’s use the distributive property. It looks like the following.
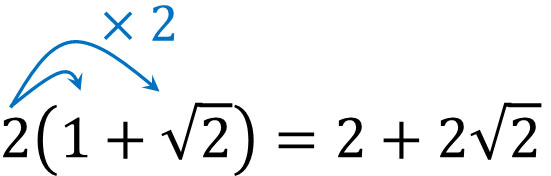
After expanding the equation, proceed with the calculation by adding and subtracting.
Expanding the Equation with the Factoring Formulas
However, in calculating square roots, we have to calculate more complicated expressions. We use the factoring formulas to expand the expression.
When expanding a multiplication equation with two parentheses, we use the following formula.
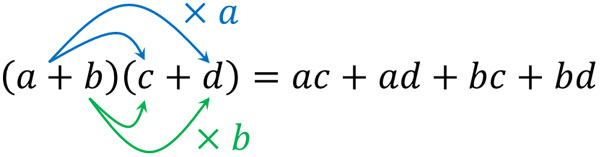
Other factoring formulas are also used when calculating more efficiently. The following four formulas must be remembered in mathematical calculations.
- $(x+a)(x+b)=x^2+(a+b)x+ab$
- $(x+a)^2=x^2+2ax+a^2$
- $(x-a)^2=x^2-2ax+a^2$
- $(x+a)(x-a)=x^2-a^2$
By using these formulas, we can calculate the square root. For example, let’s consider how we can do the following calculation.
- $(3+\sqrt{5})^2$
In order to do this calculation, we must use the factoring formula. The calculation is as follows.
$(3+\sqrt{5})^2$
$=3^2+2×3×\sqrt{5}+(\sqrt{5})^2$
$=9+6\sqrt{5}+5$
$=14+6\sqrt{5}$
Integers and square roots are different in properties. Therefore, 14 and $6\sqrt{5}$ cannot be calculated further. So, the calculation is complete. Let’s try to understand the properties of square roots so that we can calculate them.
Exercises: Addition and Subtraction of Square Root Calculation
Q1: Do the following calculations.
- $\sqrt{75}+\sqrt{98}-\sqrt{108}$
- $\sqrt{8}-\displaystyle\frac{1}{\sqrt{2}}$
- $\sqrt{6}(\sqrt{2}-\sqrt{3})+3\sqrt{3}$
A1: Answers.
(a)
After doing prime factorization, let’s do the square root calculation.
$\sqrt{75}+\sqrt{98}-\sqrt{108}$
$=5\sqrt{3}+7\sqrt{2}-6\sqrt{3}$
$=7\sqrt{2}-\sqrt{3}$
(b)
After rationalizing the denominator, let’s do the square root calculation.
$\sqrt{8}-\displaystyle\frac{1}{\sqrt{2}}$
$=2\sqrt{2}-\displaystyle\frac{1\textcolor{red}{×\sqrt{2}}}{\sqrt{2}\textcolor{red}{×\sqrt{2}}}$
$=2\sqrt{2}-\displaystyle\frac{\sqrt{2}}{2}$
$=\displaystyle\frac{4\sqrt{2}}{2}-\displaystyle\frac{\sqrt{2}}{2}$
$=\displaystyle\frac{3\sqrt{2}}{2}$
(c)
Let’s calculate using the distributive property.
$\sqrt{6}(\sqrt{2}-\sqrt{3})+3\sqrt{3}$
$=\sqrt{12}-\sqrt{18}+3\sqrt{3}$
$=2\sqrt{3}-3\sqrt{2}+3\sqrt{3}$
$=-3\sqrt{2}+5\sqrt{3}$
Q2: Do the following calculation.
When $x=2+\sqrt{2}$ and $y=4+2\sqrt{2}$, calculate the value of $xy-2x^2$.
A2: Answer.
You can substitute numbers for $x$ and $y$ to calculate them. The result is as follows.
- $(2+\sqrt{2})(4+2\sqrt{2})-2(2+\sqrt{2})^2$
However, it is hard to calculate. Isn’t there an easier way to calculate it? So, let’s use factorization. Factoring $xy-2x^2$ gives us the following.
- $xy-2x^2=x(y-2x)$
Then substitute into this equation. It is as follows.
$x(y-2x)$
$=(2+\sqrt{2})[4+2\sqrt{2}-2(2+\sqrt{2})]$
$=(2+\sqrt{2})(4+2\sqrt{2}-4-2\sqrt{2})$
$=(2+\sqrt{2})×0$
$=0$
Adding and Subtracting Square Root in Mathematics
When we learn the basics of square roots, after learning multiplication and division, we learn addition and subtraction. You can’t add the numbers in the root symbol; there are rules for square root calculation.
Adding and subtracting square root is the same as calculating an algebraic expression. For multiplication and division, we can multiply without thinking. On the other hand, if we want to find the answer to addition and subtraction, the numbers in the radical sign must be the same. If they are not the same in properties, you cannot add or subtract them.
Therefore, we need to do prime factorization and rationalize the denominator so that the numbers in the root symbol are matched. Also, try to use factoring formulas for multiplication equations with parentheses.
When learning square roots, one of the most difficult concepts to learn is addition and subtraction. Make sure you understand why we cannot add and subtract unless the numbers in the root symbol are the same before calculating square roots.