When you learn math, you have to understand negative numbers. Unlike when you were learning only positive integers, learning the concept of zero and addition and subtraction will allow you to perform complex calculations.
It may seem strange to you that there are numbers less than zero. However, we use negative numbers in many aspects of our daily lives. Therefore, it is very important to use negative integers as well as positive integers for calculations.
So what is the concept of 0 and negative numbers? How can we think and calculate positive and negative numbers?
When learning mathematics, we all need to understand positive and negative numbers. We will explain how to calculate positive and negative integers, with some exercises.
Table of Contents
0 (Zero) Is Used to Indicate a Criteria
In general, 0 (zero) indicates that there is nothing. For example, if you have \$1, and if you spend it, the money you have is \$0.
If non-existence means zero, the concept of a negative doesn’t make sense. When learning about negative integers, many people get confused because they may think that there are numbers that are smaller than non-existent ones.
However, 0 does not just indicate that it does not exist. It has other meanings as well. It is a criterion. By using zero as a standard, we use positive and negative numbers, depending on whether the number is greater or less than zero.
For example, we use temperature in our daily lives. Temperature has a standard of 0°C (32°F). If the temperature is lower than 0°C, the number is negative. In a city where it snows, many people will experience negative temperatures.

Given this fact, we can realize that it’s not strange to use negative numbers as well as positive numbers; since zero has a meaning of indicating a standard, many people use negative numbers in their daily lives.
Positive Integers (Natural Numbers) and Negative Integers Indicate Increase or Decrease from a Reference
Once you learn that zero has the concept of a standard, you will understand what a positive and negative integer means. Positive integers (natural numbers) and negative integers indicate how far away they are from the reference point (0).
In the following figure, with zero as the reference point, the numbers to the right are positive integers (natural numbers).

On the other hand, numbers to the left of zero are negative integers. By using plus and minus, we can express an increase or decrease from a standard.
For example, let’s consider losing weight by going on a diet. In that case, the majority of people use their current weight as a reference point (zero). If you have lost 3kg of weight, then you can say that you have successfully gained -3kg of weight.
-You Can Replace Plus and Minus
Therefore, the number of pluses and minuses can be replaced. For example, the following have the same meaning.
- I’ve lost 3kg of weight.
- I’ve gained -3kg of weight.
Also, the following have the same meaning
- The temperature drops by 5°C.
- The temperature goes up by -5°C.
It is important to understand that these rephrases are possible when learning positive and negative numbers.
How to Distinguish Between Large and Small Numbers, and Absolute Value
With positive and negative numbers, how can we distinguish between large and small numbers? In order to understand this, we need to understand the concept of absolute value.
We have understood that we can check positive and negative numbers based on zero. For large and small numbers, check how far they are from zero. Regardless of whether it is positive or negative, the absolute value is how far it is from zero.
For example, the absolute value of 4 is 4. On the other hand, the absolute value of -3 is 3. If we go three to the left from 0, we get -3. Since the distance from 0 is 3, the absolute value of -3 is 3.

Once we learn this concept, we will be able to distinguish between large and small numbers. For example, with 5 and 3, we can see that 5 is a larger number than 3. Therefore, we can express 5>3. On the other hand, which number is larger, -3 or -5?
The absolute value of -3 is 3. Also, the absolute value of -5 is 5. The important fact is that the larger the number (absolute value) of a negative number, the smaller the number becomes. The absolute value of -5 is greater than -3. Therefore, -3 is a larger number and can be expressed as $-3>-5$.

It may seem strange that even though the number is large, the minus sign makes it a small number. However, we also use this in our daily lives.
For example, between -3°C (26.6°F) and -20°C (-4°F), -20°C is colder. This is because -20°C is a larger negative number. Understand that even though the number (absolute value) is large, it will be a small number in a negative number.
Addition and Subtraction of Positive Numbers
Understanding the concepts of zero and negative numbers will help you understand addition and subtraction for positive and negative numbers.
It is easy to understand positive and negative numbers if you learn about them from addition and subtraction of positive numbers. When dealing with positive numbers, there are two types.
- Addition of positive numbers
- Subtraction of positive numbers
We will explain each of these.
Using Parentheses in Addition of Positive Numbers
You have already learned about the addition of positive numbers in elementary school math. Therefore, you will be able to understand the addition of positive numbers to positive numbers without any difficulty. For example, the following calculation is easy.
- $3+1=4$
In this case, $3+1$ can also be expressed as follows.
- $3+(+1)$
- $(+3)+(+1)$
They all have the same meaning. In addition, you can use two +’s in a row. However, instead of writing ++, we use parentheses.
-Add a Positive Number to a Negative Number
How can we add a positive number to a negative number? For example, the following calculation.
- $-5+3$
It can also be expressed as $-5+(+3)$ or $(-5)+(+3)$. In any case, this calculation requires adding 3 to -5. In other words, you have to answer a number that is 3 greater than -5.
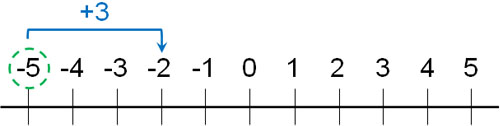
The absolute value of -5 is 5. By doing +3 to -5, we can go three steps to the right and get -2. Therefore, the answer is -2.
Rules for Subtracting Positive Numbers
In contrast, how can we think about subtraction of positive numbers? For example, suppose we have the following calculation
- $3-2=1$
We have already learned about this calculation in elementary school. The important thing is that it can be replaced by the following equations.
- $3-(+2)=1$
- $(+3)-(+2)=1$
All positive numbers have a + hidden in them. For example, when we use the number 2 or 3, we can represent it as +2 or +3. For positive integers (natural numbers), the + can be omitted. Just to describe it in detail, $3-2$ can be represented as $3-(+2)$.
-Subtract a Positive number from a Negative number
Of course, it is common to subtract positive numbers (natural numbers) from negative numbers. For example, what is the answer to the following calculation?
- $-1-3$
This equation can also be replaced with $-1-(+3)$ or $(-1)-(+3)$. In order to subtract +3 from -1, the answer must be a number that is 3 less than -1.
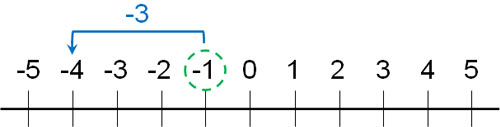
Therefore, the answer is -4.
- $-1-3=-4$
- $-1-(+3)=-4$
- $(-1)-(+3)=-4$
It is calculated like this.
Addition and Subtraction of Negative Numbers
We’ve discussed positive numbers, and it’s not difficult to understand addition and subtraction for positive numbers. It is the addition and subtraction of negative numbers that are difficult.
- Adding the negative numbers
- subtract the negative numbers
What do these mean? For example, when we calculate $1 – (-3)$, we get the following.
- $1-(-3)=1+3=4$
Many people try to learn how to calculate without understanding why. However, you have to understand the reason. So, we will explain including the reasons.
Learn How to Add Negative Numbers by Replacing
Calculations involving the addition of negative numbers are frequently given. For example, how do we think about the following calculation?
- $2+(-4)$
As mentioned above, the numbers can be rephrased. For example, if you lose 2kg of weight, you can rephrase it as “I’ve gained -2kg of weight”. Even though it is expressed as an increase in weight, it is a -2 kg plus, so you have lost weight.
In this way, you can replace the positive with the negative. In other words, we can rephrase it as follows.
- $2-4$:4 less.
- $2+(-4)$: -4 higher
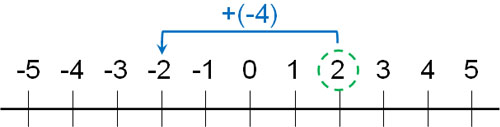
Subtract 4 from 2 is -2. A number 4 less than 2 is -2. Understand that adding a negative number is, in essence, the same as subtracting a positive number.
Why Negative Subtraction Is Positive?
When it comes to understanding negative numbers, it is the subtraction of negative numbers that confuses many people. What we have explained so far are the following.
- Addition of positive numbers (positive integers)
- Subtraction of positive numbers (positive integers)
- Addition of negative numbers (negative integers)
Addition and subtraction of positive numbers are already taught in elementary school. Also, the addition of negative numbers can be rephrased as the subtraction of positive numbers (natural numbers). On the other hand, how can we calculate the following, for example?
- $2-(-3)$
We can also rephrase this calculation. The minus sign has the opposite meaning. As mentioned above, the expression “I’ve lost 2kg” can be reworded as “I’ve gained -2kg”.
So, how should we think about the expression “I lost -3kg”? Since minus has the opposite property, -3kg decreased means 3kg increased. The minus of a minus is a plus.
That’s why when you subtract a negative number, you can change it to a positive number.
- $2-(-3)=2+3=5$

It is important to note that minus has the opposite meaning. A lot of people don’t understand in mathematics why subtracting a negative value means a positive value. Once you understand that a negative has the opposite meaning and can be rephrased, you will understand this reason.
Exercises: Addition and Subtraction of Positive and Negative Numbers
Q1: Express the size of the following numbers using the inequality sign.
- $-2、4、-3$
- $-0.3、-3、0$
A1: Answers.
For negative numbers, the higher the number (absolute value), the smaller the number. Since the concept is the opposite of positive numbers, the order of inequality is as follows.
- $4>-2>-3$
- $0>-0.3>-3$
For example, in (b), when comparing 0, 0.3 and 3, the order of the higher numbers is $3>0.3>0$. For a negative number, the opposite is true, the higher the number (absolute value), the smaller it is, so $0>-0.3>-3$.
Q2: Do the following calculation.
- $7-(+3)$
- $-0.5+(-0.2)$
- $-3-(-6)$
- $\displaystyle\frac{1}{2}-\left(-\displaystyle\frac{1}{3}\right)$
- $-3 +(-2)-(-6)-5$
A2: Answers.
In calculating positive and negative numbers, let’s rephrase them. In both junior high school math and high school math, everyone calculates after replacing signs. The point of substitution is as follows.
- $+$ and $+$ becomes $+$
- $+$ and $-$ becomes $-$
- $-$ and $+$ becomes $-$
- $-$ and $-$ becomes $+$
All addition and subtraction can be rephrased in this way, including decimals and fractions. Therefore, we can calculate as follows.
(a)
$7-(+3)=7-3=4$
(b)
$-0.5+(-0.2)=-0.5-0.2=-0.7$
(c)
$-3-(-6)=-3+6=3$
(d)
$\displaystyle\frac{1}{2}-\left(-\displaystyle\frac{1}{3}\right)$
$=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}$
$=\displaystyle\frac{3}{6}+\displaystyle\frac{2}{6}=\displaystyle\frac{5}{6}$
(e)
$-3+(-2)-(-6)-5$
$=-3-2+6-5=-4$
You cannot solve a problem without rephrasing the pluses and minuses. Make sure you know whether you are adding or subtracting. If you change the signs, it is elementary school arithmetic content, so all you have to do is add and subtract.
Fractions are a little more complicated because you need to reword the signs and then adjust the denominator. However, calculating fractions should be taught in elementary school, so it is not difficult.
Q3: Do the following calculations.
The table below shows how many centimeters taller the four people in A to D are from 160 cm.
| A | B | C | D | |
| Difference from 160 cm (cm) | 12 | -4 | 7 | -9 |
- How many centimeters taller would the tallest person be than the shortest person?
- Find the average height of the four people.
A3: Answers.
a. How many centimeters taller would the tallest person be than the shortest person?
The tallest person is A. And the shortest person is D. A is +12 cm taller and D is 9 cm shorter.
When calculating the difference between the numbers, you have to subtract. For example, according to the diagram above, A is +12 cm tall and C is +7 cm tall; the difference in height between A and C is $12cm-(+7cm)=12cm-7cm=5cm$. In the same way, we use subtraction in comparing numbers.
The height difference between A and D is calculated as follows.
- $12-(-9)=12+9=21cm$
Therefore, the tallest person is 21 cm taller than the shortest person.
b. Find the average height of the four people.
When calculating the average height, one way to calculate the average height is to calculate the respective heights from A to D. If you calculate the height of each of them, you will get the following
| A | B | C | D | |
| Height (cm) | 172 cm | 156 cm | 167 cm | 151 cm |
After adding the heights from A to D, you can divide the heights by four to get the average of the heights. But can’t we find the average in an easier way?
In this regard, let’s try to calculate how much it differs from the average value. As shown below, the heights of the four people are different.
- A: +12 cm
- B: -4 cm
- C: 7 cm
- D: -9 cm
What is the average height difference between the four people? If you add up the height difference between the four people, it is as follows.
$12+(-4)+7+(-9)$
$=12-4+7-9=6cm$
The total difference in height between the 4 people is 6 cm. If you divide the total by the number of people, you can calculate the average value. In other words, we can get the average value of how many cm taller (or shorter) each person is from 160 cm.
If you divide 6 cm (total value) by 4 people, you get $6÷4=1.5cm$. This means that the average height of the 4 people is +1.5 cm taller than 160 cm. Therefore, the average height of the 4 people is 161.5 cm.
- $160+1.5=161.5$
Use Positive and Negative Numbers to Add and Subtract
When learning negative numbers, many people are confused; they don’t understand why there are values lower than 0 (zero). Also, most people, even adults, cannot explain why subtraction of a negative number becomes a positive number.
However, as we’ve explained, we find that we use negative numbers in many situations, including in daily lives. 0 means a standard value, and the absolute value is used to compare the size of a number.
In addition, when we actually use plus and minus numbers to add and subtract, we often use parentheses. In calculations that use parentheses, it is always possible to replace signs. Even when solving difficult problems in high school and college, everyone uses replacement, so be sure to do the calculation after the replacement.
Once you learn these rules, you will be able to solve addition and subtraction problems with positive integers (natural numbers) and negative integers. The method is the same for decimals and fractions. Many people have a hard time solving problems with negative subtraction in particular, so make sure you understand including the reasons why.





