Decimals are taught in elementary school mathematics. After learning multiplication with decimals, you need to be able to do division.
When calculating decimals, a division is a bit more complicated. This is because it is not always divisible. You have to calculate until you can divide or use the remainder to get the answer. It is also common to move the decimal point.
When it comes to calculating decimals, addition, subtraction, and multiplication are easy. Division, on the other hand, requires a lot of understanding. In this section, we will explain how to do decimal division.
Table of Contents
How to Divide Using Decimals and Integers: The Case of Divisible Numbers
Let’s start with the simple division of decimals. As long as the numbers are divisible, the calculations are not complicated. For example, how do you calculate the following?
- $24.22÷7$
When doing this calculation, create the following long division.
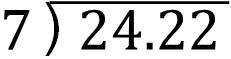
The way to do division is the same as a long division with whole numbers. Ignore the decimal point and perform the division calculation. Then, add the decimal point to the answer (quotient) in the same position. The result is as follows.
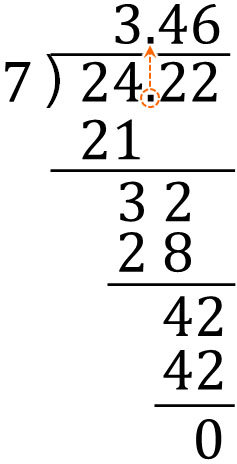
When doing division using decimals and integers, it is not difficult to calculate as long as the numbers are divisible. After dividing, add the decimal point in the same place.
In some calculation problems, the ones place of the answer may be zero. In this case, you should always write a zero in the ones place. The following is an example.
- $3.22÷7$
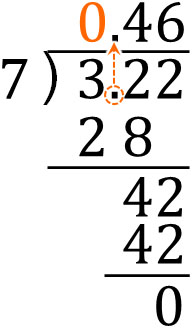
In calculating decimals, the number can be smaller than one. Understand that in the division of decimals, the ones place can be zero.
Division of Decimals Until Divisible
On the other hand, there are some problems that need to be calculated until a number is divisible. In this case, the calculation is done by adding zeros to the right of the decimal.
There are hidden zeros in decimals. For example, 1.4 can be written as 1.400. However, since there is an infinite number of zeros, we omit the zeros in decimals. In any case, it is important to understand that in decimals, there are many zeros to the right of the number.
Therefore, when calculating divisible decimals, add zeros to get the answer. For example, how do we calculate the following?
- $1.4÷25$
When doing this calculation, let’s change the value to 1.40 instead of 1.4. The result is as follows.
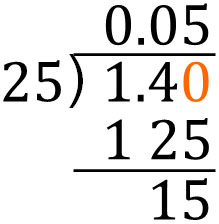
However, the calculation should not end here. From this point, we can do more division. So, let’s change 1.40 to 1.400 and do the next calculation.
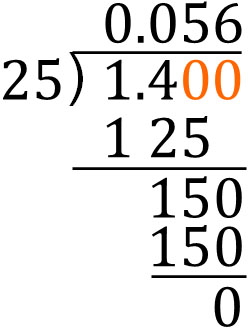
By adding zeros to the right of the decimal, we were able to get the answer. When doing division, if it is divisible, try to get the answer by this method.
When the Divisor Is a Decimal, Move the Decimal Point to Perform the Division
So far, we have discussed division when the divisor is an integer. On the other hand, when a divisor is a decimal number, how do we calculate it?
When the divisor is a decimal, make sure to move the decimal point. By moving the decimal point to the right, you make the divisor an integer. If you don’t do this, you will not be able to divide decimals. For example, how would you do the following calculation?
- $3.22÷1.4$
The long division is as follows.
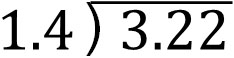
The divisor is 1.4. If we don’t change it to an integer, we will not be able to do the division. So, instead of 1.4, let’s make it 14. Move the decimal point one place to the right.
At the same time, move the decimal point of 3.22 one place to the right as well. Since we have moved the decimal point of the divisor, we need to do the same for the dividend. Therefore, the long division looks like this.
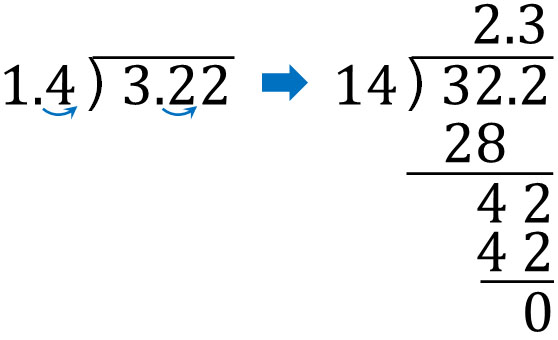
Understand that when the divisor is a decimal, you cannot divide the number unless you change the decimal point. Therefore, we need to move the decimal point like this.
We need to change the divisor to an integer, and how many times we need to move the decimal point to the right depends on the divisor. For example, in the following calculation, we need to shift the decimal point two places to the right.
- $6.848÷2.14$
Let’s do the following long division calculation.
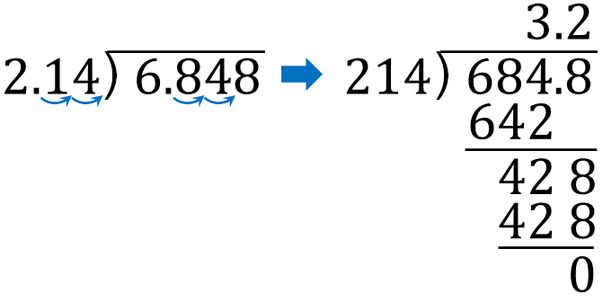
Understand how to move the decimal point and change a divisor to an integer.
Why Moving the Decimal Point Doesn’t Matter
There is a question that is asked by many people. Why is it okay to move the decimal point? The reason for this is that even if you change the position of the decimal point, the answer will be the same.
For example, the following will all give the same answer.
- $100÷20=5$
- $10÷2=5$
- $1÷0.2=5$
- $0.1÷0.02=5$
The answer will be the same if you multiply the number by 10 or 100 for both the divisor and the dividend. For example, compare $10÷2=5$ and $100÷20=5$.

In the same way, we can see that for $1÷0.2$ and $0.1÷0.02$, we can get the same answer by multiplying both the divisor and the dividend by 10 or 100.
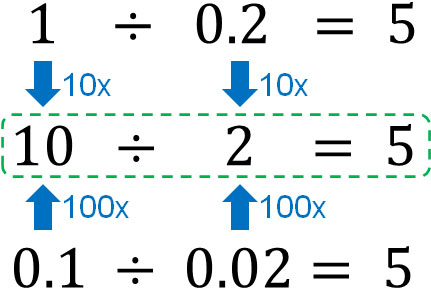
For $1÷0.2$, multiply both numbers by 10 to get $10÷2$. For $0.1÷0.02$, multiply both numbers by 100 to get $10÷2$. In this way, decimals can be converted to integers. This method allows us to divide decimals.
Division of Decimals and Integers with Remainders
So far, we have discussed division when the number is divisible. On the other hand, what should we do with numbers that are not divisible? When an integer is not divisible, we use the remainder. This is also true for decimal division.
For example, how do we calculate the following?
- $22.3÷4$
If you make a long division and calculate it, you will get the following.
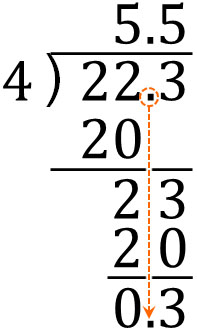
The method of division is the same as the one explained so far. The only difference is that the remainder is given. If you calculate $22.3÷4$, the answer will be 5.5 R 0.3.
When calculating the remainder, make sure to put the decimal point directly below. When calculating decimals, it is easy to make mistakes with the position of the decimal point. If the position of the decimal point is different, the remainder will be different. If this happens, the answer will not be correct, so be sure to check the position of the decimal point.
How to Calculate Division of Two Decimals with Remainder
On the other hand, how do we calculate if the divisor is a decimal? When there is a remainder, it is easy to make a miscalculation if the divisor is a decimal. Therefore, we need to understand how to calculate them.
For example, how do we calculate the following?
- $10.86÷3.3$
In order to do the math, we need to make the divisor an integer. So instead of 3.3, let’s change it to 33. We can do the math as follows.
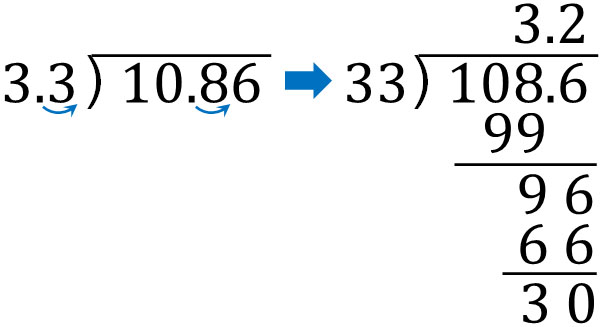
Finally, we need to find the remainder. We must pay attention to the position of the decimal point in the remainder; it must be put directly below the previous decimal point. The result is as follows.
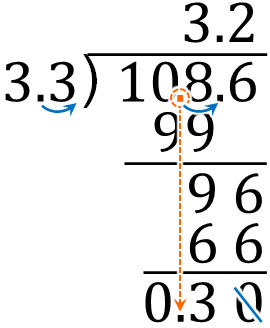
The answer to $10.86÷3.3$ is 3.2 R 0.3.
By multiplying the divisor and dividend by 10, the quotient is 3.2. On the other hand, for the remainder, instead of using 108.6 multiplied by 10 as the reference number, we use the original number, 10.86, as the reference number. We put the decimal point of 10.86 directly below to get the remainder.
Why the Decimal Point Is Different in the Quotient and the Remainder
The reason why it is easy to make miscalculations when dividing decimals is that the position of the decimal point is different for the quotient and remainder. Why does the decimal point change between the quotient and remainder? Let’s understand the reason for this.
As explained before, the quotient is the same even if you multiply the divisor and the dividend by 10 (or 100). The answer is the same, as shown below.
- $100÷20=5$
- $10÷2=5$
Next, let’s try multiplying by 10 for the non-divisible numbers. What will be the answers to the following questions?
- $100÷30=3$ … $10$
- $10÷3=3$ … $1$
As you can see, the quotient is the same even if we multiply the divisor and the dividend by 10. On the other hand, we can see that the remainder is 10 times larger. Also, if we multiply the divisor and the dividend by 100, the remainder is 100 times greater. In division, if we multiply numbers by 10 or 100, the remainder also increases accordingly.
If the remainder is 10 or 100 times larger than the original number, the answer will be different. For example, in the case of $10÷3$, if we multiply the divisor and the dividend by 10, as explained earlier, the remainder will be 10 times larger than the original number.
Even though the divisor is 3, the remainder is 10. Therefore, it is obvious that the answer is wrong.
So when dividing, use the number before multiplying by 10 (or 100) for the remainder. By using the number before the decimal point is moved as the reference, we can add the decimal point in the correct place for the remainder.
Calculating Decimals to Find the Quotient and the Remainder
When we do division, the expression may contain decimals. So, let’s understand how to divide them.
When dividing decimals, it is easy if the number is divisible. All you have to do is to divide in the usual way, paying attention to the position of the decimal point. If the divisor is a decimal, you can change the divisor to an integer by moving the decimal point.
On the other hand, if there is a remainder, it is easy to make a miscalculation. If the divisor is a decimal, the quotient is based on the number after the decimal point is moved. Also, the remainder is based on the number before the decimal point is moved, and then the decimal point needs to be added.
Understand that there are rules for these calculations and perform division calculations involving decimals.