In elementary school arithmetic, we learn multiplication. Multiplication is used frequently in our daily lives. If you can’t do multiplication, you can’t calculate money when shopping. Therefore, it is necessary to be able to do multiplication.
So how can we do multiplication? First of all, you need to understand the meaning of multiplication.
We also need to be able to multiply integers not only by 1-digit numbers but also by 2-digit and 3-digit numbers. In this section, we will explain how to calculate not only one-digit multiplication but also two- and three-digit multiplication.
Table of Contents
The Reason Why We Need to Calculate Multiplication
Why do we need to do multiplication? The reason is that multiplication is a faster way to calculate. For example, what is the answer to the following question?
- There is a car that can carry four people. If there are five cars, how many people can ride in them?
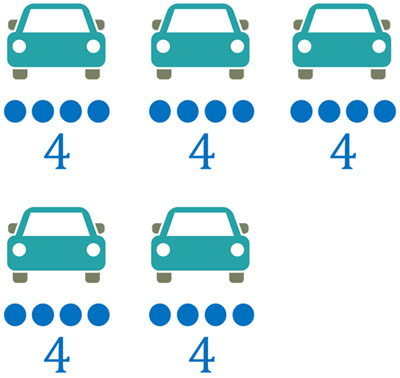
Since four people can fit in one car, we can calculate by addition as follows.
- $4+4+4+4+4=20$
However, this method of calculation is too slow. So, let’s use multiplication. If you use multiplication, you can quickly calculate as follows.
- $4×5=20$
Since there are five cars that can carry four people, we can create the equation $4×5$.
Next, let’s increase the number of cars that can carry four people, one by one. The number of people that can ride in cars is as follows.
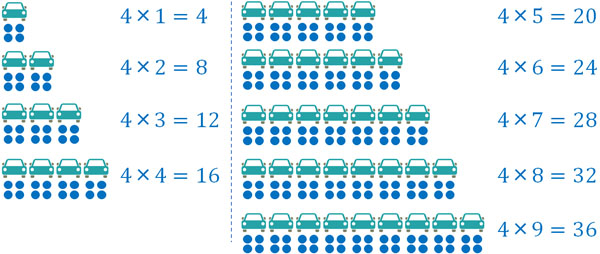
Thus, for each additional car, the number of passengers increases by four. Using multiplication, you can quickly calculate the number of people who can fit in cars.
You Must Memorize Multiplication Table
In order to be able to do the math, you must memorize all the one-digit multiplications. If you don’t remember them, you won’t be able to do math calculations. When multiplying numbers, you can quickly figure out what the answer will be in one-digit multiplication.
You need to memorize the following one-digit multiplication table.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
From this multiplication table, we can calculate as follows.
- $2×7=14$
- $6×3=18$
- $4×9=36$

Of course, it is difficult to memorize all multiplication. Therefore, it is best to start with simple multiplication, such as multiplication tables for two and five.
Also, the multiplication table of 7 and 8 is difficult even for adults, and they often make mistakes in their calculations. So, study and memorize all single-digit multiplications over and over again.
Long Multiplication: One-Digit and Two-Digit Multiplication
After being able to multiply one-digit by one-digit, the next step is learning to multiply one-digit by two-digit. You can multiply one-digit by two-digit by using long multiplication (or column multiplication). For example, how can we do the following calculation?
- $34×6$
When doing this calculation, let’s create the following equation.
$\begin{array}{rr}
& 34\\
×\big{)}&6\\
\hline
\end{array}$
Even for adults, it is difficult to perform one-digit by two-digit calculations by mental arithmetic. Therefore, whenever it is not a one-digit multiplication, you should always create this expression.
The first step is to multiply single-digit numbers. Calculate $4×6$ first.
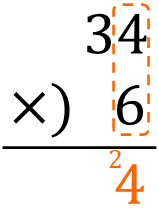
If we calculate it, we get $4×6=24$. Of the 24, 4 is the ones place, so we just write it. On the other hand, 2 is the tens place, so we have to carry it. So, let’s write the number in smaller sizes. This is because the tens place has not been calculated yet.
Next, let’s multiply the tens place. Do $3×6$ and calculate the tens place.
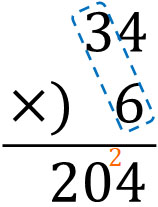
Calculating this, we get $3×6=18$. So write 18 in the tenth place. But when we calculated the ones place, 2 was carried. So, we add 2 to 18. Since $18+2=20$, we must write 20 in the tens place instead of 18.
In this way, we can see that the answer is 204.
Calculating Multiplication with 2-Digit Numbers: 2-Digit by 2-Digit
Next, let’s multiply two digits by two digits, which is a bit more complicated than multiplying one digit by two digits. For example, how do we calculate the following?
- $27×32$
First, let’s create the following equation.
$\begin{array}{rr}
& 27\\
×\big{)}&32\\
\hline
\end{array}$
The first calculation we need to do is the same as before, the calculation of one digit and two digits. It goes as follows.
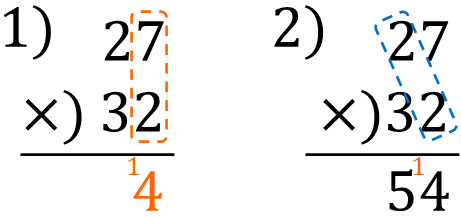
Next, let’s calculate $27×3$. The important thing to remember is that 3 is the tens place. Therefore, when you calculate long multiplication, try to shift one place to the left. It goes as follows.
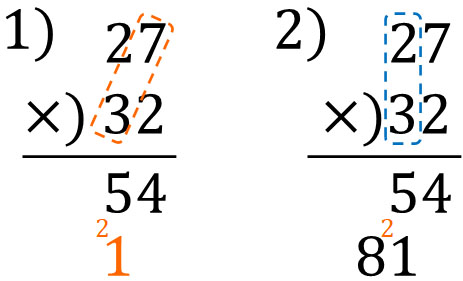
Finally, we add the numbers we calculated. If we add the numbers upper and lower, we get the following.
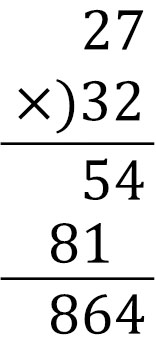
The key point is that when calculating $27×3$, it must be written one place to the left. Even though the calculation is $27×3$, the actual calculation is $27×30$ because 3 is the tens place. Therefore, when you do the calculation, you need to shift it one place to the left.
After that, let’s add up the numbers, paying attention to the upper and lower places.
How to Multiply with 3-Digit Numbers: Two-Digit by Three-Digit
Once you can do two-digit multiplication, you can do three-digit multiplication. The procedure is the same as before. However, since this is a three-digit multiplication, you need to pay attention to the calculation of the carrying. For example, what should we do for the following calculation?
- $463×34$
First, let’s create the following equation.
$\begin{array}{rr}
& 463\\
×\big{)}&34\\
\hline
\end{array}$
As before, let’s first calculate $463×4$.
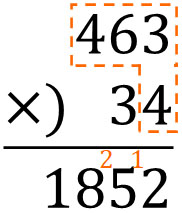
Next, we calculate $463×3$. 3 is the tens place, so we shift it one place to the left.
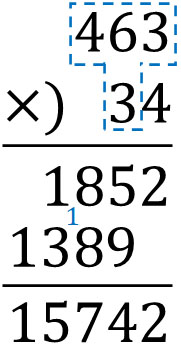
Finally, by adding the upper and lower numbers, the answer is 15742.
How to Calculate Numbers with Multiple Zeros
When multiplying, it is easy to make mistakes with zeroes. When there are multiple zeros, it is easy to make a mistake. For example, how do you calculate the following?
- $260×200$
When calculating by long multiplication, it looks like this.
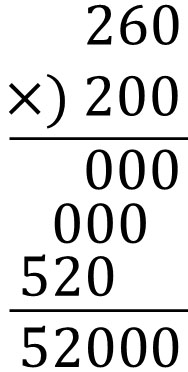
As you can see, the answer is 52000. However, since there are many zeros, it is easy to make a miscalculation. So, let’s do a simpler calculation.
When there are multiple zeros, calculate a number other than zero. In the previous calculation, instead of $260×200$, calculate $26×2$ first. After that, add the three zeros you omitted.
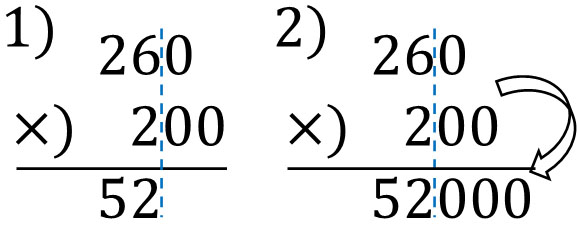
This calculation gives the same answer as before, 52000. When there are zeros, you can avoid mistakes by omitting zeros from the calculation. Then add the omitted zero to get the answer.
Multiplication in Elementary School Math
After learning how to do addition and subtraction, the next step is to learn multiplication. So, let’s make sure you can do multiplication.
Unlike addition and subtraction, multiplication requires you to memorize the multiplication table. If you don’t remember it, you won’t be able to do multiplication. Therefore, you need to study it over and over again so that you can use the multiplication table.
After that, you need to be able to do two- and three-digit multiplication. By using long multiplication, you will be able to calculate even multi-digit multiplication.