In elementary school, we learn decimals in arithmetic. Since multiplication is a common problem in decimals, you need to be able to do multiplication.
Multiplication of decimals is the same as doing long multiplication. You need to pay attention to the position of the decimal point, but there is no major difference except that there is a decimal point.
So how do we multiply decimals? In this section, we will explain how to multiply decimals in elementary school math.
Table of Contents
How to Multiply Decimals by Integers
First, let’s learn how to multiply decimals by integers. How do we multiply decimals by integers? When doing long multiplication (or column multiplication), the numbers should be aligned to the right. For example, suppose you have the following math problem.
- $2.13×41$
When doing multiplication, create the following equation.

After that, do the long multiplication. Let’s ignore the decimal point and do multiplication. After you get the answer, place the decimal point directly below it. The result will look like this.
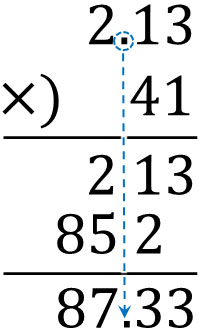
This step allows you to multiply decimals and integers. The only difference between this step and integer multiplication is that you have to put the decimal point directly below after answering.
Why Do We Align Numbers to the Right in Long Multiplication?
In addition and subtraction, we always align the digits. On the other hand, when multiplying decimals, the numbers are aligned to the right. Why is it not necessary to align the digits in multiplication?
As with all multiplication, it is not necessary to align the digits when doing calculations. This is because multiplication is used to indicate how many times a particular number is multiplied. For example, $4.1×2$ means that there are two 4.1s. Therefore, instead of aligning the digits, the numbers are aligned to the right.
On the other hand, what about addition (or subtraction)? For example, when calculating $48-3$, you must always subtract from the ones place; when subtracting 3 from 48, you must subtract 3 from 8, which is the ones place, and not 3 from 4, which is the tens place. In addition and subtraction, the digits have a great deal of meaning.
For this reason, the digits should be aligned in long addition and long subtraction, but aligned to the right in long multiplication.
Multiplication of Decimals by Decimals: Pay Attention to the Position of the Decimal Point
How do we multiply decimals by decimals? Let’s understand how to multiply decimals by decimals, as well as decimals by whole numbers.
The basic idea is the same. When you do multiplication, make sure that the numbers are aligned to the right. For example, how would you do the following calculation?
- $3.24×1.2$
First, let’s make a long multiplication as follows.
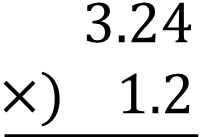
The calculation method is the same as before, ignoring the decimal point and multiplying. The result is as follows.
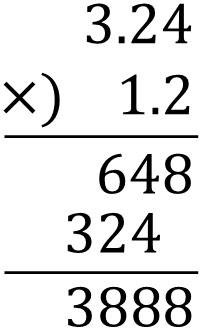
Next, let’s add the decimal point that we ignored to the answer. The way to do this is to count how many times you can move the decimal point to the right. For example, for 3.24, you can move the decimal point two places to the right. Also, for 1.2, you can move the decimal point one place to the right.
Since we can move the decimal point three places to the right in total, we must put the decimal point in the third place from the right in the answer. The result is as follows.

Let’s see how many times you can move the decimal point to the right like this. Then, add the decimal point to your answer.
In the multiplication of decimals by integers, we explained earlier that the decimal point is added directly below the answer after the calculation. In the multiplication of decimals by integers, when you compare the answer to the decimal, the decimal point will be in the same place. On the other hand, when multiplying decimals by decimals, you have to think about where the decimal point is.
-The Reason Why Multiplication of Decimals Increases the Number of Digits
When multiplying decimals by decimals, the number of digits to the right of the decimal point increases. Why does this happen? The reason is that the multiplication of decimals by decimals creates smaller numbers.
For example, if you multiply 0.1 by 0.1, the answer is 0.01.
- $0.1×0.1=0.01$
By multiplying decimals by decimals, we have created a smaller number. In any case, it is important to understand that the multiplication of decimals by decimals produces smaller numbers. This is why the multiplication of decimals by decimals results in more digits to the right of the decimal point.
Calculate Using Approximate Numbers to Avoid Mistakes
When multiplying decimals by decimals, a mistake in the digits can result in a different answer. Is there a way to prevent miscalculation?
In order to avoid mistakes in the position of the decimal point, use approximate numbers. For example, how do you calculate the following?
- $25.3×2.85$
If you do this calculation, the answer will be 72.105. To roughly check if the answer is correct, let’s simplify the multiplication. In other words, make it 25 instead of 25.3 and 3 instead of 2.85. Round off the numbers to the nearest whole number. Then you will get the following.
- $25×3=75$
As you can see, the answers of 72.105 and 75 are similar, so the decimal point is correct. For example, if the answer that comes up is 721.05, you can clearly see that the decimal point is wrong. In this way, you can check beforehand if the answer is correct.
Simplifying Multiplication of Numbers with Multiple Zeros by Decimals
When doing arithmetic calculations, there are cases that you need to calculate numbers with multiple zeros. When multiplying integers by decimals, there is a way to simplify the calculation.
The more you avoid difficult calculations, the less likely you are to make miscalculations, and you can get the correct answer. So, let’s understand how to simplify the equation. In multiplication, you can move the decimal point to the right by a number of zeros. For example, let’s do the following calculation.
- $5000×0.04$
When you do this calculation, you can move the decimal point of 0.04 to the right by two. Then for the number with 0, add the decimal point to the second place from the right. The result is as follows.

For 50.00, there is a rule to omit the zeros to the right of the decimal point. Therefore, it is written as 50 instead of 50.00.
In any case, this makes the calculation much easier. Instead of $5000×0.04$, we can change the expression to $50×4$. Thus, we see that the answer is 200.
Why is it possible to move the decimal point? It is not possible in addition or subtraction, but it is possible in multiplication (or division). As we explained earlier, in multiplication, you don’t need to align the digits. For example, the following multiplications all have the same answer.
- $1×1=1$
- $10×0.1=1$
- $100×0.01=1$
As you can see, the answers are all 1. Also, by moving the decimal point, we can change all of them to a $1×1$ expression. Since there is no need to adjust the digits, let’s simplify the equation by changing the position of the decimal point.
How to Make Percentage Calculations Easier
If you understand this method, you will be able to calculate percentages easily. This is because decimals are almost always used in percentages. For example, 4% is 0.04. Also, 12% is 0.12. So let’s use what we have learned so far in calculating percentages.
For example, what is the answer to the following question?
- How much is 12% of \$4000?
The equation for this question is $4000×0.12$. However, this equation is complicated. So, using the knowledge explained earlier, shift the decimal point as shown below.
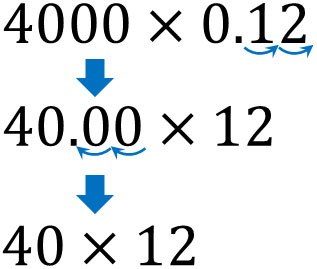
In this way, the equation becomes $40×12$ instead of $4000×0.12$. Therefore, we know that the answer is \$480.
We often calculate percentages in our daily lives. If we move the decimal point in calculations, we will be able to get the answer faster.
Multiplying and Long Multiplication of Decimals
Decimals are numbers that include less than one. Since we often need to multiply decimals, it is important to understand how to do it.
Multiplication of decimals by integers is not difficult. On the other hand, when multiplying decimals by decimals, pay attention to the position of the decimal point. It is good to check how many times you can move the decimal point to the right, and then give the correct answer. If you use a rough number to do the calculation, you can guess if the decimal point is in the correct place or not.
Also, when multiplying numbers with zeros, you can simplify the equation. This is a method that can be used frequently, especially when calculating percentages, so make sure you understand how to do it.