Triangles and quadrilaterals are the most common shapes used in plane figure problems. If you don’t understand the properties of triangles and quadrilaterals, you won’t be able to solve elementary school math problems involving shapes. In particular, angles are important in geometry problems, so learn the angles of triangles and quadrilaterals.
There are different types of triangles and quadrilaterals; depending on the angles, the name of a triangle changes. Similarly, the name of a quadrilateral varies depending on the angles.
Learn the angles and types of triangles and quadrilaterals. If you don’t understand the angles and names of the shapes, you won’t be able to solve the problems, so you need to understand the relationship between them. So, we will explain the angles of triangles and quadrilaterals.
Table of Contents
The Sum of the Interior Angles of a Triangle Is 180°
A shape with three angles is called a triangle. The following are all triangles.

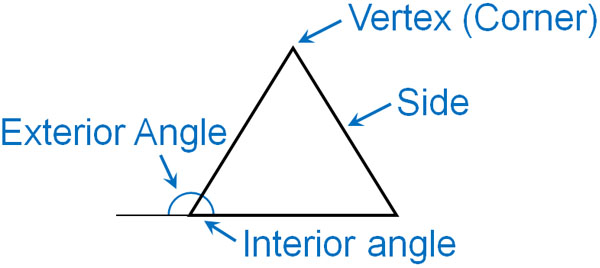
In a triangle, each place is named as follows.
Triangles have the property that if you add up the three interior angles, you get 180°. Using this property, you can calculate an angle you don’t know.
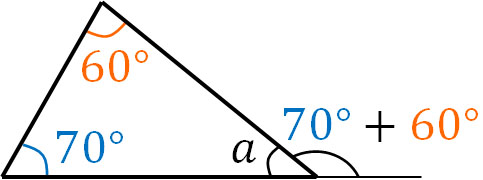
For example, what is the angle of $a$ below?
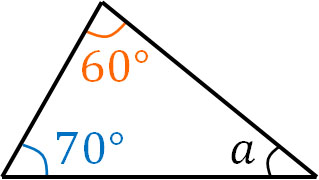
If we add the two interior angles, we get $60+70=130$. Also, if we add all the interior angles of the triangle, we get 180°. Therefore, by subtracting 130° (the sum of two interior angles) from 180°, we can find the angle of $a$.
- $180-130=50$
Thus, we know that the angle of $a$ is 50°.
Why Is the Sum of the Three Angles 180°?
In all triangles, the three interior angles add up to 180°. So, why do the three angles add up to 180°? Let’s think about the reason.
Suppose we have a triangle with angles $a,b,c$ as shown below.
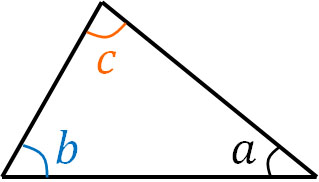
Next, place a triangle of the exact same shape as follows.
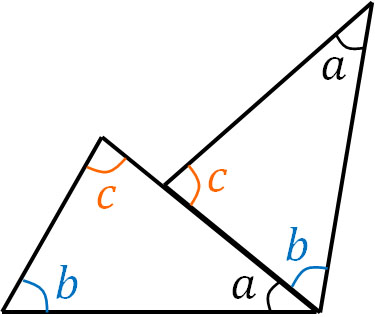
Then the angle $a$ and the angle $b$ will be next to each other. Next, place angle $a$, angle $b$, and angle $c$ next to each other as follows.
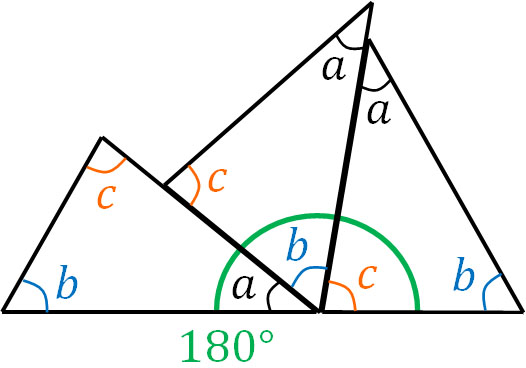
As a result, we find that we can create 180° by arranging angle $a$, angle $b$, and angle $c$. This is the reason why the sum of the interior angles of a triangle is 180°.
The explanation so far does not mean that we have proved that the sum of the interior angles of a triangle is 180°; it is possible to prove that the sum of the three angles is 180° when you study advanced mathematics, such as in middle school mathematics. However, in elementary school math, this is how it should be understood.
-Adding Two Interior Angles Makes an Exterior Angle
The angle outside the triangle is called the exterior angle. The exterior angle of a triangle has the property that it can be calculated by adding two interior angles. It is as follows.
Earlier, we explained that the sum of the interior angles of a triangle is 180°. So, if we check the previous figure, we can see that when we add the two interior angles, we get the exterior angle.
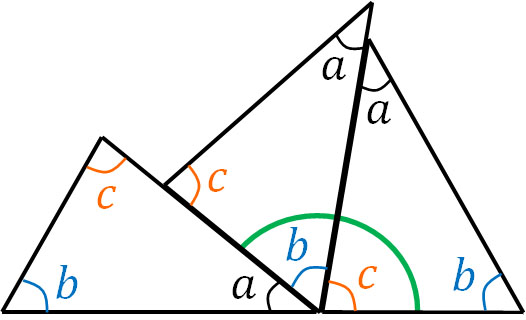
After figuring out the angle of $a$, we can get the exterior angle by subtracting the angle $a$ from 180°. However, we can also calculate the exterior angle by adding the two interior angles.
Types of Triangles: Equilateral Triangle, Isosceles Triangle, Right Angle Triangle
After understanding these properties of triangles, let’s learn about special triangles. Triangles with a specific shape are given a name. So, let’s learn the names of the following triangles.
-Equilateral Triangle
If all three sides have the same length, the triangle is called an equilateral triangle.
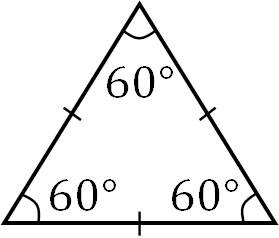
Also, in an equilateral triangle, all angles are equal. The sum of the interior angles of a triangle is 180°, so in an equilateral triangle, all angles are 60°.
- $180÷3=60$
In an equilateral triangle, the angles are fixed.
-Isosceles Triangle
If two sides are equal in length, the triangle is called an isosceles triangle.

In an isosceles triangle, the two angles at the base are always equal.
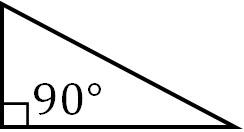
-Right Triangle
A triangle with a right angle (90°) is called a right triangle. The following triangle is a right triangle.
A right-angled triangle with two equal sides is called an isosceles right triangle. The following is an isosceles right triangle.
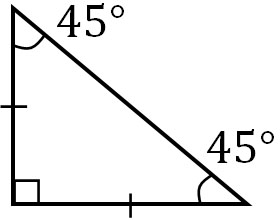
In a right triangle, one of the angles is 90°, so the other two angles add up to 90°.
- $180-90=90$
Also, as mentioned above, in an isosceles triangle, the two angles are equal. Therefore, the other two angles in an isosceles right triangle are 45° each.
- $90÷2=45$
In an isosceles right triangle, we know all the angles.
The Sum of the Interior Angles of a Quadrilateral Is 360°
After learning about the properties of triangles, let’s learn about the properties and types of quadrilaterals. First, how many degrees do the interior angles of a quadrilateral add up to? For all quadrilaterals, the sum of the interior angles is 360°. Make sure you remember this property.
If we add the following four angles (●), the sum will be 360°.

In the case of a quadrilateral, if you know the three angles, you can find the remaining angle; by subtracting the three angles from 360°, you can calculate the remaining one angle.
Draw a Diagonal and Find Out Why the Sum of the Interior Angles Is 360°
So why does the sum of the interior angles of a quadrilateral equal 360°? To understand why, let’s draw a diagonal on the quadrilateral. A diagonal is a line that connects the vertices facing each other, as shown below.
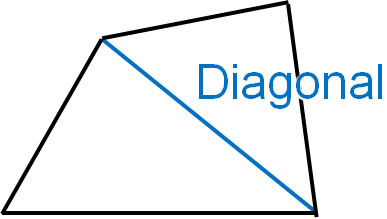
If you draw a diagonal on a quadrilateral, you will get two triangles as shown below.
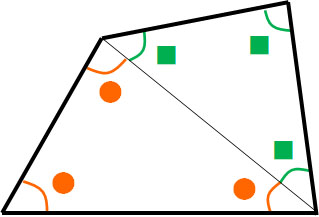
The sum of the interior angles of a triangle is 180°. And since there are two triangles, the sum of the interior angles is 360°. This is because $180×2=360$. So if we add all the interior angles of a quadrilateral, we get a total of 360°.
Important Quadrilaterals Are Squares and Rectangles
What types of shapes are there in a quadrilateral? The most important quadrilaterals are squares and rectangles.
-Square
If all four sides and angles are equal, the quadrilateral is called a square.
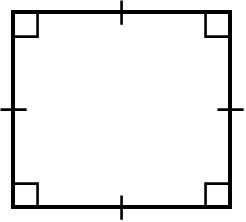
All the interior angles add up to 360°. And since all angles are the same, the angle of the square is 90°.
-Rectangle
If all four angles are 90°, the quadrilateral is called a rectangle.

As in the case of a square, the angle will be 90°. In a rectangle, all the sides do not necessarily have to be the same length.
The Special Shapes of Quadrilaterals Are Parallelogram, Trapezoid, and Rhombus
You will also learn about parallelograms, trapezoids, and rhombuses.
-Parallelogram
If two pairs of opposite sides are parallel, then the quadrilateral is a parallelogram. The following quadrilateral is a parallelogram.
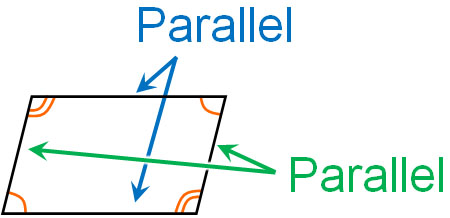
In a parallelogram, the lengths of the paired sides are the same. Also, the sizes of the opposite corners are the same.
-Trapezoid
A quadrilateral with a pair of parallel sides is called a trapezoid.

Each of the four angles is different. Also, the lengths of the four sides are different. The trapezoid is characterized by one set of parallel sides.
-Rhombus
If all four sides have the same length, then the quadrilateral is a rhombus.
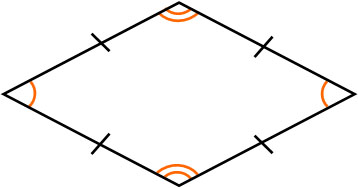
In a square, all four sides are equal in length, and all four angles are equal. A rhombus, on the other hand, is formed when the angles are different but the lengths of the four sides are equal. In addition, in a rhombus, each of the opposite angles is equal in size.
What Happens to the Sum of the Interior Angles of a Polygon?
In addition to triangles and quadrilaterals, how do we think about pentagons and hexagons? Triangles and quadrilaterals are the main shapes you will see in geometry problems. However, you should also understand the properties of pentagons and hexagons.
Regarding the sum of interior angles, the sum of the interior angles increases by 180° as the number of sides increases by one. In other words, it looks like this.
- Triangle: The sum of the interior angles is 180°.
- Quadrilateral: The sum of the interior angles is 360°.
- Pentagon: The sum of the interior angles is 540°.
- Hexagon: The sum of the interior angles is 720°.
Why do we get this result? Let’s draw diagonals in the same way as before.
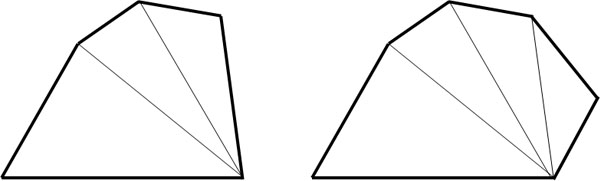
Then, we can make three triangles in a pentagon. Therefore, the sum of the interior angles is 540°.
- $180×3=540$
Also, we can create four triangles in a hexagon. Therefore, the sum of the interior angles is 720°.
- $180×4=720$
So, we have the following.

When calculating the sum of the interior angles of a polygon, check the number of sides. Then, subtract 2 from the number of sides and multiply by 180. As a result, you will get the sum of the interior angles of the polygon. For example, an octagon has eight sides. $8-2=6$. Therefore, the sum of the interior angles of an octagon is 1080°.
- $6×180=1080$
In this way, we can calculate the sum of the interior angles of a polygon.
Learn the Angles and Properties of Triangles and Quadrilaterals
In math, you will be asked questions about shapes. Triangles and quadrilaterals are two of the most common. However, if you don’t understand the properties of triangles and quadrilaterals, you won’t be able to solve them. So first, understand the property of the sum of interior angles of triangles and quadrilaterals.
In a triangle, the sum of the interior angles is always 180°. In a quadrilateral, the sum of the interior angles is always 360°. You can use this property to calculate other angles.
Let’s learn about the special types of triangles and quadrilaterals. Triangles include equilateral triangles, isosceles triangles, and right triangles. Quadrilaterals include squares, rectangles, parallelograms, trapezoids, and rhombuses. You need to remember the properties of all of these shapes.
When solving geometry problems, understand the properties of each shape. Then you will be able to solve angle problems.