When dividing fractions, there is a right way to do it. First of all, you do not do division with fractions. To be more precise, all dividing fractions need to be converted to multiplying fractions. In other words, in order to do the division of fractions, you need to understand how to convert them into the multiplication of fractions.
When converting dividing fractions into multiplying fractions, the reciprocal is always used. By flipping the numerator and denominator, we can change the division to multiplication.
So, what is a reciprocal? And why does the reciprocal make dividing fractions into multiplying fractions?
When doing math calculations, it is important to know why. In this article, we will explain why the reciprocal is a key when dividing fractions.
Table of Contents
What Is the Reciprocal in Fractions?
First of all, what is a reciprocal? Before learning how to divide fractions, all of us are taught reciprocals. A reciprocal is a number with the numerator and denominator turned upside down.
For example, the reciprocal of $\displaystyle\frac{3}{4}$ is $\displaystyle\frac{4}{3}$.
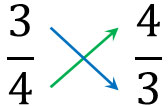
The concept of reciprocals is simple since we only need to swap the numerator and denominator.
By the way, the reciprocal of 3 is $\displaystyle\frac{1}{3}$. 3 is $\displaystyle\frac{3}{1}$. Therefore, the reciprocal of $\displaystyle\frac{3}{1}$ is $\displaystyle\frac{1}{3}$. Integers also have reciprocals.
A Reciprocal Is a Number That Becomes 1 When Multiplied by Another Number
To be more precise, a reciprocal is a number that becomes 1 when multiplied by another number. In other words, if you multiply a number by a number and the answer is 1, that number is reciprocal.
Earlier, we explained that the reciprocal of $\displaystyle\frac{3}{4}$ is $\displaystyle\frac{4}{3}$. The reason for this is that when we multiply $\displaystyle\frac{3}{4}$ by $\displaystyle\frac{4}{3}$, the answer is 1.
- $\displaystyle\frac{3}{4}×\displaystyle\frac{4}{3}=1$
However, when finding the reciprocal, it is difficult to understand the explanation as “the number that becomes 1 after multiplication.” So, let’s remember that the reciprocal is the number whose numerator and denominator are flipped over.
In Dividing Fractions, Use Reciprocals to Convert into Multiplying Fractions
So how do you do the division of fractions? In dividing fractions, we always use reciprocals. To be more precise, when dividing fractions, you need to convert the divisor into the reciprocal and use it as a multiplication expression.
For example, how would you do the following calculation?
- $\displaystyle\frac{2}{3}÷\displaystyle\frac{5}{4}$
In this case, after changing to multiplying fractions, let’s make $\displaystyle\frac{5}{4}$ the reciprocal. The result is as follows.
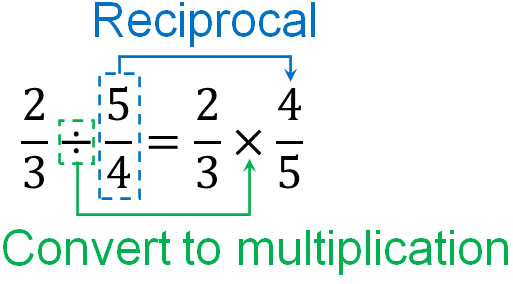
By using reciprocals in this way, all division of fractions can be converted to the multiplication of fractions. No one calculates the division of fractions. Always convert dividing fractions to multiplying fractions. If you do not, there is a high probability that you will make a miscalculation.
After changing the expression by using the reciprocal, the calculation method is the same as for general multiplying fractions. Multiply the numerators by each other and the denominators by each other to get the answer. Also, if you can simplify the fractions, make the number of fractions smaller.
Why Can Dividing Fractions Be Turned into Multiplication with Reciprocals?
Why can we change the division of fractions into multiplication with reciprocals? Many people understand that we use reciprocals when calculating the division of fractions. However, they are unable to explain why. So, let’s understand the reason for this.
There are several ways to explain why it is okay to use reciprocals in dividing fractions. So, we will first explain how to understand it intuitively.
What is the answer to the following question?
- $8÷2$
The answer to this question is 4. So, why is 4 the answer? There are two ways to think about it.
- What is the answer after dividing 8 into two equal parts?
- How many 2’s does 8 contain?
Among these, let’s use the “How many 2’s does 8 contain?”
Next, how many $\displaystyle\frac{1}{2}$ are contained in 2? This question has the same meaning as $2÷\displaystyle\frac{1}{2}$. If you check, 2 contains four $\displaystyle\frac{1}{2}$. Therefore, we know that the answer is 4.
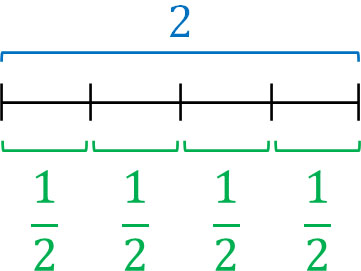
What is important is the fact that all of the equations explained so far can be turned into multiplying fractions by using reciprocals.
- $8÷2=\displaystyle\frac{8}{1}×\displaystyle\frac{1}{2}=4$
- $2÷\displaystyle\frac{1}{2}=\displaystyle\frac{2}{1}×\displaystyle\frac{2}{1}=4$
The figure shows that you can use reciprocals intuitively.
Understand That Multiplication Using Reciprocals Is Valid
So how do we think about the more complicated division of fractions? For example, how do we calculate the following?
- $\displaystyle\frac{1}{2}÷\displaystyle\frac{1}{4}$
All division can be converted to fractions. For example, $1÷3$ would look like this.
- $1÷3=\displaystyle\frac{1}{3}$
This is also valid when calculating division of fractions, such as $\displaystyle\frac{1}{2}÷\displaystyle\frac{1}{4}$. So, let’s create two fractions within a fraction as follows.
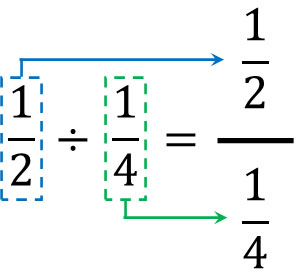
Some people may consider it strange that there are fractions within a fraction. If so, let’s think of fractions as decimals. We can turn each fraction into a decimal as follows.
- $\displaystyle\frac{1}{2}=1÷2=0.5$
- $\displaystyle\frac{1}{4}=1÷4=0.25$
Therefore, we have the following.
- $\displaystyle\frac{1}{2}÷\displaystyle\frac{1}{4}=0.5÷0.25=\displaystyle\frac{0.5}{0.25}$
Thinking in decimals like this, we can see that there is a fraction $\displaystyle\frac{0.5}{0.25}$. Also, $\displaystyle\frac{1}{2}=0.5$ and $\displaystyle\frac{1}{4}=0.25$. Therefore, we have the following.
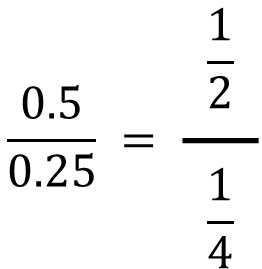
In any case, there are cases like this where there are fractions within a fraction.
Next, for this fraction, let’s use the reciprocal to make the denominator 1. Fractions have the property that if you multiply the numerator and denominator by the same number, the answer will be the same. We have already learned about this property in finding the least common denominator. So let’s multiply the numerator and denominator by the reciprocal of the denominator. The result is as follows.
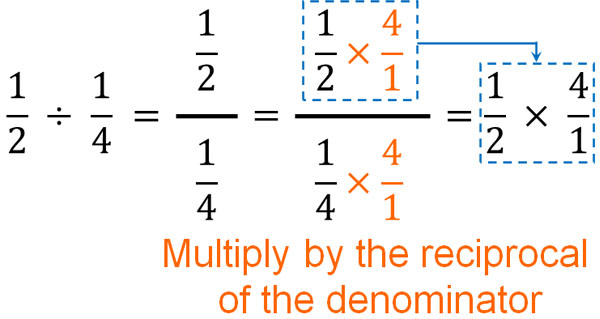
By multiplying by the reciprocal of the denominator, the denominator becomes 1. Usually, the 1 in the denominator is omitted. Therefore, the denominator disappears. Next, let’s look at the numerator. In the numerator, we have an expression that is multiplied by the reciprocal of the denominator.
As you can see, by using the reciprocal, you can change dividing fractions into multiplying fractions. This is the most common way to explain reciprocals to elementary school students.
As mentioned above, we always convert dividing fractions into multiplying fractions. Therefore, it is important to understand why dividing fractions can be converted into multiplying fractions by using reciprocals.
Dividing Fractions Using Reciprocals
In arithmetic, we learn addition, subtraction, multiplication, and division. Among them, the way to divide fractions is different from the normal way. Instead of dividing fractions, we always change it to multiplying fractions.
When changing dividing fractions to multiplying fractions, use the reciprocal. After turning the fraction into the reciprocal, change the division sign to the multiplication sign. As a result, you can change a division equation into a multiplication equation by using reciprocals.
Many people don’t know the reason why you can change division into multiplication by using reciprocals. So, let’s learn the reason. Once you understand the reason, you will be able to calculate with conviction.
We never do the division of fractions. We always convert them into multiplication expressions. Understand this property and calculate the division of fractions.