When calculating fractions, we often do addition and subtraction. When it comes to calculating fractions, addition and subtraction are the most difficult. They are more difficult than multiplication.
The way of doing addition and subtraction of fractions is different from the common way. Also, the calculation method changes depending on whether the denominators are the same or not. If the denominators are different, we need to find the common denominator to make the denominators the same number.
So, how do we add and subtract fractions?
In both adding and subtracting fractions, the denominators must be the same. So let’s take a look at how to add and subtract fractions.
Table of Contents
Addition with the Same Denominator
When adding fractions, do not add both the numerator and denominator. For example, the following calculation is wrong.
- $\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{5}$
Why is this calculation wrong? $\displaystyle\frac{1}{2}$ is the number that halves 1, and $\displaystyle\frac{1}{3}$ is the number that divides 1 into three equal parts.

On the other hand, $\displaystyle\frac{2}{5}$ is the number obtained by dividing 1 into five equal parts and then collecting two of them. Therefore, the calculation $\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{5}$ is smaller than the real answer.
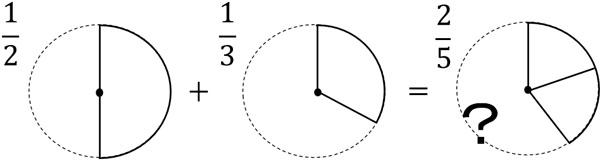
Looking at the figure, we can see that this calculation is obviously wrong.
Why do we make such a mistake? The reason is that we added the denominator. As mentioned above, the denominator is the number that divides 1 into equal parts. Therefore, you must not add the denominators. When the denominators are the same, do not change the denominator.
For fractions with the same denominator, do not change the denominator and just add the numerator. For example, $\displaystyle\frac{3}{4}$ has three $\displaystyle\frac{1}{4}$. Also, $\displaystyle\frac{2}{4}$ has two $\displaystyle\frac{1}{4}$. Therefore, we have the following.
- $\displaystyle\frac{3}{4}+\displaystyle\frac{2}{4}=\displaystyle\frac{5}{4}$
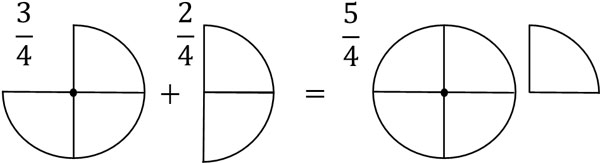
As you can see, the denominator has not changed. In adding fractions, only the number of the numerator changes. The denominator has the property of how many equal parts of 1 are in it. Also, we must not change the nature of the number in addition. Therefore, we do not change the denominator, only the numerator.
Subtraction When Denominators Are the Same
On the other hand, how can we subtract fractions? As before, let’s consider the case where the denominators are the same.
The concept is the same as for addition. The denominator represents the property of the fraction. Therefore, when we do subtraction, the number in the denominator does not change. Instead, you should subtract the number in the numerator. For example, we can calculate as follows.
- $\displaystyle\frac{3}{4}-\displaystyle\frac{2}{4}=\displaystyle\frac{1}{4}$

It is not difficult to understand subtracting fractions if you can do the addition. When subtracting fractions with the same denominator, do not change the denominator; only subtract the numerator.
If the Denominators Are Different, You Cannot Add or Subtract
On the other hand, if the denominators are different, how can we add or subtract? As mentioned above, the denominator represents the property of the fraction. Also, if the numbers have different properties, they cannot be added or subtracted. For example, how do we calculate the following?
- $\displaystyle\frac{3}{4}+\displaystyle\frac{1}{3}$
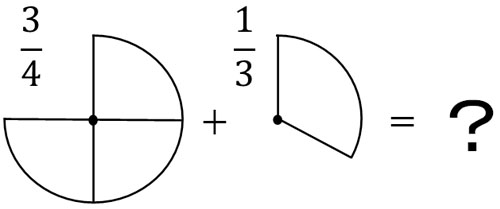
You cannot do addition with these fractions. Since the denominators are different, it is impossible to get a clear answer.
So, let’s make the denominators the same. When the denominators are different, the properties of the numbers are different, so you cannot add or subtract. On the other hand, if the denominators are the same, you can add or subtract. When adding or subtracting fractions, the denominators must be the same.
Making the denominators of fractions the same is called finding the common denominator. So, let’s find the common denominator.
Finding the Common Denominator to Make the Denominators the Same and Performing Addition and Subtraction
To find the common denominator in fractions, use common multiples. For two fractions, check the denominators. For example, how do we calculate the following fractions?
- $\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}$
To do this calculation, let’s find the common denominator. Checking the denominators, the numbers are 2 and 3, and the least common multiple of 2 and 3 is 6. So we find the least common denominator and set the denominators to 6 each as follows.
- $\displaystyle\frac{1}{2}=\displaystyle\frac{1×3}{2×3}=\displaystyle\frac{3}{6}$
- $\displaystyle\frac{1}{3}=\displaystyle\frac{1×2}{3×2}=\displaystyle\frac{2}{6}$
Thus, we can change $\displaystyle\frac{1}{2}$ to $\displaystyle\frac{3}{6}$ and $\displaystyle\frac{1}{3}$ to $\displaystyle\frac{2}{6}$. Since the denominators are the same, we can do the addition. So, let’s add the fractions as follows.
- $\displaystyle\frac{3}{6}+\displaystyle\frac{2}{6}=\displaystyle\frac{5}{6}$
The same method is used for subtraction. For example, in the following calculation, let’s find the common denominator in the same way as before.
- $\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}$
As explained earlier, $\displaystyle\frac{1}{2}$ is $\displaystyle\frac{3}{6}$. Also, $\displaystyle\frac{1}{3}$ is $\displaystyle\frac{2}{6}$. Therefore, we can change the equation to the following.
- $\displaystyle\frac{3}{6}-\displaystyle\frac{2}{6}=\displaystyle\frac{1}{6}$
In both addition and subtraction, the denominators must be the same in order to perform the calculation. Therefore, if the denominators are different, be sure to find the common denominator.
Adding and Subtracting Mixed Fractions: Carrying and Borrowing
So far, we have used proper fractions and improper fractions. The calculation method is the same for mixed fractions. If the denominators are the same, you can add or subtract. For example, how do we calculate the following?
- $1\displaystyle\frac{3}{4}+2\displaystyle\frac{2}{4}$
$1\displaystyle\frac{3}{4}$ means $1+\displaystyle\frac{3}{4}$. And $2\displaystyle\frac{2}{4}$ means $2+\displaystyle\frac{2}{4}$. So, let’s separate the integers and fractions and do the addition. The result is as follows.
- $1\displaystyle\frac{3}{4}+2\displaystyle\frac{2}{4}=3\displaystyle\frac{5}{4}$
Thus, we can calculate the mixed fractions. Note that the number in the numerator of $3\displaystyle\frac{5}{4}$ is larger than the denominator. Therefore, we need to reduce the number in the numerator. $3\displaystyle\frac{5}{4}$ becomes as follows.
- $3\displaystyle\frac{5}{4}=3+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$
It is important to note that $\displaystyle\frac{4}{4}=1$. Therefore, we can change $3\displaystyle\frac{5}{4}$ to $4\displaystyle\frac{1}{4}$. To see this in detail, the calculation is as follows.
$3\displaystyle\frac{5}{4}$
$=3+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$
$=3+1+\displaystyle\frac{1}{4}$
$=4\displaystyle\frac{1}{4}$
Thus, in mixed fractions, you may have to calculate carrying over.
-Subtracting Mixed Fractions
On the other hand, how do we subtract the mixed fractions? As an example, let’s calculate $3\displaystyle\frac{3}{4}-1\displaystyle\frac{2}{4}$. Since the mixed fractions contain integers, let’s separate the integers from the fractions. The result is as follows.
- $3\displaystyle\frac{3}{4}-1\displaystyle\frac{2}{4}=2\displaystyle\frac{1}{4}$
Calculating the integers, we get $3-1=2$. Therefore, the integer part of the mixed fraction is 2. We also have $\displaystyle\frac{3}{4}-\displaystyle\frac{2}{4}=\displaystyle\frac{1}{4}$. Therefore, the fractional part of this mixed fraction is $\displaystyle\frac{1}{4}$.
On the other hand, how do we calculate the following?
- $3\displaystyle\frac{1}{4}-1\displaystyle\frac{2}{4}$
When subtracting fractions, we cannot calculate $\displaystyle\frac{1}{4}-\displaystyle\frac{2}{4}$. So let’s borrow a number from an integer. In mixed fractions, we sometimes have to borrow to calculate. In other words, we change $3\displaystyle\frac{1}{4}$ to the following.
$3\displaystyle\frac{1}{4}$
$=2+1+\displaystyle\frac{1}{4}$
$=2+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$
$=2\displaystyle\frac{5}{4}$
In this case, we can subtract the fractions. It is as follows.
- $3\displaystyle\frac{1}{4}-1\displaystyle\frac{2}{4}=2\displaystyle\frac{5}{4}-1\displaystyle\frac{2}{4}=1\displaystyle\frac{3}{4}$
If you cannot subtract, borrow a whole number to calculate.
Which Answer Is Better, Improper Fractions or Mixed Fractions?
Which is the better answer for fractions, improper fractions or mixed fractions? The answer to this question is clear: you should calculate using improper fractions. If the answer is not specified, you should write improper fractions instead of mixed fractions.
The reason is that mixed fractions are only used in elementary school. In advanced mathematics, such as junior high school, high school, and college mathematics, mixed fractions are never used. In advanced mathematics, you will always use improper fractions.
It is good to learn about mixed fractions as knowledge, but they are rarely used in real life.
Mathematics is used in many fields such as programming, architecture, and space. While we often use improper fractions, we never use mixed fractions. Therefore, try to calculate with improper fractions instead of mixed fractions.
Understand How to Add and Subtract Fractions
Fractions are difficult to calculate until you get used to them. Especially when it comes to addition and subtraction, you have to learn how to do it. In order to do addition and subtraction, the denominators need to be the same.
Also, the denominator does not change when doing addition or subtraction. Only the numerator should be added or subtracted. Therefore, when adding or subtracting, if the denominators are the same, only the number in the numerator will change.
On the other hand, if the denominators are different, you cannot add or subtract. So let’s make the denominators the same. Check the numbers in the denominators to find the common denominator.
There is a correct way to add and subtract fractions. Let’s understand how to add and subtract fractions.