In elementary school mathematics, we learn addition and subtraction. When studying addition and subtraction, a difficult calculation is carrying. Similarly, in subtraction, many elementary school students have difficulty understanding the calculation of borrowing.
When adding or subtracting integers, an important number is 10. By finding the number 10, you will be able to calculate carry and borrow.
In this section, we will explain how to do the addition and subtraction of integers.
Table of Contents
Find the Numbers That Add Up to 10
In mathematics, the following numbers are called integers.
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9…
When adding these numbers, if there is no carry-over, you can calculate them without difficulty. The result is as follows.
- $1+6=7$
- $3+4=7$
- $7+2=9$
So, how do we calculate adding with carrying? For example, the following calculation.
- $3+8$
- $6+6$
In order to calculate addition with carrying, we need to be able to find the number that adds up to 10. What is the number that goes in the following box?
- $2+□=10$
- $6+□=10$
- $5+□=10$
- $1+□=10$
- $9+□=10$
- $8+□=10$
- $7+□=10$
- $3+□=10$
- $4+□=10$
The answer is as follows.
- (1) 8, (2) 4, (3) 5, (4) 9, (5) 1, (6) 2, (7) 3, (8) 7, (9) 6
Try to remember all the answers to each of these. If you don’t know which number to add to make the number 10, you won’t be able to calculate addition with carrying.
Calculating Addition with Carrying
How can we calculate addition with carrying? When doing addition with carrying, we need to make the number 10 by splitting it in two. For example, how do we calculate the following?
- $6+9$
First, let’s figure out what we need to add to the number 6 on the left to get 10. If we add 4 to the number 6, we get 10. So, let’s split the number as follows.
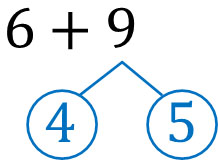
$9=4+5$. In other words, we can split 9 into 4 and 5. After that, add 6 and 4 to get 10.
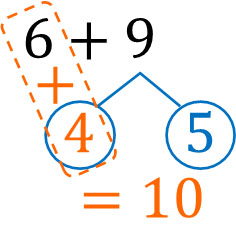
Finally, add the remaining 5. This gives us 15 as the answer. To review, let’s calculate addition with carry as follows.
- Think about what you can add to the number on the left to get 10.
- Split the number on the right.
- Add all the numbers.
If you can’t come up with what to add to the number on the left to make 10, you can’t calculate addition with carrying. Therefore, try to memorize all the numbers that add up to 10.
Adding Two Digits and One Digit
How do we add two-digit numbers by one-digit numbers? The idea is the same as before: find a number that adds up to 10.
For example, let’s do the following calculation.
- $27+5$
Unlike the previous example, it is not possible to make the number 10. Instead, we can add the numbers to get 30. In other words, try to make the round number, such as 10, 20, or 30.
What can we add to 27 to make 30? If we add 3 to 27, we get 30. Let’s split 5 into the following numbers.
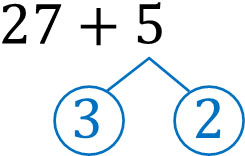
If we add 3 to 27, we get 30. Also, by adding the remaining 2, the answer is 32. The way of thinking is the same as in the previous example. In any case, let’s find a nice round number and do the calculation.
Calculating Subtraction with Borrowing
After learning addition, we need to understand subtraction. In subtraction with borrowing, we need to think about it in the same way as we did with addition. In other words, you need to find the nice round number, such as 10, 20, or 30.
For example, what is the answer to the following question?
- $54-9$
What number should be subtracted from 54 to get the round number? If we subtract 4 from 54, we get 50. So, we can see that we should split 9 as follows.
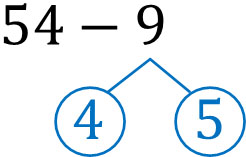
We can split 9 into 4 and 5. After that, let’s calculate as follows.
- Subtract 4 from 54: the number is 50.
- Then subtract 5 from 50: the answer is 45.
This calculation has the same meaning as the following.
- $54-4-5$
When calculating $54-9$, it is easier to calculate if you split the number. Use this method for both addition and subtraction.
Once you get used to it, you will be able to calculate without splitting the numbers. However, until you get used to it, it is good to use this method to do math calculations.
Long Addition in Arithmetic with Two or Three Digits
How do we calculate addition with two or three digits, which is much more complicated than adding one digit?
For example, how do you calculate the following?
- $47+85$
When doing two-digit addition, create the following equation.
$\begin{array}{rr}
& 47\\
+\big{)}&85\\
\hline
\end{array}$
When calculating long addition (or column addition), the first thing we need to do is calculate the ones place. If we add 7 and 5, we get 12, and the ones place in 12 is 2. So, let’s write 2 in the ones place.
The tens place of 12 is 1. So let’s add 1 to the tens place. The result is as follows.
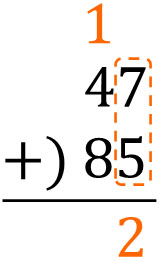
After that, add all tens place. The result is as follows.

Thus, we know that the answer is 132. Here is a review of how to calculate the long addition.
- Add 7 and 5, which are the ones place, and get 12.
- Write 2 of the 12 in the ones place.
- Add 1 of 12 in the tenth place.
- Calculate the tens place.
After calculating the ones place, let’s calculate the tens place.
-Three Digit Addition
What should we do when we want to add three digits instead of two? In this case, the method is the same as before. For example, how should we do the following calculation?
- $285+439$
In the two-digit calculation, we first calculate the ones place. The same is true for the three-digits, calculating the ones place, tens place, and hundreds place in order.
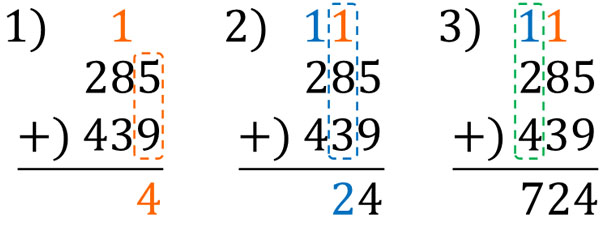
If you can calculate two-digit arithmetic, three-digit addition is not difficult. Let’s learn how to do this so that you can calculate.
Long Subtraction with Two or Three Digits
After learning addition, the next thing we need to learn is subtraction with borrowing. How do we calculate subtraction with two or three digits? As before, let’s solve the problem using long subtraction (or column subtraction).
For example, let’s do the following calculation.
- $53-27$
The equation to create is as follows.
$\begin{array}{rr}
& 53\\
-\big{)}&27\\
\hline
\end{array}$
As with addition, after calculating the ones place, let’s calculate the tens place. The result is as follows.
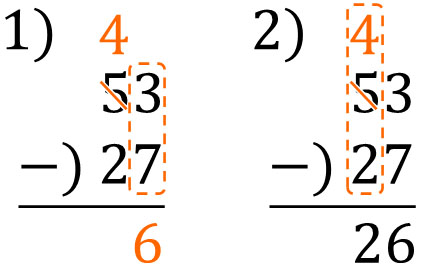
You can’t calculate $3-7$. So, we need to borrow 10 from 53. 10 is borrowed, so $13-7=6$.
The next calculation is in tens place. However, 53 is lending us 10. Therefore, the tenth place is 4 instead of 5. Subtracting 2 from 4 in the tenth place will give you the answer.
In this calculation, 53 is split as follows.
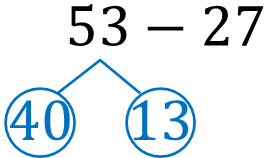
Since $3-7$ is not possible, we made it $13-7$. Also, by splitting 53 into 40 and 13, the tenth place is now 4 instead of 5. In the previous step, we changed the tenth place from 5 to 4. The reason for this is that 40 is created when 53 is split.
-Subtraction by Three Digits
Once you can subtract two digits, you can subtract three digits. For example, how do you subtract the following?
- $616-268$
First, let’s make an equation for long subtraction. It will look like this.

If you are unable to subtract, borrow a number from one larger digit. By borrowing a number, you will be able to subtract it.
Calculating with Carrying and Borrowing
One of the first things we learn in elementary school math is addition and subtraction. However, when doing addition, there are many calculations that require a carry. In addition, there are many cases that you need to do subtraction calculations with borrowing.
So, let’s understand how to do the calculations. When calculating two digits and one digit, it is a good idea to find the round number; 10, 20, or 30 are all round numbers. Using the round number will allow you to calculate including carry or borrow.
In addition, there are cases when we need to calculate integers with two or three digits. It is important to be able to calculate integers with large digits.
There is a method to addition and subtraction. Make sure you understand how to solve problems involving carry and borrow.