In elementary school math, students are asked to solve problems involving circles. A circle is a figure with a round shape. In a circle shape, you are asked to find the length of the circumference and the area of the circle. In order to do these calculations, we need to use Pi. When learning about circles, it is important to understand what pi is.
Circles have different kinds of lengths, and one of them is the radius. Once you know the radius, you can calculate the length of the circumference and the area of the circle.
When calculating the length of a circumference or the area of a circle, you have to use the formula. In other words, if you don’t remember the formula, you can’t solve the problem.
Therefore, we will explain how to think and calculate the length of the circumference and the area of a circle, and what pi is.
Table of Contents
Understanding Important Terms in Circles
There are a number of types of shapes that are round. All of the following have a round shape.

The round shape we learn in elementary school math is a circle. Of the shapes shown in the figure above, the shape on the left is called a circle. Also, when solving circle problems, try to remember the following important terms.
- Circumference: Around the circle.
- Center: The point in the middle of the circle.
- Radius: A line drawn from the center to the circumference.
- Diameter: A line drawn from the circumference to the circumference through the center

These terms are used frequently. Radius and diameter are also terms that are used frequently in our daily lives. So, try to remember what they mean.
What Is Pi: The Number 3.14
In addition to the previous terms, we need to learn about pi when solving circle problems. What is pi? Pi is the value obtained by dividing the circumference by its diameter.
Ancient Egyptian mathematicians already knew that there was a relationship between the circumference and the diameter of a circle. They measured the length of the circumference in the following way.

This time, we used a soft pink string to measure the length of the circumference. Next, we will examine the diameter of the circle. Examine the length of the line passing through the center of the circle, as shown below.

Then, divide the circumference by the diameter of the circle.
- Circumference ÷ Diameter
The value thus obtained is pi. The value of pi is the same for all circles. The pi value is as follows.
- Pi = 3.14159…
Pi is a number that goes on forever. So, in elementary school geometry, we think and calculate “Pi = 3.14.”
When we divide the length of the circumference by the diameter of the circle, the number we happen to get is pi. Also, as mentioned above, all circles have the same value of pi. Pi is a property of the circle.
Using Diameter and Pi to Calculate the Circumference
Once you understand pi, you can calculate the circumference by using the diameter. We explained that by using the length of the circumference and the diameter of the circle, we can calculate pi. This means that we can calculate the circumference by using the diameter and pi.
When calculating the length of the circumference, we use the following formula.
- Circumference = Diameter × 3.14 (Pi)
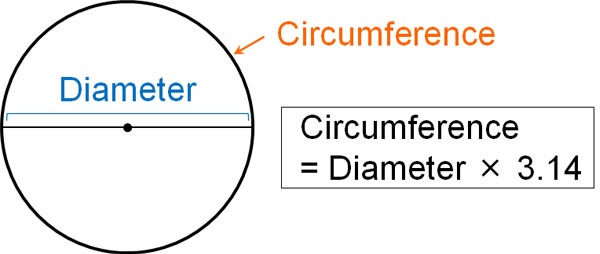
Thus, by multiplying the diameter by pi, we can find the circumference.
Note that if you double the radius, you get the diameter. Therefore, if you know the radius, you can calculate the circumference. After doubling the radius, multiply it by 3.14 (pi) to get the circumference.
- Circumference = Radius × 2 × 3.14 (Pi)
In any case, understand that if you know the diameter or radius, you can calculate the length of the circumference.
Calculating the Diameter from the Circumference
The fact that we can calculate the circumference using the diameter and pi also means that we can use the circumference to calculate the diameter. Multiplication has the same meaning as division. For example, $□×2=6$ can be changed as follows.
- $□=6÷2$.
In the same way, let’s change the formula for calculating the circumference. If the diameter is $□$, the formula is as follows.
- Circumference = $□$ × 3.14 (Pi)
If we change this formula, we get the following.
- $□$ = Circumference ÷ 3.14 (Pi)
In other words, if you remember the formula to find the length of the circumference, you can calculate the diameter from the circumference. Also, if you halve the diameter, you get the radius, so you can also calculate the radius from the circumference.
A formula with an equal sign has the property that both sides can be multiplied or divided using the same number. So, for the formula for circumference, let’s divide both sides by 3.14. In this way, we can change the formula for circumference to the formula for a diameter.
Using Radius and Pi to Calculate the Area of a Circle
There is another important formula that uses pi. It is the formula for finding the area of a circle. Using pi, we can calculate the area of a circle.
The formula for calculating the area of a circle is as follows.
- Area of a circle = Radius × Radius × 3.14 (Pi)
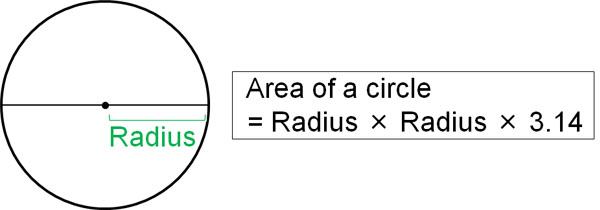
By using radius and pi, we can calculate the area of a circle. Be sure to memorize the formula for calculating the area of a circle.
Calculating the Radius of a Circle from Its Area
The fact that we can calculate the area of a circle by using its radius means that we can calculate the radius by using its area. If the radius is $□$, the area of a circle can be calculated by the following formula.
- Area of a circle = $□$ × $□$ × 3.14
Then, let’s change this formula as follows.
- $□$ × $□$ = Area of the circle ÷ 3.14
For example, if the area of a circle is 50.24 cm2, what is the radius? $50.24÷3.14=16$. Also, when multiplying two equal numbers, find the value that makes 16. Then we know that 4 is the answer. So, if the area of the circle is 50.24 cm2, the radius is 4 cm.
Why Can We Calculate the Area of a Circle Using Radius and Pi?
Why is it possible to calculate the area of a circle using radius and pi? To understand the reason, let’s divide the circle into smaller pieces as follows.
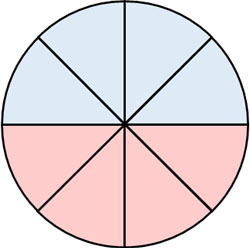
After that, let’s arrange the parts of the circle as follows.

As a result, we can create a parallelogram, as shown below.
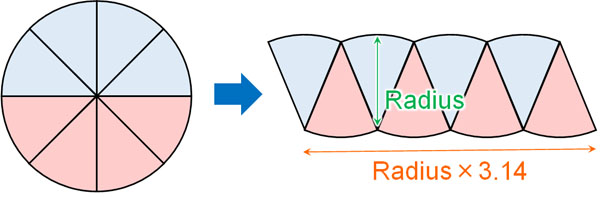
Strictly speaking, it is not a parallelogram because it is uneven. However, if you divide the circle into very small pieces, the unevenness almost disappears and becomes negligible, allowing you to create a parallelogram. Also, if you use the integrals that you learn in high school mathematics, you can use this concept to find the area of a circle.
So, the vertical length of a parallelogram is the radius. On the other hand, the side length is “radius x 3.14.” Checking the figure, the circumference of the orange circle (semicircle) is as follows.
- Circumference of a semicircle = Diameter × 3.14 ÷ 2
Multiply the radius by 2 to get the diameter. Therefore, the circumference of a semicircle is “radius × 3.14.”
- Circumference of a semicircle = Radius × 2 × 3.14 ÷ 2 = Radius × 3.14
Also, if you check the previous figure, you will see that the circumference of the orange circle (semicircle) is the side length of the parallelogram. So, multiplying the vertical (radius) by the horizontal (radius × 3.14) of the parallelogram, we can get the area. The result is the same as the formula for finding the area of a circle.
In this way, we can get the formula for finding the area of a circle. If you want to understand the reason in more detail, let’s try to prove it after learning the integral.
Calculating Circumference and Area of a Circle
Geometry problems involving circles are common. By using the pi ratio, we can calculate the length of the circumference and the area of a circle.
In order to calculate the circumference, you need to know the formula for calculating the circumference. And if you understand the formula, you can use the circumference to calculate the diameter and radius.
In addition to that, you need to learn the formula to calculate the area of a circle. By using the radius and pi, you can calculate the area of a circle. Also, learn the reason why the formula for calculating the area of a circle is valid.
Formulas for the circumference and area of a circle are used frequently. Also, there are many calculation problems related to circles. So, let’s learn the two formulas and be able to use them.