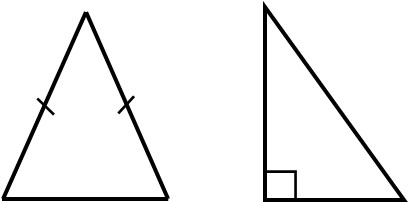
In mathematics, there are two types of shapes that we learn about: isosceles triangles and right triangles. The isosceles triangle and the right triangle are special triangles.
Since they are special triangles, they have their own characteristics. By learning what characteristics they have, we will be able to calculate angles and prove shapes.
Isosceles triangles and right triangles must be studied together. This is because these figures are often given as mixed problems. In other words, by understanding the properties of both isosceles and right triangles, we will be able to finally solve problems.
Therefore, after explaining the properties of isosceles triangles and right triangles, we will explain the theorems for proving that they are congruent.
Table of Contents
Isosceles and Right Triangles Are Special Triangles
Of all the shapes, the most frequently asked geometry problem is the triangle. However, there are different types of triangles. If a triangle satisfies certain conditions, it is called by another name.
Such triangles include the following.
- Isosceles triangle
- Right-angled triangles
Another typical example of a special triangle is the equilateral triangle. A triangle whose side lengths and angles are all the same is an equilateral triangle. As for equilateral triangles, they have simple properties.
On the other hand, isosceles and right triangles have more properties to remember than equilateral triangles. Also, isosceles triangles and right triangles are often given as mixed problems, and it is often impossible to solve them unless you understand the properties of both.
In addition, right triangles have a congruence condition that is available only for right triangles. You must remember this congruence theorem.
Definition, Properties, and Theorems of Isosceles Triangles
It is important to understand the definition of special shapes. In the case of isosceles triangles, what is the definition? Any triangle that satisfies the following conditions is an isosceles triangle.
- Triangles with two equal sides
Whenever two sides are equal, it is an isosceles triangle. Conversely, if all sides are not equal in length, it is not an isosceles triangle. Since it is a definition, the following isosceles triangle will always have AB=AC.
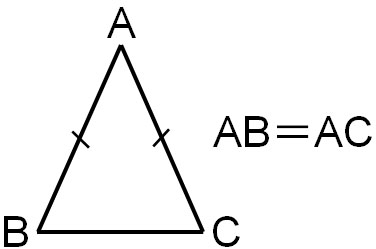
If you are given an isosceles triangle in a math problem, the two sides have the same length.
Also, isosceles triangles have a property (theorem) derived from their definition. One of these theorems is that the base angles are equal. In an isosceles triangle, the two sides are equal, and the two angles at the base are also equal.
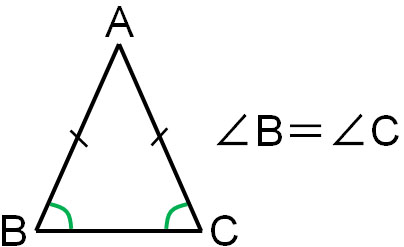
Properties derived from definitions are called theorems. One of the theorems of an isosceles triangle is that the base angles are equal.
Proof That Base Angles of Isosceles Triangles Are Equal
Why are the base angles of an isosceles triangle equal? In mathematics, we study proofs, so let’s prove why the base angles are equal. Consider the following isosceles triangle where point D is the midpoint of BC.
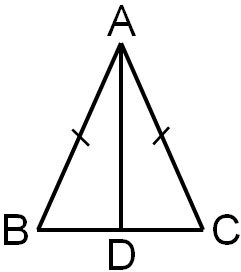
The proof is as follows.
- In △ABD and △ACD
- AB=AC: Definition of an isosceles triangle – (1)
- BD = CD: Point D is the midpoint of BC – (2)
- AD = AD: Common line – (3)
- From (1), (2), and (3), since Side – Side – Side (SSS), △ABD≅△ACD
- Since △ABD≅△ACD, ∠B=∠C
By proving that the triangles are congruent, we can prove that the base angles of an isosceles triangle are equal. In an isosceles triangle, the two sides are equal and the base angles are always equal.
Properties of Right Triangles and Hypotenuse
Another special triangle that we need to learn at the same time as the properties of isosceles triangles is the right triangle. If a triangle has an angle of 90°, it is called a right triangle.
Right triangles have hypotenuse. General triangles do not have a hypotenuse. However, right triangles are special triangles, and we will use the hypotenuse to explain the properties of right triangles. The hypotenuse of a right triangle refers to the following part.

A triangle with an angle of 90° is the definition of a right triangle. Right triangles also have two acute angles in addition to the hypotenuse; any angle smaller than 90° is called an acute angle. In a right triangle, two angles that are not 90° are always acute angles.
Congruence Theorem for Right Angle Triangles: HL
It is important to note that right triangles have their own congruence conditions in addition to the triangle congruence theorems. The four congruence theorems for triangles are as follows.
- Side – Side – Side (SSS) Congruence Postulate
- Side – Angle – Side (SAS) Congruence Postulate
- Angle – Side – Angle (ASA) Congruence Postulate
- Angle – Angle – Side (AAS) Congruence Postulate
In addition to these, there is a congruence theorem that exists only for right triangles. The following is a right triangle congruence theorem.
- Hypotenuse – Leg (HL); Sides other than the hypotenuse are called legs.
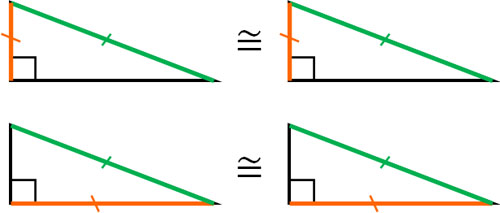
There are a total of five congruence theorems for triangles. In addition to the triangle congruence theorems, try to remember the right triangle congruence condition.
-It’s Not Enough That Two Angles Are Equal
Some people consider the congruence condition of right triangles when the two angles are equal. In this case, however, the two right triangles are not necessarily congruent. There are cases where they have different shapes, as shown below.
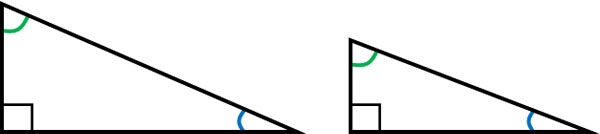
Just because the angles are equal does not mean that they are congruent. Triangles are not congruent if they do not satisfy the congruence condition.
Exercises: Proof of Shapes
Q1: Prove the following figure.
For the following figure, △ABC is an isosceles triangle with AB = AC. If BD⊥AC and CE⊥AB, prove that △BCE≅△CBD.
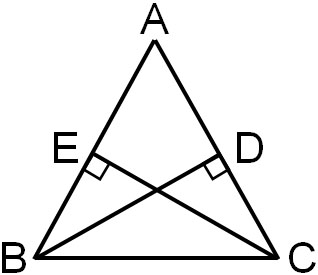
A1: Answer.
Mixed problems of isosceles triangles and right triangles are frequently asked. So, try to understand the properties of the two shapes.
- In △BCE and △CBD
- ∠BEC = ∠CDB = 90°: Given – (1)
- BC = CB: Common line – (2)
- ∠EBC = ∠DCB: Base angles of an isosceles triangle are equal – (3)
- From (1), (2), and (3), since Angle – Angle – Side (AAS), △BCE≅△CBD
Q2: Prove the following figure.
For the figure below, △ABC is a right triangle with ∠ABC = 90°. From point B, draw a line BD perpendicular to side AC. Also, draw a bisector of ∠BAC, and let the intersection points be E and F, respectively, as shown below. Prove that BE=BF.
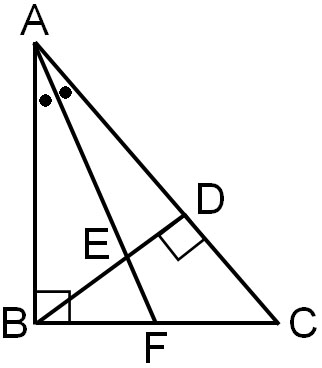
A2: Answer.
There are several possible ways to prove that the lengths of the sides are the same. The most common way is to find congruent triangles. However, looking at the figure, it seems that there are no two triangles that are congruent.
So, let’s think of another way to prove that the side lengths are the same. The property of an isosceles triangle is that the two sides are equal, and the base angles are equal. Therefore, if we can prove that the two angles are the same, then we know that the triangle is an isosceles triangle and the two side lengths are equal.
First, let’s focus on △ABF. ABF is a right triangle, and ∠AFB is as follows.
- $∠AFB=180°-90°-∠BAF$
- $∠AFB=90°-∠BAF$ – (1)
On the other hand, what about ∠AED? △AED is a right triangle, and the angle AED is as follows.
- $∠AED=180°-90°-∠EAD$
- $∠AED=90°-∠EAD$ – (2)
Also, since the vertical angles are equal, ∠AED = ∠BEF. Therefore, for (2), we can replace ∠AED with ∠BEF to get the following.
- $∠BEF=90°-∠EAD$ – (3)
Since ∠BAC is bisected, the angles of ∠EAD and ∠BAF are the same. Therefore, we have the following.
- $∠AFB=90°-∠BAF$ – (1)
- $∠AFB=90°-∠EAD$ – Substitute (3)
- $∠AFB=90°-(90°-∠BEF)$
- $∠AFB=∠BEF$
Thus, we know that △BEF is an isosceles triangle because the angles of ∠AFB and ∠BEF are equal. Also, since it is an isosceles triangle, BE=BF.
Use the Properties of Special Triangles and Prove Them
Problems involving the calculation of angles and the proof of figures are frequently asked in mathematics. In these problems, special triangles are often used. Special triangles include isosceles triangles and right triangles.
There are two characteristics of isosceles triangles. The first is that the two sides are equal. The second is that each base angle is equal. On the other hand, right triangles have a congruence theorem. There is a congruence theorem available only for right triangles, so try to remember it.
It is important to remember that isosceles triangles and right triangles are sometimes asked as mixed problems. You often need to understand the properties of both isosceles triangles and right triangles to be able to solve the problem. Try to answer using the characteristics of both isosceles and right triangles.
As special triangles, isosceles triangles and right triangles are frequently asked. They are important figures in mathematics, so remember their definitions, properties, and congruence theorems before solving them.





