In mathematics, we learn about space figures. We learn the area and volume of a three-dimensional figure, not a plane. One such field is the surface area of prisms and cylinders.
How can we calculate the surface area of prisms and cylinders? When calculating the surface area of a prism or cylinder, the method of calculating surface area varies depending on the shape. However, the basic idea is the same. In fact, there is only one formula for calculating surface area.
But even if the idea is the same, a prism and a cylinder have to be calculated in different ways.
How can we calculate the surface area of prisms and cylinders? We will explain how to calculate the surface area, which is important in space figures.
Table of Contents
Two Types of Pillar Shapes: Prismatic and Cylindrical
There are two main types of pillar shapes: prisms and cylinders. To understand how to find the surface area, we must understand the types of prisms and cylinders.
In the prism, there are various three-dimensional shapes. If it has a triangular shape, it is a triangular prism. If it is a rectangular shape, it is called a quadrangular prism. On the other hand, if it is a round pillar, it is called a cylinder. Each has the following shapes.
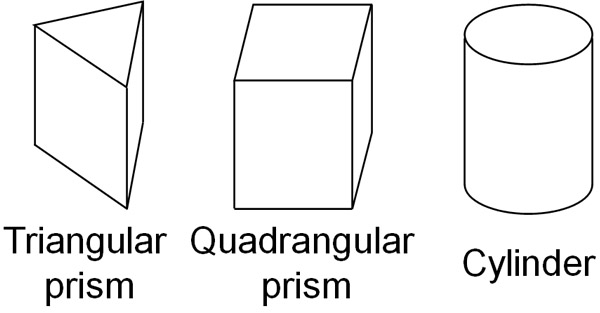
Of course, there are also pentagonal and hexagonal prisms. However, in mathematics, triangular prisms and quadrangular prisms are mainly used as calculation problems.
In any case, when we find the surface area, it is important to understand that there are two types of pillar shapes: prisms and cylinders.
Adding Base Areas and Side Area Yields the Surface Area
How do we get the surface area of prisms and cylinders? The way to do this is to calculate the base areas and side areas. To find the surface area of a prism or a cylinder, calculate the top and bottom base areas and side area, respectively, and add the numbers.
Therefore, the formula for the surface area of a prism and a cylinder is as follows.
- Surface are = Base area × 2 + Side area
Even though it is a formula, it does not mean that you can find the surface area with only one formula. Each part needs to be calculated separately.
For a prism and a cylinder, the base and sides are as follows.
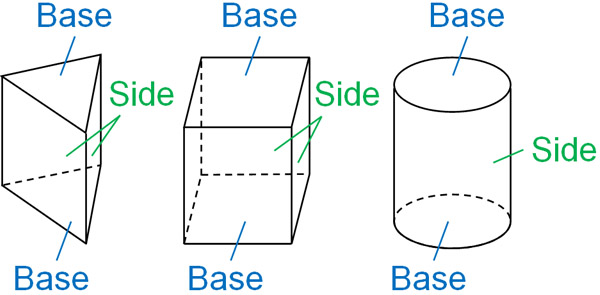
Each of the top and bottom surfaces is a base. This area is the base area, respectively. On the other hand, the side surface is the side. By adding up the sides, we can get the side area. We can then calculate the surface area of the column by adding the two base areas and the side areas.
The Total Area of the Net Is the Surface Area
How do we figure out the area of bases and sides? To do this, we can use nets. After disassembling a three-dimension by using scissors, the figure is expanded to become a flat surface, which is called a net. We can convert a three-dimensional figure into a two-dimensional figure.
For example, the following is a net of a quadrangular prism.
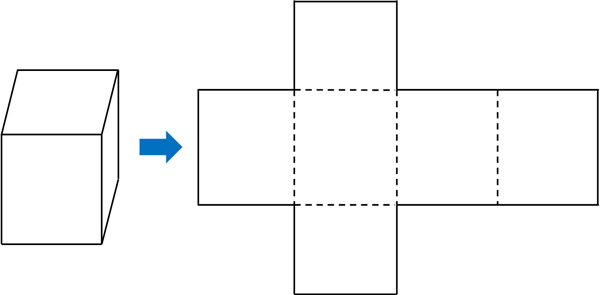
In the calculation of space figures, we will be presented with 3D figures. So use the net to imagine what it would look like if it were converted to a plane and calculate the surface area.
However, the calculation of surface area is different for prisms and cylinders. We will explain each of the two patterns in the following sections.
How to Calculate the Surface Area of a Prism
What are the characteristics of a prism net? As an example, let’s consider the net of a triangular prism. The following is the net of a triangular prism when it is converted to a plane.
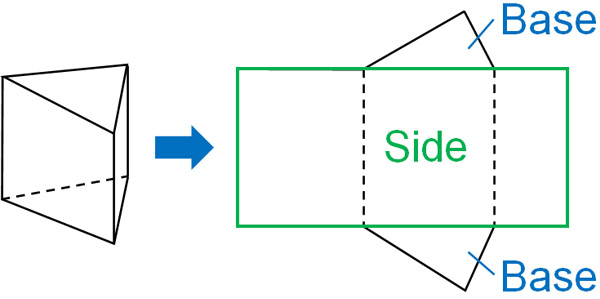
In the nets of the prism, the sides will always be a rectangle (or a square). The side length of the rectangle is equal to the perimeter of the base (orange line). Since both triangular and quadrangular prisms have rectangular sides, the side length of the rectangle can be calculated by adding the perimeter of the base.
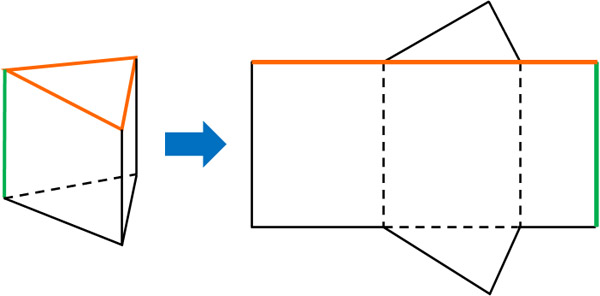
Also, the height of the triangular prism is the same as the vertical length of the rectangle. Therefore, the area of a side can be calculated by the following formula.
- Area of the sides = Perimeter of the base × Prism height
Next, get the base area. The shape of the base depends on what kind of prism it is. If it is a triangular prism, the base is a triangle. If it is a quadrangular prism, the base is a rectangle. So, calculate the base area of each.
Calculating Surface Area from a Cylinder Net
In contrast, how can we calculate the surface area of a cylinder? Let’s consider the net of a cylinder in the same way as for a prism. The net of a cylinder looks like the following.

The height of the cylinder is the same as the vertical length of the rectangle in the net. In short, the concept of the vertical length of a rectangle is the same as that of a prism.
On the other hand, what about the horizontal length of the rectangle? In the case of a cylinder, the horizontal length of the rectangle is the same as the circumference of the base. Therefore, by calculating the length of the circumference, we can find the horizontal length of the rectangle.
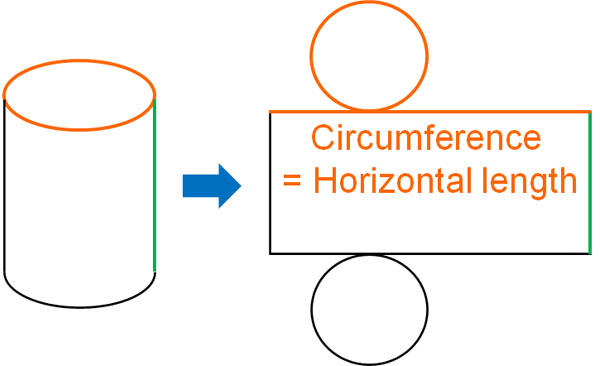
Then, let’s get the base area (area of the circle). The area of a circle can be calculated by using the formula.
In mathematics, we consider the pi as $π$. On the other hand, we can also calculate the pi as 3.14. Either calculation method is correct. However, calculating 3.14 is complicated, so using $π$ as pi is less likely to result in miscalculation.
Exercises: Surface Area of Prisms and Donuts Shapes (Hollow Cylinders)
Q1. Calculate the surface area of the following cylinder. Let the pi be $π$.
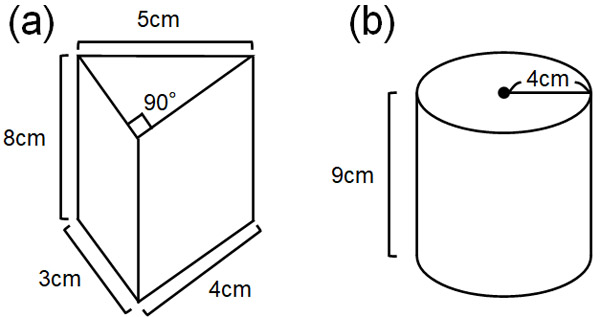
A1: Answers.
(a)
First, let’s calculate the side area. The length of the triangular prism’s surround is $3+4+5=12$ cm. And the vertical length is 8 cm. Therefore, the side area is as follows.
- $12×8=96$
Then calculate the base area. The triangle at the bottom is a right-angled triangle. Therefore, we know that it is a triangle with a width of 4 cm and a height of 3 cm. Substituting the numbers to the formula that yields the area of the triangle, the base area is as follows.
- $4×3×\displaystyle\frac{1}{2}=6$
Finally, add the areas of each. As a reminder, there are two base areas, so we must double them.
- $96+6×2=108$
Therefore, the surface area is 108 cm2.
(b)
First, let’s calculate the side area. The side length of a rectangle is the same as the circumference of base. So, let’s use the formula to find the length of the circumference. The length of the circumference can be found by multiplying the diameter of the circle (8 cm) by the pi ($π$). In other words, the length of the circumference is $8π$.
Also, the vertical length of the sides is 9 cm. Therefore, the side area is as follows.
- $8π×9=72π$
Next, let’s find the base area. Substituting the formula for finding the area of a circle, we get the following calculation.
- $4×4×π=16π$
Finally, add the side area and the top and bottom base areas. The result is as follows.
- $72π+16π×2=108π$
Therefore, the surface area of the cylinder is $108π$ cm2.
Q2: Calculate the surface area of the following cylinder. Let the pi be $π$.
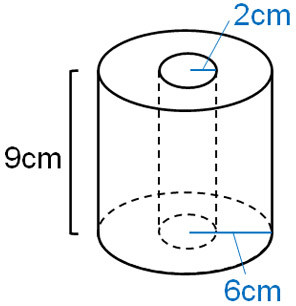
A2: Answer.
One of the advanced problems in calculating the surface area is the donut-shaped cylinder. In addition to calculating the outer area of the cylinder, we must also consider the surface area of the hollow space.
For a donut-shaped cylinder, we calculate three areas. First, let’s find the outer side area of the cylinder. The outer side area can be calculated by the method we have described so far. The diameter of the larger circle is 12 cm. The length of the circumference is $12π$, so the side area is as follows.
- $12π×9=108π$
In the same way, let’s find the inner side area. When considering the net, the horizontal length of the rectangle is equal to the circumference. We can therefore calculate the smaller circumference to get the inner side area.
Even though it is actually hollow, if we assume that there is a cylinder in the hollow, we can make a cylinder net as follows.
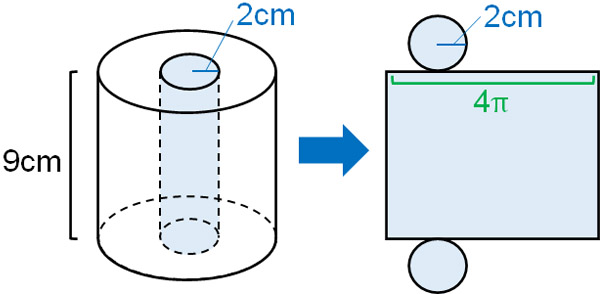
So, let’s calculate the side area of this cylinder. It is as follows.
- $4π×9=36π$
Next, calculate the top and bottom base areas. As a reminder, the base has a hollow surface, as shown below.
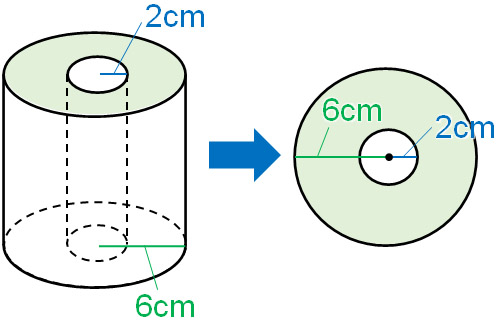
So, let’s subtract a smaller circle from a larger circle. Substituting the numbers to the formula for the area of the circle, the larger circle is $6×6×π=36π$. And the area of the smaller circle is $2×2×π=4π$. Therefore, the base area is as follows.
- $36π-4π=32π$
Finally, add the top and bottom base areas and side areas.
- $108π+36π+32π×2=208π$
Therefore, the surface area of the donut-shaped cylinder is $208π$ cm2.
Calculating the Surface Area of Prisms and Cylinders
When learning space figures, we learn the surface area of prisms and cylinders. The formula for calculating the surface area of prisms and cylinders is to calculate the base and surface area separately, then add them together to get the area. So, when figuring out the surface area of prisms and cylinders, let’s calculate the area of each.
When finding the side area of a prism, the length of the side is the same as the surrounding length of the prism. Then add the top and bottom base areas. For a cylinder, the length of the circumference is equal to the side length of the rectangle. Use this method to calculate the surface area of a prism or cylinder.
These are the ways to calculate the surface area of prisms and cylinders. In mathematics, we may be asked to calculate the surface area of prisms and cylinders. So, let’s understand how to calculate the surface area of prisms and cylinders.