We will learn about similarities in mathematics. One of the important things in the field of similarity is the midpoint theorem (or midpoint connector theorem). By using the midpoints of a triangle, we can calculate the side lengths.
In addition to triangles, we can also calculate the side lengths of trapezoids and prove parallelograms. The midpoint theorem is a concept that can be applied to trapezoids, parallelograms, and other shapes.
If you can calculate the side lengths by understanding the midpoint theorem, you will be able to calculate other cases as well. Even if it is not a case of connecting the midpoints, you will be able to get the side length by using the property of similarity.
In this section, we will explain the midpoint connector theorem, which is important in similarity, and explain the converse of the midpoint theorem, its proof, and how to solve advanced problems.
Table of Contents
- 1 What Is the Midpoint Theorem for Parallel Lines?
- 2 The Side Lengths Can Be Calculated from the Similarity Ratio Without Using the Midpoint
- 3 Using the Midpoint Theorem in Quadrilaterals Creates Parallelograms
- 4 Exercises: Midpoint Theorem and Similarity of Triangles
- 5 Calculating Lengths Using Parallel Lines
What Is the Midpoint Theorem for Parallel Lines?
When we see the term midpoint theorem, it may sound difficult. However, after learning about triangle similarity, the midpoint theorem is very easy to understand.
First of all, we consider triangles in the midpoint theorem. Consider a triangle with two midpoints. In that case, the figure will look like the following.
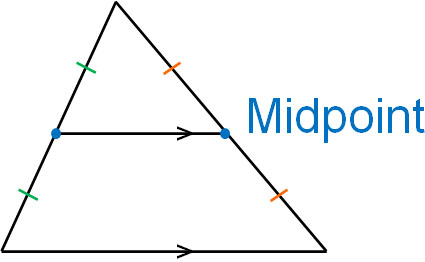
In this case, the following two things are true.
- The base and the line connecting the midpoints are parallel.
- The base length is twice the length of the line connecting the midpoints.
This is the midpoint theorem. The midpoint theorem can be understood as a triangle with a similarity ratio of 1:2. By connecting the midpoints of a triangle, we can create a similar triangle, and the similarity ratio is 1:2.
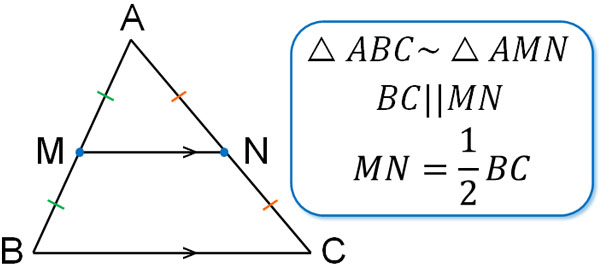
Since they are the midpoints of the sides, it is easy to understand that the similarity ratio is 1:2. This property is the midpoint theorem.
Explaining Why Midpoint Theorem Is True in Proof
So, why does the midpoint theorem hold? Let’s try to prove the reason. Since they are midpoints, we know that the side ratio will always be 1:2. Therefore, we can prove the following.
- In △ABC and △AMN
- ∠BAC = ∠MAN: Common angle – (1)
- AB:AM = 2:1, M is the midpoint of AB – (2)
- AC:AN = 2:1, N is the midpoint of AC – (3)
- From (1), (2), and (3), since Side – Angle – Side (SAS), △ABC∼△AMN
Thus, we can prove that △ABC∼△AMN. Also, since the similarity ratio of △ABC∼△AMN is 2:1, we know that the length of MN is half-length of BC.
Also, in similar figures, the angles are the same. In other words, ∠ABC = ∠AMN. If the corresponding angles are equal, the two lines are parallel. Therefore, BC||MN. Thus, we have also proved that BC and MN are parallel.
The Converse of Midpoint Theorem Is Also True
It is important to note that the converse of the midpoint theorem also holds. In other words, if BC||MN and $MN=\displaystyle\frac{1}{2}BC$, then point M and point N are the midpoints of the side. We can prove this as follows.

- In △ABC and △AMN
- ∠BAC = ∠MAN: Common angles – (1)
- ∠ABC = ∠AMN: Corresponding angles in parallel lines are equal – (2)
- From (1) and (2), since Angle – Angle (AA), △ABC∼△AMN
Also, since $MN=\displaystyle\frac{1}{2}BC$, the similarity ratio of △ABC∼△AMN is 2:1. From this fact, we know the following to be true.
- $AM=\displaystyle\frac{1}{2}AB$
- $AN=\displaystyle\frac{1}{2}AC$
Therefore, point M and point N are the midpoints of the side. Thus, we find that the converse of the midpoint connector theorem holds.
The Side Lengths Can Be Calculated from the Similarity Ratio Without Using the Midpoint
So far, we have explained the midpoints of a triangle. It is important to note, however, that the properties of the midpoint theorem can be used even if they are not midpoints.
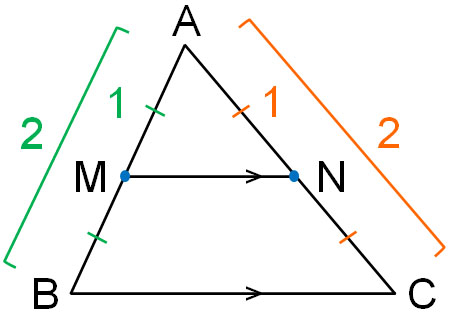
For example, suppose we take the following points of a triangle in the ratio of 1:2.
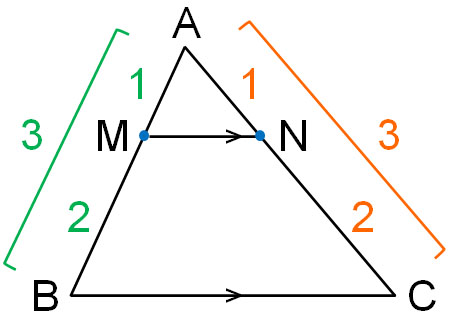
In this case, we have BC||MN and $MN=\displaystyle\frac{1}{3}BC$. The reason for this can be explained in the same way that we proved the midpoint theorem earlier. Even if they are not midpoints, the property of the midpoint theorem is still valid.
In similar figures, all side similarity ratios are the same. In this case, the similarity ratio of △ABC∼△AMN is 3:1. Therefore, if we know the length of one side, we can calculate the lengths of the other sides. For example, if the length of MN is 3 cm, the length of BC is 9 cm because MN:BC = 1:3.
Also, if two lines are parallel, the ratios of the sides will all be the same. For example, in the previous figure, AM:MB = 1:2. Also, AN:NC = 1:2.

For example, if the length of AM is 0.5 cm, the length of MB is 1 cm; if the length of AN is 0.7 cm, the length of NC is 1.4 cm. In a similar triangle, if the bases are parallel, the length can be calculated according to the ratio of the sides.
In Parallel Lines, Ratio of Line Lengths Is Same
After understanding these facts, you should be able to solve advanced problems. In the following figure for $l||m||n$, what is the value of $x$?

How do we solve this problem? In this situation, we do not know how to calculate $x$. So, let’s move the line as follows.
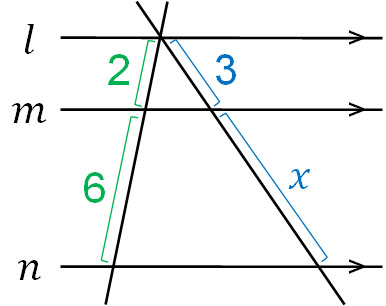
Moving the line does not change the length of the sides. Also, by moving the line in this way, we can create triangles. Since the triangle bases are parallel, we can use the properties of similarity shapes, as explained earlier.
We can calculate the value of $x$ by creating the following proportional relationship.
- $2:6=3:x$
Solving this proportional relationship, we get the following.
$2x=6×3$
$x=9$
Thus, we see that the value of $x$ is 9.
Calculating the Side Lengths of a Trapezoid
When we study similarity and the midpoint theorem, we may be asked to calculate the side length of a trapezoid as an advanced problem. For example, what is the length of $x$ in the following figure?

The figure is AD||MN||BC. Also, AM = MB and DN = NC, and we can use the midpoint theorem. However, since it is a trapezoid and not a triangle, it is not clear how to solve the problem.
So, let’s draw a line like the following.
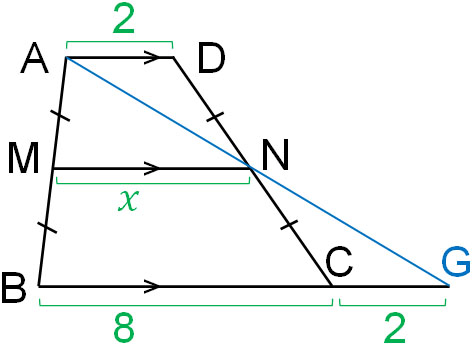
In this case, △ADN and △GCN are congruent. We skip the proof that they are congruent, but by using the theorem Angle – Side – Angle (ASA), we can see that the two triangles are congruent.
Since △ADN and △GCN are congruent, AD = CG = 2. In other words, the length of BG is 10. Also, △ABG is a triangle, and M and N are the midpoints of each side. Therefore, we can calculate the length of MN by using the midpoint theorem.
As mentioned above, the length of BG is 10. Therefore, we know that the length of $x$ is 5.
In the trapezoidal problem with parallel lines, we cannot solve the problem as it is. So, let’s make a triangle by moving the line or drawing a new line. Then you can use the midpoint theorem and the similarity property to find the side lengths.
Using the Midpoint Theorem in Quadrilaterals Creates Parallelograms
In mathematics, you may be asked to prove that a parallelogram can be created by using the midpoint theorem. You will be given the following figure, and you will have to prove that you can create a parallelogram by connecting the midpoints of the quadrilateral.
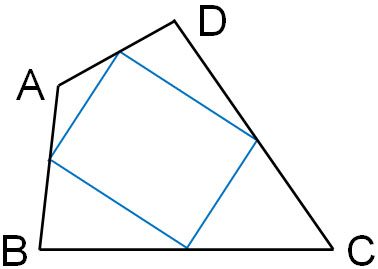
There are several conditions that satisfy a parallelogram. They are as follows.
- Two pairs of opposite sides are parallel to each other.
- Two pairs of opposite sides are equal in length.
- Two pairs of opposite angles are equal to each other.
- The diagonals intersect at their midpoints.
- One pair of opposite sides are parallel and equal in length.
In the proof of the parallelogram, we almost always use “One pair of opposite sides are parallel and equal in length “. In the proof of the parallelogram mentioned above, we can prove that it is a parallelogram by using “One pair of opposite sides are parallel and equal in length “.
When it comes to geometry problems in mathematics, we have to learn how to solve them. So, let’s understand how to think and prove it. First, draw a diagonal that will be AC, as shown below.
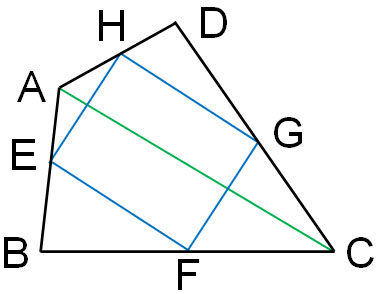
You can use either AC or BD diagonals. The procedure is the same for both, and we will use the diagonal AC.
Next, let’s focus on the two triangles. They are the following triangles.

Since H is the midpoint of AD, AH = HD. Also, G is the midpoint of DC, so DG = GC. Since two midpoints of a triangle are connected, the following is obtained from the midpoint theorem.
- HG||AC – (1)
- HG=$\displaystyle\frac{1}{2}$AC – (2)
Similarly, let’s consider the triangle on the other side.
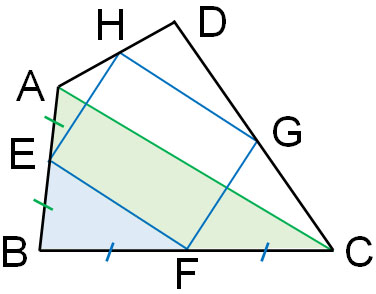
Since E is the midpoint of AB, AE = EB. Also, F is the midpoint of BC, so BF = FC. Since two midpoints of a triangle are connected, the following is obtained from the midpoint theorem.
- EF||AC – (3)
- EF=$\displaystyle\frac{1}{2}$AC – (4)
From (1) and (3), HG||EF. Also, from (2) and (4), HG = EF. We can prove that the quadrilateral is a parallelogram because one pair of opposite sides are parallel and equal in length.
Exercises: Midpoint Theorem and Similarity of Triangles
Q1: Given AB||CD||EF, calculate the value of $x$.
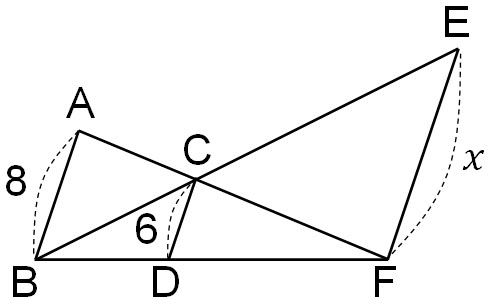
A1: Answer.
If we focus on △ABF and △CDF, the two triangles are similar. Therefore, we can see that the ratio of the sides is as follows.
For BD, DF, and BF, we don’t know the specific lengths of the sides. However, we can know the ratio of the sides. If we know the similarity ratio, we can get the value of $x$.
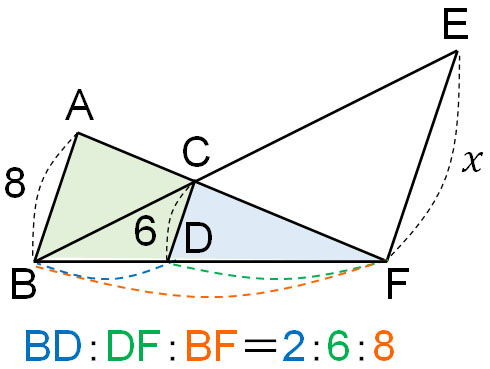
Next, let’s look at △BDC and △BFE; two triangles are similar. Also, the similarity ratio of △BDC and △BFE is 2:8 (1:4 to be exact) based on the ratio of the sides. Therefore, we can create the following proportional relationship.
- $2:8=6:x$
Solving this equation, we get $x=24$.
$2x=6×8$
$x=24$
Q2: For the trapezoid with AD||BC, M and N are the midpoints of the sides. Find the length of PO when AD = 6 and BC = 8 in the following figure.
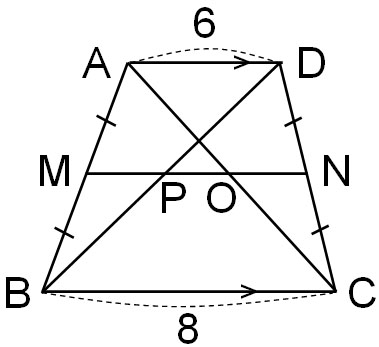
A2: Answer.
The length of MN can be calculated by the following method.
- $(8+6)×\displaystyle\frac{1}{2}=7$
The length of MN is 7. Also, since M and N are midpoints, P is the midpoint of BD. In the same way, O is the midpoint of AC.
So, let’s find out the length of PN; since the length of BC is 8, the length of PN is 4 according to the midpoint theorem. In other words, the length of MP is 3. In the same way, the length of MO is 4 according to the midpoint theorem. In other words, the length of ON is 3.
Since MP = 3, ON = 3, and MN = 7, the length of PO is 1.
- $7-3-3=1$
Calculating Lengths Using Parallel Lines
The midpoint connector theorem is a way to calculate the side lengths by using two midpoints of a triangle. In the midpoint theorem, the two lines are parallel, and the similarity ratio is 1:2.
The important thing is that even if they are not the midpoints, we can use the similarity ratio to calculate the side lengths. When two lines are parallel, the ratio of side lengths is equal to the similarity ratio.
In addition, the midpoint theorem and the concept of similarity can be used to calculate the side lengths not only for triangles but also for trapezoids using these properties. We can also use the midpoint theorem to prove why we can create a parallelogram inside a quadrilateral.
It is a calculation method that can be used under special conditions because the two lines need to be parallel. However, since the midpoint theorem is frequently used in mathematics, it is important to understand how to calculate the side lengths using similarity.