Math calculations frequently involve the use of letters instead of numbers. By using algebraic expressions, we can easily solve math problems.
One of the most important areas of algebraic expressions is linear equations. Linear equations are frequently used in daily life calculations and are the basis of mathematics. Even if there is a number you don’t know, you can find the answer by using a linear equation.
Equations have properties, and you need to understand their definitions and outlines. Also, if you can create linear equations by solving word problems, you will be able to use linear equations in your daily calculations.
How should we think about using linear equations? We will explain the properties of linear equations and how to solve them.
Table of Contents
Meaning and Definition of Equations
First, what is an equation? We have to understand the definition. If an equation contains numbers that we don’t know, an equation that uses the alphabet is called an algebraic expression. By using letters, we can create an expression.
If you have learned how to calculate polynomials, you already understand expressions that use letters. In polynomials, you can substitute numbers into $x$ to get various answers. For example, substituting numbers into $3x+1$ gives the answer as follows.
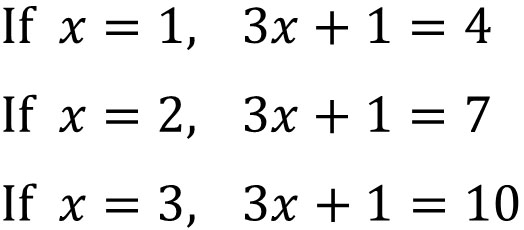
In linear equations, on the other hand, the answer can be right or wrong by substituting a number into the equation.
For example, if we have the equation $3x+1=10$, what will the answer be? If we apply various numbers to $x$, we get the following.
- $x=1, 3×1+1=10$: wrong
- $x=2, 3×2+1=10$: wrong
- $x=3, 3×3+1=10$: correct
We can’t substitute any number. Only a specific number can be used to get the answer. Because there is an equal sign ($=$) in the equation, the number of $x$ that satisfies the equation is limited.
Equal Sign in Equations Has Five Properties
In linear equations, there is always an equal sign ($=$). Since it means equal, we can use an equal sign if the two are equal. In addition, the following terms exist in the equation.
- Left side: the equation on the left.
- Right side: the equation on the right.
- Both sides: left and right sides

These words are used in linear equations.
It is important to note that the equals sign has five properties. Understanding the properties of equations containing the equals sign will enable us to solve problems with linear equations.
To understand the properties of equations, it’s easy to think of a balance. In equations, we use an equal sign. Therefore, the left and right sides must be equal. The equation is shown in the following figure.
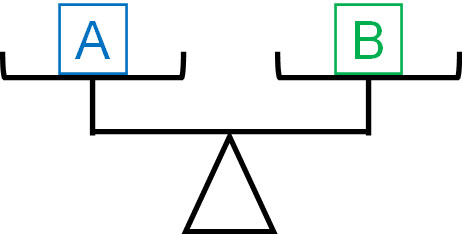
The left and right sides are equal by an equal sign. If $A=B$, then the following five things hold.
- Adding the same numbers, the equation holds.
- Subtracting the same numbers, the equation holds.
- Multiplying the same numbers, the equation holds.
- Dividing the same numbers, the equation still holds.
- Exchanging both sides, the equation still holds.
I will explain each of these.
-If $A=B$, then $A+C=B+C$
Why is it okay to add the same number to both sides? This is because if you add the same number to both sides, both sides will be equal. If we add the same thing, the balance will be equal as follows.
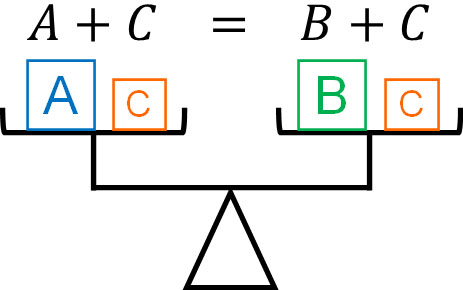
-If $A=B$, then $A-C=B-C$
In the equation, you can subtract the same number from both sides of the equation. You can subtract as well as add.
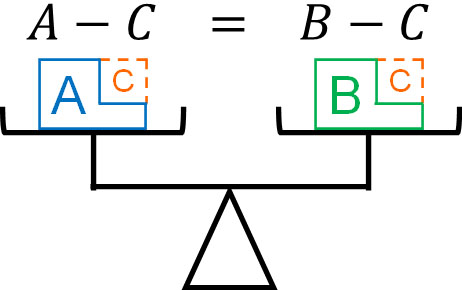
-If $A=B$, then $A×C=B×C$
In the equation, you can multiply both sides. This is because both sides of the equation are equal.

-If $A=B$, then $\displaystyle\frac{A}{C}=\displaystyle\frac{B}{C}$
If you divide both sides by the same number, the equation still holds. In algebraic expressions, we do not use division, but rather convert all division into multiplying fractions. Therefore, expressions are expressed as multiplying fractions, not dividing.
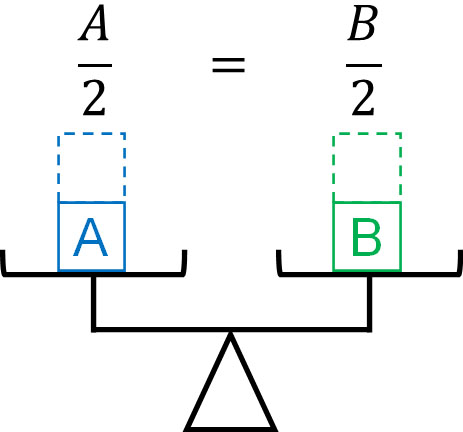
-If $A=B$, then $B=A$
If the equation holds, then it is okay to exchange the left and right sides. Since both sides are equal, they are equal even if they are exchanged.
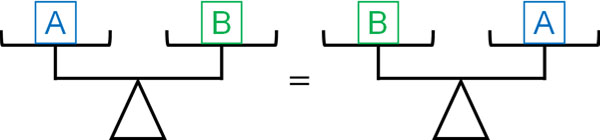
Some people may think that the properties of the equal sign that I have explained so far are obvious. However, this is understandable because we consider the example of a balance. On the other hand, if you are only given a formula such as “If $A=B$, then $A-C=B-C$,” you will not understand it.
When learning linear equations, many people have trouble understanding the properties of equations. So, let’s try to understand the properties of these equations through figures.
Solving Linear Equation Problems by Transposition
How do we solve the problem of linear equations? To do this, we use the property of equal sign explained earlier.
For both sides, you can add or subtract the same number and still get the same equation. For example, $x+2=11$ can be calculated in the following order.
- $x+2=11$
- $x+2\textcolor{red}{-2}=11\textcolor{red}{-2}$
- $x=11\textcolor{red}{-2}$
- $x=9$
In an equation, we can get the answer by adding or subtracting the same number on both sides.
However, in mathematics, we need to be able to calculate quickly. In fact, there is a time limit on the exam. So we use a technique called transposition. A transposition is a method of moving a number from the left side to the right (or right to left) by changing the sign.
For the previous calculation, we can omit equation (b), as shown below.

By transposition, we can eliminate the calculation process. As a result, miscalculation will be reduced. We all use transposition in algebraic expressions.
Transposition can be used not only with numbers but also with letters. We can transpose numbers and letters as follows.
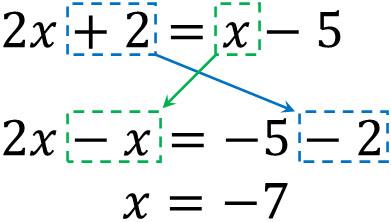
Also, we can multiply or divide the same number on both sides. By multiplying an integer or fraction, you get the value of $x$. For example, we get the following.
$3x=10$
$3x×\textcolor{red}{\displaystyle\frac{1}{3}}=10×\textcolor{red}{\displaystyle\frac{1}{3}}$
$x=\displaystyle\frac{10}{3}$
To answer a number we don’t know ($x$), we use a linear equation. Therefore, the final answer will be in the form $x=□$.
Note that we cannot transpose multiplication and division (multiplying fractions), unlike addition and subtraction. We need to calculate them by multiplying both sides.
Remove the Parentheses Using the Distributive Property and Convert to Integers
There are many equations that contain parentheses in algebraic expressions. In this case, you cannot transpose them. So we need to use the distributive property (or distributive law) and remove the parentheses first.
For example, how can we calculate $3(x-2)=14$? In this case, let’s remove the parentheses. We can calculate it as follows.
$3(x-2)=14$ : Distributive property
$3x-6=14$ : Transpose
$3x=14\textcolor{red}{+6}$
$3x\textcolor{red}{×\displaystyle\frac{1}{3}}=20\textcolor{red}{×\displaystyle\frac{1}{3}}$ : Multiplying fractions
$x=\displaystyle\frac{20}{3}$
Because you remove the parentheses, you can add or subtract by transposition. To solve the equation, use the distributive law to remove the parentheses first.
-Change Decimal to Integer by Multiplying Both Sides
In some cases, the multiplication of both sides of an equation is used to simplify the calculation. In equations that contain decimals or fractions, it is often necessary to multiply both sides of the equation.
For example, how do we calculate the following equation?
$0.04x-0.12=0.02x-0.2$
You can calculate the equation as decimals, but there is a high probability that a miscalculation will occur. So let’s simplify the equation by changing it to integers. In the previous expression, multiply both sides by 100.
$0.04x-0.12=0.02x-0.2$
$(0.04x-0.12)\textcolor{red}{×100}=(0.02x-0.2)\textcolor{red}{×100}$
$4x-12=2x-20$
$4x\textcolor{red}{-2x}=-20\textcolor{red}{+12}$
$2x=-8$
$x=-4$
Rather than calculating as decimals, it is easier if we convert them to integers.
-Changing Fractional Expressions to Integers
Fractions are also easier to calculate if they are converted to integers. For example, how do we calculate the following?
$\displaystyle\frac{2}{3}x-\displaystyle\frac{1}{4}=\displaystyle\frac{3}{8}x$
As with decimals, let’s change it to an integer expression by multiplying both sides. For example, we have the following.
$\displaystyle\frac{2}{3}x-\displaystyle\frac{1}{4}=\displaystyle\frac{3}{8}x$
$\left(\displaystyle\frac{2}{3}x-\displaystyle\frac{1}{4}\right)\textcolor{red}{×24}=\displaystyle\frac{3}{8}x\textcolor{red}{×24}$
$16x-6=9x$
$16x-9x=6$
$7x=6$
$x=\displaystyle\frac{6}{7}$
If you don’t convert the equation, it is difficult to calculate. In that case, we can use the property that equality holds even if we multiply both sides. By multiplying both sides by a number, we can convert the expression into an integer expression.
Understand the Difference Between Calculating Polynomials and Equations
It is important to note that polynomial problems and equations are different in properties. In polynomial problems, there is no equal sign. In contrast, equations have an equal sign, and the left and right sides are connected by equals.
Multiplying both sides of an equation is not a problem because it is an equation. Since equations have an equal sign, we can use the five properties explained earlier. However, if there is no equal sign, you cannot use them.
For example, the following calculation can be done by multiplying both sides by 100, as mentioned earlier.
- $0.04x-0.12=0.02x-0.2$
Since there is an equal sign, we can add, subtract, or multiply the same number on both sides. On the other hand, in the following equation, you cannot multiply by 100.
- $0.04x-0.02x-0.12+0.2$
If the equation does not contain an equal sign, you must calculate it as it is.
In typical polynomial calculations, only one expression exists. In contrast, in linear equations, there are two expressions on the left and right sides because of the presence of an equal sign. Therefore, the calculation method is different. Make sure you understand this difference to avoid calculation mistakes.
Tips on How to Solve Word Problems with Linear Equations
When learning linear equations, the most important thing is not to be able to solve calculation problems. The most important thing is to be able to create linear equations and answer them. This is because linear equations are used frequently in our daily lives.
For example, you need to use linear equations to calculate your electricity and water bills. Also, if you want to calculate how much your electricity bill has been reduced by saving on air conditioning, you can use the linear equation to calculate it.
You can also use the linear equation to know what time you need to leave your home to catch a plane or bus. If you make a mistake in your calculations, you will miss your flight or bus and not be able to travel.

In junior high school and high school, your parents will do all these calculations for you. However, if you are an adult, you have to do all the calculations by yourself. Linear equations are used in every situation. If you can solve linear equation problems, you will have no trouble in your life as an adult.
-How to Solve Linear Equations
How do we make linear equations? In algebraic expressions, we use alphabets to calculate the equation. The $x$ frequently used in algebraic expressions refers to an unknown number. A number you don’t know in math means that it is a number you want to answer.
For example, if you don’t know how many pens you need to buy, set the number of pens you need to buy to $x$. If you don’t know how many kilometers to walk, set the distance to walk to $x$ km. For all equations, set the number you don’t know to $x$.
Then make the equations and solve the problem. This way, you will be able to get the answer.
Expressing the Same Thing in Two Different Ways to Create Equations
When solving word problems, there is a right way. It is to make two equations. Since there is an equal sign, you use the equal sign to connect two things that have the same meaning.
For example, how do we make equations for the following word problem?
- How many pens costing \$2.00 each will cost you \$12.00?
Before learning algebraic expressions, we know that $12÷2=6$ and the answer is 6. Let’s express this in algebraic expressions.
Set the number you don’t know to $x$. In this problem, we don’t know how many pens we need to buy. So, set the number of pens we need to buy to $x$.
Then, as a result of buying $x$ pens that cost \$2 each, we will pay \$12. In other words, we can make the following equation.
- $\$2×x=\$12$
We make the equation by setting the number we want to find to $x$. The amount of money we buy $x$ pens at \$2 each must equal the total amount of money we pay (\$12). So we make an equation by connecting the two equations with an equal sign.
We have used a very simple equation to explain, but be aware of the following in the word problems of the linear equations.
- Set the unknown number to $x$.
- Create two expressions with the same meaning and connect them with an equal sign.
By doing this, you will be able to create equations. Then, solve the equation to get the answer.
Exercises: Solve Word Problems Using Linear Equations
Q1: Do the following calculation.
- $5(3x-3)+2=6x+3$
- $\displaystyle\frac{5x+2}{4}=\displaystyle\frac{-3x-3}{6}$
- $4-\displaystyle\frac{2x+3}{5}=0.4x$
A1: Answers.
In linear equations, we solve the problem by using transposition. However, if there are parentheses, you must remove the parentheses. And if there are decimals or fractions, you should simplify the equation by multiplying both sides of the equation.
(a)
$5(3x-3)+2=6x+3$
$15x-15+2=6x+3$
$15x-6x=3+15-2$
$9x=16$
$x=\displaystyle\frac{16}{9}$
(b)
$\displaystyle\frac{5x+2}{4}=\displaystyle\frac{-3x-3}{6}$
$\displaystyle\frac{5x+2}{4}\textcolor{red}{×12}=\displaystyle\frac{-3x-3}{6}\textcolor{red}{×12}$
$3(5x+2)=2(-3x-3)$
$15x+6=-6x-6$
$15x+6x=-6-6$
$21x=-12$
$x=-\displaystyle\frac{12}{21}$
$x=-\displaystyle\frac{4}{7}$
(c)
If both decimals and fractions are present in an expression, you should multiply both sides by the number that makes them whole numbers.
$4-\displaystyle\frac{2x+3}{5}=0.4x$
$\left(4-\displaystyle\frac{2x+5}{5}\right)\textcolor{red}{×5}=0.4x\textcolor{red}{×5}$
$4×5-\displaystyle\frac{2x+3}{5}×5=0.4x×5$
$20-(2x+3)=2x$
$20-2x-3=2x$
$-2x-2x=-20+3$
$-4x=-17$
$x=\displaystyle\frac{17}{4}$
Q2: Solve the following word problem.
Currently, the father’s age is 44, and the child’s age is 14. In how many years will the father’s age be twice the age of his child?
A2: Answers.
Set $x$ for the unknown number in the word problem. In this word problem, we don’t know how many years later the father’s age will be twice the age of his child. So we set the number of years that have passed to $x$.
After $x$ years have passed, the father’s age is $44+x$ years old. In contrast, the child’s age is $14+x$ years old. And by doubling $14+x$ years, it is equal to the age of the father. Therefore, the following equation holds.
- $44+x=(14+x)×2$
Solving this linear equation will give us the correct answer.
$44+x=2(14+x)$
$44+x=28+2x$
$x-2x=28-44$
$-x=-16$
$x=16$
-Reviewing the Answer
In linear equation word problems, we can check if the answer is correct or not by using the answer we get. The trick to solving the problem is to check whether the answer you get is really correct or not.
In this calculation, $x=16$. So, let’s apply for the number. The father’s age after 16 years will be $44+16=60$, while the child’s age will be $14+16=30$. Multiplying 30 by 2 gives us 60, so we can be confident that $x=16$ is the correct answer.
In linear equation word problems, you can check if a miscalculation is occurring by reviewing the equation in this way.
Q3: Solve the following word problem.
You are thinking of purchasing an item for \$5 each and selling it for \$8. However, 10% of the goods you purchased are defective and have scratches on the surface that make them look bad, so you sell them for \$6. How many items do you need to purchase and sell in order to earn a profit of \$140?
A3: Answers.
In this question, you do not know how many products you need to purchase and sell. So, the number of goods to be purchased is $x$.
It is important to note that the number of regular products is not $x$ pieces. There are also defective products with scratches in the mix. When we stock $x$ pieces, the number of defective products is $0.1x$ pieces. We need to subtract the number of defective products from the goods we purchased, so the number of regular products is $(x-0.1x)$ pieces.
Also, if we sell 1 piece of the regular product, our profit is $8-5=\$3$. On the other hand, if we sell one defective item with a scratch, the profit is $6-5=\$1$. Selling all of these results in a profit of \$140. Therefore, we have the following equation.

$3x×0.9x+1×0.1x=140$
$2.7x+0.1x=140$
$2.8x=140$
$2.8x×10=140×10$
$28x=1400$
$x=\displaystyle\frac{1400}{28}$
$x=50$
-Reviewing the Answer
In the same way, be sure to apply your answer and review it. Fifty products are purchased, the number of defective products is $50×0.1=5$ pieces. On the other hand, the number of regular products is $50-5=45$ pieces.
As already described, if we sell one regular product, our profit is \$3. If we sell one defective product, the profit is \$1. Therefore, the profit amount can be calculated as follows.
- $3×45+1×5$
If we calculate this equation, we get \$140. Therefore, we can see that we have made the equation correctly, and we can get the answer.
Q4: Solve the following word problem.
We have 200 g of 14% saline solution. We want to make it a 20% saline solution by adding salt. How many grams of salt should be added?
A4: Answers.
An important factor in the saline solution problem is the fact that adding salt increases the number of grams of solution. Therefore, when adding salt, the equation must also take into account the weight of the adding salt itself.
The number we don’t know in this question is how many grams of salt to be added. So, set the amount of salt to be added to $x$ g.
200g of 14% salt solution contains $200×0.14=28$ g of salt. By adding $x$ g of salt to it, we make it a 20% saline solution.
On the other hand, how many grams of salt are in a 20% salt solution? Since $x$ g is added to 200g of saline solution, the weight of the solution after adding salt is $(200+x)$ g. Since the concentration of a saline solution is 20%, we can calculate the amount of salt in 20% saline solution by the equation $(200+x)×0.2$.
As a result, we can create two different equations. Both equations show the amount of salt in 20% salt solution.
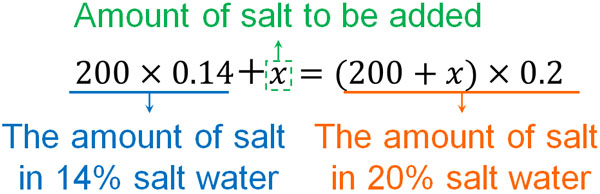
Solving this equation, we get the following.
$200×0.14+x=(200+x)×0.2$
$28+x=40+0.2x$
$x-0.2x=40-28$
$0.8x=12$
$0.8x×\displaystyle\frac{5}{4}=12×\displaystyle\frac{5}{4}$
$x=15$
-Reviewing the Answer
After answering the equation, let’s review it. To do this, make a different equation. 200 grams of 14% salt water contains $200×0.14=28$ g of salt. 15 g of salt is added to the solution resulting in $28+15=43$ g of salt.
If a salt water with a concentration of 20% contains 43 g of salt, how many grams of salt solution is in total? If the weight of the salt water is $y$ g, we have the following equation.
- $y×0.2=43$
Solving this equation gives us the following.
$y×0.2=43$
$y×0.2\textcolor{red}{×5}=43\textcolor{red}{×5}$
$y=215$
A 14% salt water is 200g, and if we add 15 g of salt to this, we get 215 g of salt water. The numbers match $y=215$. So we can see that we have made the equation and calculated it correctly.
It Is Important to Solve Problems with Linear Equations
The reason why we need to learn algebraic expressions in mathematics is to be able to create equations. Linear equations are used in all aspects of daily life. Therefore, if you don’t understand linear equations, you will often have trouble calculating them when you live as an adult because you can’t make the correct equations.
In linear equations, make sure you understand the properties of the equal sign. There are five properties of the equal sign, and all of us use these properties in mathematical calculations to get the answer.
Another important part of linear equations is being able to solve word problems. The ability to solve word problems allows us to apply mathematics to our daily lives. Consider an unknown number as $x$ and try to make two equations.
In addition, you can review the linear equation word problems as we have discussed so far. Reviewing them will help you to notice miscalculations, so be sure to review your answers to see if they are correct. If you understand these tips for solving equations, you will be able to reduce miscalculations in mathematics.