In the square root, we learn multiplication and division. In general, in mathematics, we learn addition and subtraction first. However, in the case of square roots, multiplication and division are easier. All you have to do is multiply the numbers in the root symbol.
However, there are rules for multiplying square roots. And few people understand why it is okay to multiply numbers in the radical symbol by each other. You have to learn about square root multiplication and division, including the reasons why.
Also, there is a method of calculation that is unique to square roots. That is prime factorization. Prime factorization makes the calculation easier and gives us the correct answer. In square root multiplication and division, we have to learn prime factorization at the same time.
In square root multiplication, we have to learn a new concept. We will explain how to multiply and divide square roots.
Table of Contents
How to Multiply and Divide Square Roots
In square roots, as mentioned earlier, we learn multiplication and division before addition and subtraction. Why do we learn multiplication first in square roots? The reason is that multiplication between square roots is easy to perform. The numbers in the root symbol can be multiplied.
In the case of multiplication of the root sign, the formula is as follows.
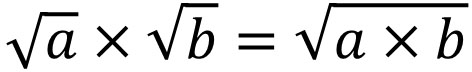
So, for example, the calculation is as follows.
- $\sqrt{2}×\sqrt{3}=\sqrt{6}$
- $\sqrt{7}×\sqrt{11}=\sqrt{77}$
Also, a division is the same as multiplication. This is because division can be converted to multiplying fractions. Since square roots can be multiplied by each other, the numbers in the radical symbol can be divided in the same way.
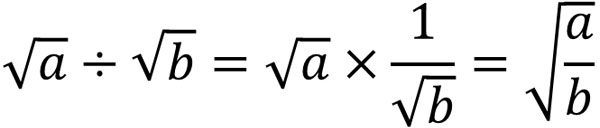
Therefore, we calculate the division as follows.
- $\sqrt{21}÷\sqrt{3}=\sqrt{7}$
- $\sqrt{15}÷\sqrt{5}=\sqrt{3}$
In multiplication and division between square roots, we can do normal multiplication and division. The only difference is whether there are root signs or not.
Multiply or Divide Integers and Square Roots Separately
The important thing is to separate integers and square roots for multiplication and division. Integers and square roots are completely different numbers.
In the square root, it is described as $3\sqrt{2}$ and so on. This is a multiplication of 3 and $\sqrt{2}$, which has the same meaning as $3×\sqrt{2}$. However, since the basic rule is to omit the $×$, so it is written as $3\sqrt{2}$.
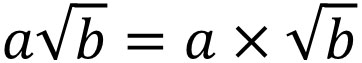
Because the numbers (integers) in front of the radical sign are considered separately, the integers and the square root have to be multiplied separately. In short, it is as follows.
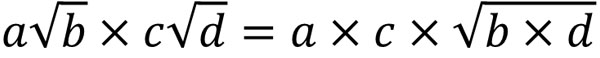
Integers multiply with integers. Square roots, on the other hand, multiply with square roots. Integers are never multiplied by square roots. In multiplication and division, integers and square roots should be completely separated.
So, for example, we have the following.
- $3×\sqrt{2}=3\sqrt{2}$
- $2×4\sqrt{2}=8\sqrt{2}$
- $2\sqrt{2}×3\sqrt{5}=6\sqrt{10}$

As you can see, the integer and the square root are calculated separately.
However, integers can be changed to square roots; we can convert integers to square roots by squaring them. For example, $2=\sqrt{2^2}=\sqrt{4}$. In the same way, $3=\sqrt{9}$. Also, $4=\sqrt{16}$.
We can’t multiply and divide an integer by a square root. So if we change the integer to a square root, we can multiply and divide the square roots by each other. For example, how can we solve the following problem?
- $\displaystyle\frac{\sqrt{12}}{2}$
$\sqrt{12}$ and 2 cannot be multiplied or divided. So, let’s use the root sign to represent 2. Since $2=\sqrt{4}$, we can calculate as follows.
- $\displaystyle\frac{\sqrt{12}}{2}=\displaystyle\frac{\sqrt{12}}{\sqrt{4}}=\sqrt{3}$
You cannot multiply an integer by a square root. However, integers can be converted to square roots. So to be more precise, by converting an integer to a square root, you can multiply and divide an integer by a square root.
Why Can We Multiply and Divide Between Square Roots
Why is it possible to multiply and divide root signs by each other? Few people understand this reason.
To understand this reason, we use a linear equation. Linear equations have the property that it does not matter if both sides are multiplied by the same number. For example, suppose we have the following balances.
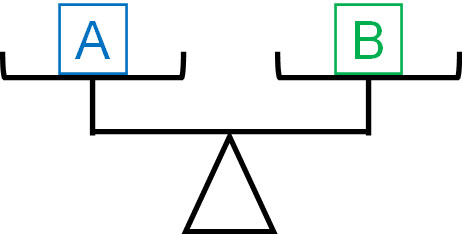
If two are the same, they are equal no matter how many times both sides are multiplied.

To understand why the multiplication of the square root is valid, let’s review the properties of linear equations.
-Prove Why Multiplication of the Square Root is Valid
Next, let’s prove why it is possible to multiply and divide square roots when calculating square roots. So let’s consider a situation where we multiply $\sqrt{a}$ and $\sqrt{b}$.
First, we square $\sqrt{a}×\sqrt{b}$. Don’t think, “Why are we squaring it?” Anyway, squaring it. What happens when you square it? Since it is multiplication, the meaning is the same whether there are parentheses or not. In multiplication, the parentheses can be removed at will.
For example, the following calculations have the same answer.
- $(2×3)×4=2×3×4$
This is called the associative property. Thus, the square of $\sqrt{a}×\sqrt{b}$ can be calculated as follows.
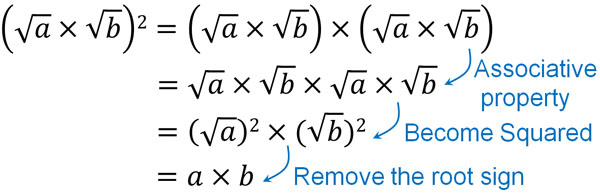
Thus, $\left(\sqrt{a}×\sqrt{b}\right)^2=a×b$.
Next, let’s convert this equation. First, we squared $\sqrt{a}×\sqrt{b}$. Then, return to the original state. Specifically, let’s add the root symbol to both sides.
A power is a type of multiplication. Also, integers can be converted to square roots by powering them. In other words, converting an integer to a square root is a kind of multiplication. In an equation, we can multiply both sides of the equation by the same number. Let’s take advantage of this property and add the radical sign to both sides. In this way, we get the following.

Thus, we have proved that $\sqrt{a}×\sqrt{b}=\sqrt{a×b}$. We can prove that we can multiply and divide square roots by using our previous knowledge of mathematics.
Use Prime Numbers and Do Prime Factoring
Note that the numbers in the radical symbol need to be as small as possible. How can we do this? We can make the square root by squaring the integer. Similarly, if there is a square in the root sign, we can convert it to an integer and then take it out of the root symbol.
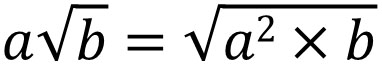
Not only can we make a square root from an integer, but we can also make an integer from a square root. For example, we have the following.
- $\sqrt{12}=\sqrt{2×2×3}=\sqrt{2^2×3}=2\sqrt{3}$
How can we efficiently find powers in the root symbol? The method is prime factorization. Prime factorization is the process of dividing using prime numbers.
Numbers have prime numbers. A prime number is a number that is divisible only by 1 and its number. Prime numbers include, for example, the following.
- Prime numbers: 2, 3, 5, 7, 11, 13, 17, 19
For example, there are only two divisors of 7: 1 and 7. Likewise, there are only two divisors of 11: 1 and 11. Dividing by any other number does not result in an integer. On the other hand, 4 has 1, 2, and 4 as its divisors; not only 1 and 4, but 2 is also a divisor. Therefore, 4 is not a prime number.
We can convert an integer (natural number) into a multiplication equation by dividing it using prime numbers. Understand that the reverse of multiplication calculation is prime factorization.

When it comes to prime factorization, the term is difficult to understand. However, the concept of prime factorization is simple if you understand it as a way to decompose numbers into multiplication expressions. Prime numbers cannot be further divisible. So, by using prime numbers, we can convert them into multiplication.
How to Do Prime Factorization? Steps to Multiply
How to do prime factorization? As an example, let’s try to factor 300 into prime numbers.
The way to do this is to divide the numbers in order, starting from the smallest prime number. The smallest prime number is 2. So, let’s divide 300 by 2. If we divide 300 by 2, we can divide it into 2 and 150. $300=2×150$.
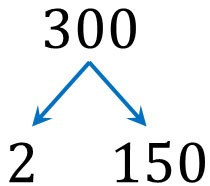
This method allowed us to do one prime factorization. However, 150 is not a prime number. It can be further divided by a prime number. So, let’s divide it again by a prime number. Dividing by 2, we get the following.
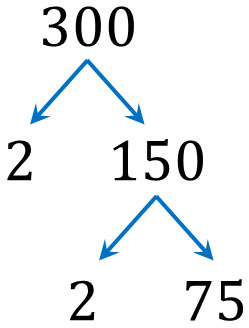
For 300, divide it twice by 2 to get 75. In other words, $300=2×2×75$. However, 75 is not a prime number. So, let’s do more prime factorization.
75 is not divisible by 2. So, we divide by 3.
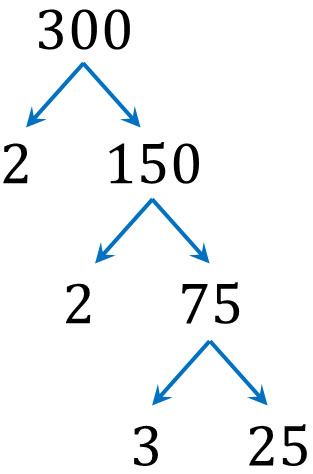
The result is $300=2×2×3×25$. Proceeding with the prime factorization in the same way, since 25 is not a prime number, we can divide it by 5. Thus, we get the following.
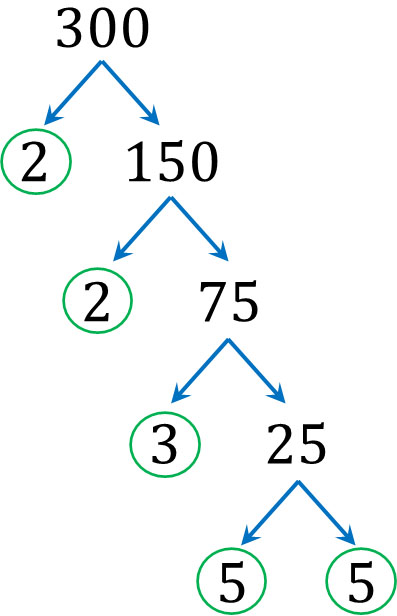
Dividing by the prime numbers, we finally found the following facts.
- $300=2×2×3×5×5$
Since 5 is a prime number, it cannot be further divided. In prime factorization, stop the division when a prime number appears at the end. After that, we collect all the prime numbers we have divided and the last prime number that appears. Since multiplying all the prime numbers in the circle in the figure above to get 300, the prime factorization is completed.
-The Symbol for Prime Factorization
When we actually do prime factorization, we have to calculate it efficiently and quickly. Therefore, we almost never use arrows to do prime factorization, as shown above. Instead, we use the following symbol.

To use it, write an integer (natural number) inside the symbol. Also, write the prime number to the left of the symbol. It looks like this.
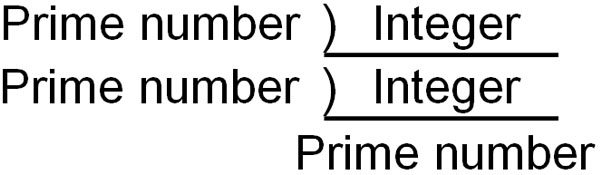
The usage is the same as in the previous arrow figure. We decompose an integer by dividing it with prime numbers. For example, the prime factorization of 300 looks like this.
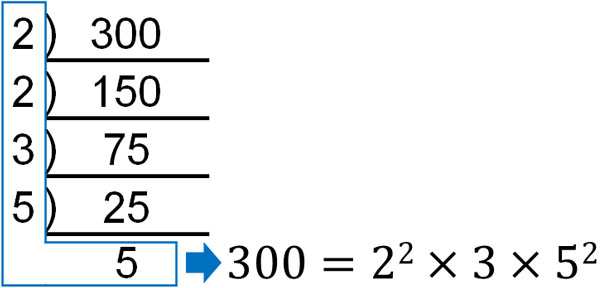
If a prime number appears at the end, the prime factorization is complete. Then, by collecting all the prime numbers, we can make a multiplication equation. The meaning is the same as the arrow figure. The difference is that by using this symbol, we can do prime factorization more efficiently.
The Answer to Prime Factorization Is the Same in Any Order
By the way, prime factorization can be calculated in any order because the final answer will be the same. For example, the prime factorization of 300 will give the same answer even if the order of division is different, as shown below.
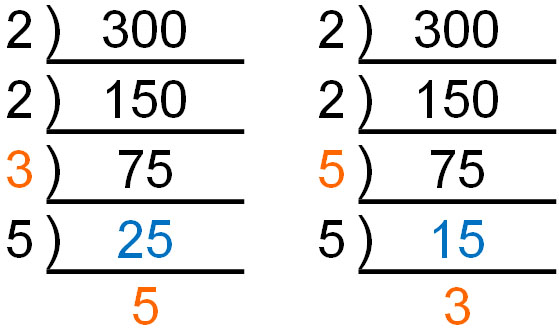
Earlier, we explained that in prime factorization, we divide the numbers starting from the smallest prime number. This is because the smaller the prime number, such as 2 or 3, the easier it is to divide, and the fewer mistakes are made. However, in some cases, it may be better to divide by a larger prime number to avoid miscalculation.
If the integer we want to divide is an even number, we can always divide it by 2. On the other hand, if it’s an odd number, it’s sometimes unclear if we can divide it by a smaller prime number.
For example, what prime number can you divide 105 by? 105 can be divided by 3. However, it is difficult to notice that it is divisible by 3. On the other hand, it’s easy to notice that 105 is divisible by 5.
The knowledge we can do prime factorization in any order can prevent miscalculation in mathematics. By using prime factorization, we can change an integer to a multiplication equation. In this case, don’t worry about the order in which you divide by prime numbers.
Take Out the Square Number in the Radical Symbol
Why do we need to learn prime factorization? It’s because we use prime factorization a lot in the calculation of the square root.
In the calculation of square root, there is a rule that the number in the root symbol must be as small as possible. In order to do so, we have to do prime factorization. Specifically, we have to take out the squared numbers in the root symbol.
As mentioned earlier, if there are squares in the radical symbol, we can put the number outside the root sign.
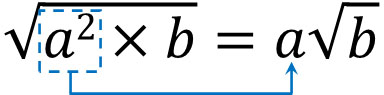
By using this formula, we can put the numbers in the root sign out after prime factorization. For example, we have already calculated that by prime factoring 300, we get the following.
- $300=2×2×3×5×5=2^2×3×5^2$
So how can $\sqrt{300}$ be calculated? Consider $\sqrt{300}$ as follows, and put the number outside the radical sign.

The reason for learning prime factorization is that it is used in square root calculations. When we take the numbers inside the root symbol out, we all do prime factorization.
So why do we need to take the numbers in the radical symbol out? The reason is simple: it’s easier to understand the numbers. For example, the number $\sqrt{300}$ is difficult to answer instantly. On the other hand, in the case of $10\sqrt{3}$, it is easy.
$\sqrt{3}≈1.73$. Since it is 10 times this value, we know that $10\sqrt{3}$ is about 17.3. Mathematics is the study of understanding what numbers mean. We have to make the numbers easy to understand, so we have to take the numbers out of the root symbol.
Do not Divide Other Than Prime Numbers
Note that in prime factorization, we should not use non-prime numbers for division. If we mix non-prime numbers, we can’t take out the numbers in the radical sign. For example, when we do prime factorization of 300, what happens if we divide it by 4?
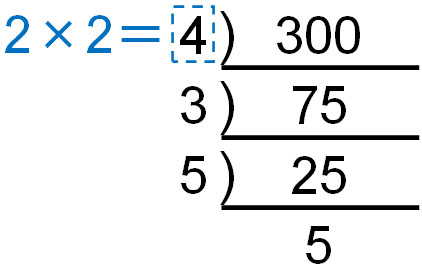
4 is not a prime number because it can be divided by 2. However, if we divide by 4, many people make the following equation.
- $\sqrt{300}=\sqrt{3×4×5^2}$
As a result, we end up with an answer of $5\sqrt{12}$. This answer is wrong because we can make the number in the root symbol even smaller.
For a non-prime number, such as 4, we can divide it by another number. As a result, we can’t change to a multiplication equation using the smallest number. Thus, the numbers in the root sign become larger and cause a calculation mistake. In prime factorization, be sure to divide by prime numbers.
Learn How to Multiply and Divide Square Roots
There are many times when we need to multiply or divide two square roots. In such cases, prime factorization makes it easier to put numbers outside the square root.
For example, how can we calculate the following?
- $\sqrt{15}×\sqrt{21}$
Prime factorizing 15 is $3×5$. Also, prime factorizing 21, it is $3×7$. Therefore, we can calculate as follows.
$\sqrt{15}×\sqrt{21}$
$=\sqrt{3×5}×\sqrt{3×7}$
$=\textcolor{red}{\sqrt{3}}×\sqrt{5}×\textcolor{red}{\sqrt{3}}×\sqrt{7}$
$=3×\sqrt{5×7}$
$=3\sqrt{35}$
When multiplying, prime factorization reveals that $\sqrt{15}$ and $\sqrt{21}$ contain $\sqrt{3}$ in the root sign, respectively; we can make 32, so we can get 3 out of the radical symbol. By prime factorizing, we can understand which numbers can be taken out from the root sign.
Note that if we cannot create powers, we cannot get the numbers out of the radical sign. In the previous calculation, the inside of the root sign is calculated as $\sqrt{5×7}=\sqrt{35}$. This is because although a square exists for 3, we cannot create a square for 5 and 7.
Perform a Prime Factorization of the Square Root First
By the way, in the multiplication and division of a square root, the first thing we should do is to make the numbers in the radical symbol smaller. In both multiplication and division, the smaller the number, the fewer calculation mistakes occur. For this reason, it is best to do prime factorization first in square root calculations.
For example, how can we reduce miscalculations in the following problem?
- $\sqrt{28}×\sqrt{18}$
There are two ways to calculate this as follows.

Checking the two calculation methods, it is obvious that the calculation is easier if you do the prime factorization first. Multiplication of 28 and 18 is complicated. Also, doing the prime factorization of 504 is hard.
Therefore, you should always do the prime factorization first, whether it is multiplication or division. That way, you will make fewer miscalculations.
Exercises: Square Root Multiplication and Division
Q1: Do the following calculations.
- $2\sqrt{3}×4\sqrt{21}$
- $\sqrt{15}×\sqrt{30}$
- $\sqrt{75}÷2\sqrt{3}$
- $(3+\sqrt{5})(3-\sqrt{5})$
A1: Answers.
(a)
$2\sqrt{3}×4\sqrt{21}$
$=2\sqrt{\textcolor{red}{3}}×4\sqrt{\textcolor{red}{3}×7}$
$=2×4×3×\sqrt{7}$
$=24\sqrt{7}$
(b)
$\sqrt{15}×\sqrt{30}$
$=\sqrt{\textcolor{red}{3}×\textcolor{blue}{5}}×\sqrt{2×\textcolor{red}{3}×\textcolor{blue}{5}}$
$=3×5×\sqrt{2}$
$=15\sqrt{2}$
(c)
If there is division, be sure to convert it to multiplying fractions.
$\sqrt{75}÷2\sqrt{3}$
$=\sqrt{3×5×5}×\displaystyle\frac{1}{2\sqrt{3}}$
$=5\textcolor{red}{\sqrt{3}}×\displaystyle\frac{1}{2\textcolor{red}{\sqrt{3}}}$
$=\displaystyle\frac{5}{2}$
(d)
In the calculation of the square root, we may use the factoring formula. The formula is following.
- $(x+a)(x-a)=x^2-a^2$
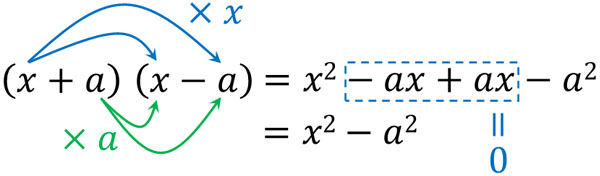
So let’s calculate the square root by using the formula $(x+a)(x-a)=x^2-a^2$.
$(3+\sqrt{5})(3-\sqrt{5})$
$=3^2-(\sqrt{5})^2$
$=9-5$
$=4$
Multiply the Square Root and Do Prime Numbers Calculation
Square roots calculation frequently involves multiplication and division. You can multiply and divide square roots by each other. The method is the same as normal multiplication. However, it is important to understand the rule of calculating integers and square roots separately.
Note that we must always do prime factorization when calculating the square root. We have to convert an integer into a multiplication equation. By doing prime factorization, we can get the numbers in the root symbol out.
Also, by doing prime factorization first, we can make the square root calculation easier. There are fewer calculation mistakes if we do prime factorization first. Let’s understand how to reduce miscalculation, including how to do it.
When you multiply and divide square roots, we have explained not only how but also why the calculation is done that way. By learning these, you will be able to perform mathematical calculations, including square roots.