When learning negative numbers, many people get confused. This is because when you multiply or divide different signs, the signs change. In addition, when you multiply negative by negative, the sign becomes positive. Why does this happen?
Few people can explain this reason. However, in order to understand mathematics, we need to solve the question beforehand.
Once you understand the signs in multiplication, you will be able to solve not only division and powers but also advanced questions in four arithmetic operations.
Many people find the calculation of negative numbers difficult because they do not understand the concepts. So, we will explain why the signs change with negative multiplication and how to solve the questions.
Table of Contents
Depending on the Sign, Multiplication Can Be Positive or Negative
When studying only positive numbers, there is no need to consider negative numbers. However, in mathematics, we have to deal with negative numbers.
In mathematics, there is multiplication and division. When multiplying, the sign of the answer will change depending on what sign is used. In multiplication, the result is as follows.
- Positive number $(+)×$ Positive number $(+)=+$
- Negative number $(-)×$ Positive number $(+)=-$
- Positive number $(+)×$ Negative number $(-)=-$
- Negative number $(-)×$ Negative number $(-)=+$
You might be thinking that you have to remember four of them. However, no need to remember these. It is as follows.
- Multiplication of same signs results in $+$.
- Multiplication of different signs results in $-$.
For example, $4×-3=-12$. This is because it is a multiplication of different signs. On the other hand, $-4×-3=12$. This is because it is a multiplication with the same signs.
But why is the answer negative if we multiply a positive number by a negative number? And why does multiplying a negative number by a negative number result in a positive answer? Few people can explain this reason correctly, so we’ll try to answer this question.
Why Is Multiplication by Plus and Minus Possible?
When multiplying, why do positive and negative answers become negative? Let’s solve this question first.
In general, when we solve this question, we think in terms of speed, time, and distance. The following formula exists.
- Speed $×$ Time $=$ Distance
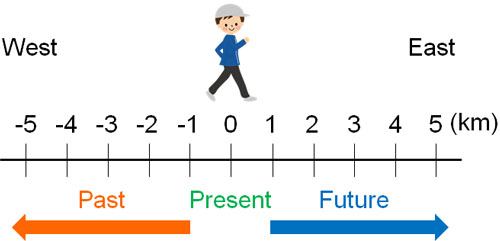
For example, if you walk at a speed of 1 km/h and 3 hours pass, you will have walked a distance of 3 km. Therefore, we can see that multiplication between positive numbers is valid.
-Why Is the Answer Negative for Different Signs?
Why does the use of different signs make the answer negative? The 0 (zero) represents a reference point. And if you use only positive signs, you are only considering the future. But in reality, the past also exists.
For the distance walked, we can make the following figure.
In this case, if you walk at -1km/h and 3 hours pass, where will you be? Walking at -1 km/h means that you are walking westward at a speed of 1 km/h. If you walk westward and 3 hours pass, you are at -3km.
- -1 km/h $×$ 3 hours $=$ -3 km
Also, if you walk at 1 km/h and -3 hours pass, where will you be? -3 hours have passed, which means 3 hours ago. If you walk eastward at a speed of 1 km/h, 3 hours ago you are at -3 km.
- 1 km/h $×$ -3 hours $=$ -3 km
If you think about it this way, you can understand why multiplying a positive number by a negative number results in a negative answer.
Why Multiplying a Negative Number by a Negative Number Makes a Positive
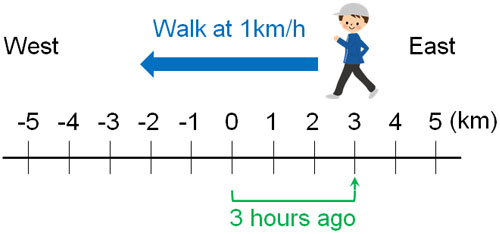
In contrast, why is multiplying a negative number by a negative number result in a positive number? As before, let’s consider the relationship between speed, time, and distance. If you walk at -1 km/h and -3 hours pass, where will you be?
Walking at -1 km/h means you are walking westward. Also – 3 hours have passed means that 3 hours ago.
If you are walking west (minus), then 3 hours ago, you are at +3 km (3 km to the east).
- -1 km/h $×$ -3 hours $=$ +3 km
This way of thinking allows us to see why the answer is positive when we multiply the negative by the negative.
The Signs Change for Division as well
We have explained multiplication so far. On the other hand, what about division?
We can think about the division in exactly the same way as multiplication. In short, if two numbers have the same sign, the answer will be the positive sign. On the other hand, if you divide by different signs, the answer will be a negative sign.
- Divisions with same signs result in $+$.
- Division with different signs results in $-$.
The reason for this is that both multiplication and division are the same. For example, if you walk at a speed of 1 km/h for 3 hours, you will walk 3 km.
- 1 km/h $×$ 3 hours $=$ 3 km
So, what is the speed per hour if you walk a distance of 3km in 3 hours? The equation and answer are as follows.
- 3 km $÷$ 3 hours $=$ 1 km/h
Thus, multiplication can be transformed into division.
For example, in a division of fractions, by reversing the top and bottom, the expression can be changed to multiplication. This is because division can be transformed into multiplication. Multiplication and division have the same properties. Therefore, the change in sign in a division is the same as in multiplication.
The Sign Changes Depending on Whether the Negative Number Is Even or Odd
However, when doing math calculations, it is rare to calculate only two numbers. Often, we multiply or divide multiple numbers. When multiplying several positive and negative numbers, what happens to the sign?
For this, when multiplying (or dividing), if the negative number is an even number, the sign of the answer will be positive. On the other hand, if the negative number is an odd number when multiplying (or dividing), the sign of the answer will be negative.
| Number of minuses | Equation | Answer sign |
| 1 (odd) | $+×-$ | $-$ |
| 2 (even) | $-×-$ | $+$ |
| 3 (odd) | $-×-×-$ | $-$ |
| 4 (even) | $-×-×-×-$ | $+$ |
| 5 (odd) | $-×-×-×-×-$ | $-$ |
As mentioned above, the negative has the opposite nature. The opposite of the opposite is positive. Therefore, if the negative number is even, the sign of the answer is positive. In contrast, if the negative number is odd, the sign of the answer is negative.
Not only integers but also decimals and fractions follow this rule. For example, the following is true.
- $-1×-1×-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{2}$
Since there are three negative numbers (an odd number of negative numbers), the answer will be negative. In multiplication and division calculations, the sign of the answer changes depending on whether the negative number is an even number or an odd number.
How to Calculate Power Using Exponent
For positive and negative numbers, the concept of power is as important as multiplication and division. Power is a calculation that shows how much of the same number is multiplied. In powers, for example, $3×3$ is expressed as 32. Also, $4×4×4$ is expressed as 43.
In terms of reading, 32 is 3 squared. 43 is 4 cubed.
- 32 = 3 squared (or 3 to the 2nd power)
- 33 = 3 cubed (or 3 to the 3rd power)
- 34 = 3 to the 4th power
- 35 = 3 to the 5th power
- 36 = 3 to the 6th power
The small number in the upper right corner is called the exponent. For example, for 43, 3 is the exponent. By checking the exponent, you can see how many times you need to multiply the same number.
Calculating powers using exponents, we get the following.
- $3^4=3×3×3×3=81$
- $(-2)^3=-2×-2×-2=-8$
- $0.1^2=0.1×0.1=0.01$
When calculating powers, be sure to check how many numbers you need to multiply by looking at the exponent.
Pay Attention to the Difference in Sign and Parentheses When Calculating Powers
When calculating powers, recognizing the difference between signs is the most important part of the answer. For example, what is the answer to the following power calculations?
- $-3^2$
- $(-3)^2$
- $-(-3)^2$
If you don’t understand the difference, you won’t be able to calculate the powers correctly. So, let’s learn the rules of exponents. Exponents have the following properties.
- Power to the previous number: the sign (-1) is not included
It is an exponent that does not include the sign and only powers the previous number. Therefore, -32 is calculated as follows.
- $-3^2=-1×3^2=-1×3×3=-9$
There is a -1 hidden in the -32. So let’s separate -1 and 32. The rule is that an exponent is only valid for the previous number and does not include the sign (-1).

However, we just explained earlier that $(-2)^3=-2×-2×-2=-8$. Even though exponents do not include signs, why do we multiply -2 three times in (-2)3? It is because of the use of parentheses.
In parentheses, the rule is that the equation in parentheses is considered to be a single number. In the case of (-2)3, there is a -2 inside the parentheses. If we consider -2 as a number, (-2)3 is $-2×-2×-2$. In the same way, (-3)2 becomes the following.
- $(-3)^2=-3×-3=9$
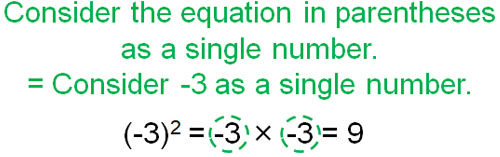
In contrast, how do we calculate -(-3)2? As mentioned earlier, exponents are only valid for the previous number. Also, the equation in parentheses is considered as a single number. Therefore, the equation is as follows.
- $-(-3)^2=-1×(-3)^2=-1×-3×-3=9$
The exponent of (-3) is 2. Therefore, we multiply -3 twice. In addition, we have to calculate -3 and the sign (-1) separately. The result is the equation shown above.
In Powers with Fractions, We Should Pay Attention to Parentheses
Depending on whether or not parentheses are present, the answer to the question varies greatly when calculating powers. It is important to pay attention to the parentheses, even for powers with fractions.
For example, what is the answer to the following question?
- $\displaystyle\frac{2^4}{3}$
- $\left(\displaystyle\frac{2}{3}\right)^4$
The exponent is only valid for the previous number. Therefore, consider the following.

In $\displaystyle\frac{2^4}{3}$, only 2 is to the 4th power. This is because the previous number is 2.
On the other hand, in $\left(\displaystyle\frac{2}{3}\right)^4$, $\left(\displaystyle\frac{2}{3}\right)$ to the 4th power, because there are parentheses in front of the exponent.
If there are no parentheses, only the number in front of the exponent can be calculated by powering. On the other hand, if there are parentheses, all the numbers inside the parentheses need to be calculated by powering. It is important to understand that in calculations using exponents, the method of calculation changes depending on whether there are parentheses or not.
Exercises: Math Multiplication, Division, and Power
Q1: Do the following calculation.
- $3×-4$
- $-30÷-5$
- $-4×-6×-3$
A1: Answers.
When multiplying or dividing using positive and negative numbers, the important thing to remember is that if the negative number is even, the answer is positive, and if the negative number is odd, the answer is negative. Therefore, the answers are as follows.
- $3×-4=-12$
- $-30÷-5=6$
- $-4×-6×-3=-72$
Q2: Do the following calculation.
- $-3^2×(-2)^2$
- $(-3)^3×8÷2^2$
- $-(-2)^4÷\displaystyle\frac{1}{3}×\left(-\displaystyle\frac{2}{3}\right)^2$
A2: Answers
When we solve a math question, we must first calculate powers. This is because powers are the same as a single number. For example, when solving the question $12÷2^2$, it is impossible to solve the question without first calculating 22. 22 is $2×2=4$, so $12÷4=3$.
In the same way, we need to calculate the powers first. Then we get the following.
- $-3^2×(-2)^2=-9×4=-36$
- $(-3)^3×8÷2^2=-27×8÷4=-54$
Consider the question in (c) as follows.
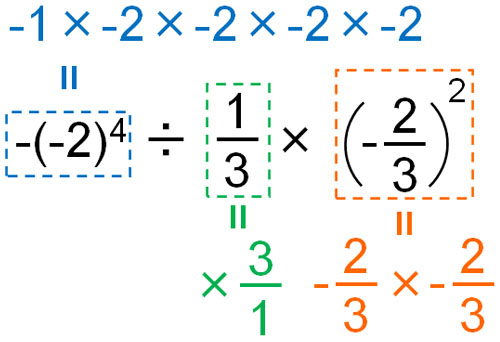
$-(-2)^4÷\displaystyle\frac{1}{3}×\left(-\displaystyle\frac{2}{3}\right)^2$
$=-16×3×\displaystyle\frac{4}{9}$
$=-\displaystyle\frac{192}{9}$
$=-\displaystyle\frac{64}{3}$
By calculating each one separately, we can finally make the equation for multiplication only.
Calculating Plus and Minus with Multiplication and Division
We can’t do math calculations unless we understand how to calculate plus and minus. So when you multiply and divide, learn how the signs work.
In particular, many people get confused when multiplying (or dividing) a negative number by a negative number because they don’t understand why it becomes positive. Therefore, we have explained why the answer is positive when multiplying a negative number by a negative number.
Also important is the fact that if the negative number is an even number, the answer is positive, and if the negative number is an odd number, the answer is negative.
In addition to that, you need to learn the concept of power. Parentheses are important in powers, and the answer depends on where the parentheses are placed. This is the concept of multiplication and division that you must learn with positive and negative numbers.