In mathematical space figures, there is a problem in calculating the volume and surface area of a pyramid or cone. Unlike prisms and cylinders, how can we calculate the volume and surface area of an object with a sharp-pointed?
Compared to prisms and cylinders, the calculation of pyramids and cones is more complicated. Especially when calculating cones, we have to understand new concepts.
Even so, if we already know how to calculate the volume and surface area of prisms and cylinders, we can find the volume and surface area of pyramids and cones. Although it is an advanced problem for prisms and cylinders, we can use our previous knowledge to answer the question while using the formula.
We will explain how to use the formulas and how to calculate the volume and surface area of pyramids and cones.
Table of Contents
Learn the Space Figures of Pyramids and Cones
There are two types of objects with a pointed tip: pyramids and cones.
In the case of cones, the base of the cone is a circle. On the other hand, pyramids can have a triangular or square base. In that case, it will be called a triangular pyramid or a quadrangular pyramid. It looks like the following.
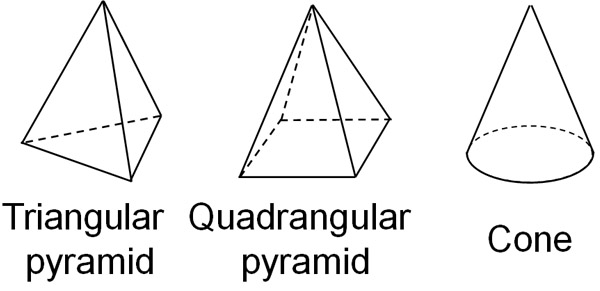
In any case, we must be able to calculate volumes and surface areas. It is a different method of calculation than for prisms and cylinders.
For the Volume of Pyramid and Cone, 1/3 Is an Important Number
First, we will explain how to find the volume. This is because it is easier to calculate than the surface area. How do we find the volume of a pyramid or cone?
We have already learned how to calculate the volume of prisms and cylinders. Here is the formula.
- The volume of a prism or cylinder = Base area × Height
If we know the base area and height, we can calculate the volume of a prism and cylinder by multiplying each number. The formula for the volume of a pyramid and cone is similar to this one. In the same way, multiply the base area and the height. Then, by reducing it by a third, we get the volume.
In other words, the formula to get the volume of a pyramid and cone is as follows.
- The volume of a pyramid or cone = Base area × Height × $\displaystyle\frac{1}{3}$
For example, what is the volume of the following triangular pyramid?

If we apply the formula to produce the volume of a pyramid and cone, it looks like this.
- $5×3×\displaystyle\frac{1}{2}×10×\displaystyle\frac{1}{3}=25$
Thus, we can calculate that the volume is 25 cm3. The way to calculate the volume of a pyramid or cone is to multiply the volume of a prism or cylinder by 1/3.
Why Does the Volume of a Pyramid/Cone Multiply by 1/3
Why does dividing a pillar shape into three equal parts result in the volume of a pyramid or cone? This can only be proven using high school math integration. At least, we cannot prove it in elementary or junior high school mathematics.
Therefore, you should try to prove why the volume of a pyramid or cone becomes 1/3 when you learn integrals in high school mathematics.
On the other hand, in elementary and junior high school math, how can we explain why we multiply by 1/3? To explain this, let’s assume the following figure is a cube and divide it into three parts.
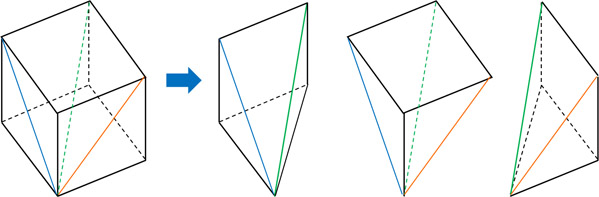
If we divide the cube into three quadrangular pyramids, we get this. It is important to note that all three quadrangular pyramids are the same shape. Since they have the same shape, they all have the same volume. This is why we can intuitively understand that the volume of a pyramid is one-third.
Of course, this explanation is not possible with a cone. It’s only possible with a cube. To get more accurate proof, we need to learn integrals, which are studied in high school mathematics, as mentioned above.
But in any case, even if we don’t do the calculations, we can intuitively understand the volume of a three-dimensional object, even in elementary or middle school mathematics.
Surface Area of a Pyramid/Cone Is the Sum of Base Area and Side Area
On the other hand, how can we calculate the surface area of pyramids and cones? The idea is the same as how to calculate the surface area of prisms and cylinders.
When calculating the surface area of prisms and cylinders, we calculate the base area and the side area, respectively, and add them up. In the same way, for pyramids and cones, we need to find the base area and side area respectively, and add them up. Thus, we have the following formula.
- The surface area of a pyramid or cone = Bottom area + Side area
The base and sides of the pyramid and cone are as follows, respectively.

We cannot get the surface area by a single equation. By calculating the two, base area and side area, we can get the surface area of a pyramid or cone.
Generatrix Becomes a Radius of a Sector in a Cone
When figuring out the surface area of a pyramid, we have already learned how to calculate the base area and side area. We also understand the formulas for calculating the area of the triangles and rectangles. For example, the net of a quadrangular pyramid would look like this.

So, for a quadrangular pyramid, we can calculate the area of the rectangle (base) and triangle (sides).
On the other hand, how can we calculate the surface area of a cone? Cones have a generatrix. The following is the generatrix for a cone.
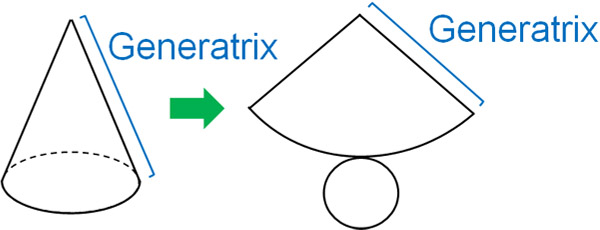
In the net of a cone, a circle and a sector are represented. The radius of the sector is the generatrix. Therefore, we should use the generatrix to give the sector area.
The sector area can be found by using the central angle. The formula for finding the sector area is as follows.

After finding the area of a circle, the sector area can be calculated by multiplying it by $\displaystyle\frac{central~angle}{360°}$. We can then calculate the surface area of the cone by adding the base area.
How to Find the Central Angle of a Cone from the Generatrix
On the other hand, if we don’t know the central angle, how can we calculate the side area of the cone? In this case, you should find the central angle of the cone from the generatrix.
For example, how can we calculate the central angle of the following cone?
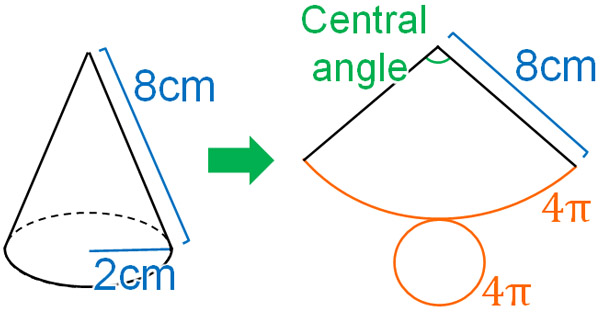
Considering the net of the cone, the radius of the sector is 8 cm. Also, the arc length and the circumference of the base of the cone are the same. The diameter of the base of the cone is 4 cm. Therefore, the length of the circumference (arc length of the sector) can be calculated as follows.
- $4×π=4π$
So, let’s apply the formula to produce the length of the sector arc. As with the area, the arc length of the sector can be calculated by figuring out the diameter of the circle and then decreasing the number according to the ratio of the central angle. The formula is as follows.

Using this formula, let’s get the central angle of a sector. The radius of the sector is 8 cm, so its diameter is 16 cm. And as mentioned earlier, the arc length of the sector is $4π$ cm. If we set the central angle as $x$, we can create the following equation.
- $16×π×\displaystyle\frac{x}{360}=4π$
Solving this equation, we get the following.
$16×π×\displaystyle\frac{x}{360}=4π$
$x=4π×360×\displaystyle\frac{1}{16π}$
$x=90$
Thus, we see that the central angle is 90°.
How to Calculate the Sector Area Without a Central Angle
If you calculate the central angle using the previous method, you can calculate the sector area. Then, by finding the base area, you can calculate the surface area of the cone.
However, calculating the area of the sector after finding the central angle is troublesome. Is there an easier way to calculate the surface area of a sector? There is a formula for calculating the area of a sector without a central angle. Here is the formula.
- Side area of the cone = Generatrix × Base radius × $π$
You can remember this formula. However, since it is a formula that is not used often, there is a high probability that you will forget it. So try to understand how to derive the formula. Once we learn how to make the formula, we will be able to get the area of a sector without remembering the formula.
The formula for finding the arc length and area of a sector is as follows.
- Arc length of the sector = radius $×2×π×\displaystyle\frac{central~angle}{360°}$
- Sector area = radius$×$radius$×π×\displaystyle\frac{central~angle}{360°}$
When comparing two formulas, don’t you think that they are similar? So, for the formula to find the arc length of a sector, let’s multiply both sides by radius$×\displaystyle\frac{1}{2}$. Then we get the following.

The arc length of the sector is equal to the length of the base circumference, as mentioned earlier. Therefore, it is the following.

Thus, we have proved that the following formula holds.
- Side area of the cone (sector area) = Generatrix × Base radius × $π$
The sector area has the same meaning as the side area of a cone. Even without a central angle, we can produce the side area of a cone in this way.
Exercise: Volume and Surface Area of Pyramids and Cones
Q1: Calculate the volume and surface area of the following cone. Let pi be $π$.

A1: Answers.
-How to find the volume of a cone
When figuring out the volume of a pyramid or cone, try to substitute the formula. First, calculate the base area. For the cone shown above, the base area is as follows.
- $3×3×π=9π$
We then substitute the numbers into the formula to get the volume of the cone.
- $9π×4×\displaystyle\frac{1}{3}=12π$
-How to find the surface area of a cone
Let’s calculate the base area and the side area separately. The base area of the cone is $9π$ cm2, as we just calculated.
On the other hand, how can we calculate the side area of the cone? One way to calculate the sector area is to calculate the central angle and then get the area. However, it is possible to get the sector area from the generatrix. Here’s the formula.
- Side area of the cone = Generatrix × Base radius × $π$
By substituting this formula, we can get the side area of the cone. It is as follows.
- $5×3×π=15π$
The side area of the cone is $15π$ cm2. The base area is $9π$ cm2, so let’s add them up.
- $15π+9π=24π$
If you forget the formula for the side area, you can derive the formula and calculate it. Or you can calculate the sector area after finding the central angle.
Memorize Formulas and Understand the Concept of Generatrix
When calculating the volume or surface area of a pyramid or cone, it is important to remember the formula. When figuring out the volume of a pyramid or cone, you can’t calculate the volume if you don’t remember the formula. You can get the volume of a pyramid or cone by multiplying the volume of a prism or cylinder by 1/3.
In contrast, for the surface area, find the side area and the base area, and add them up. You can figure out the area of each by considering the net.
In addition, the concept of finding the surface area of a cone is a bit more complicated. You have to understand the concept of a generatrix. The generatrix of a cone is equal to the radius length of the sector. By using this property, we can calculate the central angle and the area of the sector.
Once we learn these things, we can calculate the volume and surface area of a pyramid and cone. The volume and surface area of pyramids and cones are important in mathematical space figures, so let’s understand how to calculate them.