When you study mathematics, you may be taught about the commutative property (or commutative law) and the associative property (or associative law). The commutative property and the associative property are taught in elementary or junior high school.

The commutative property and the associative property are valid for addition and multiplication. The commutative property and the associative property cannot be established by subtraction and division. However, subtraction can be converted to addition, and division can be converted to multiplication. This means that we can use these rules in all calculations.

It is important to understand these rules in mathematics. Understanding the commutative property and the associative property will allow us to perform all kinds of calculations. Although we don’t use division anymore in math in junior high school and above, the commutative property and the associative property can help us understand why this is the case.

We will explain how to think about and apply the commutative law and the associative law.

An Overview of the Commutative Law and the Associative Law

What are the commutative property and the associative property that we learn in elementary or secondary school? They are as follows.

  • Commutative property: the law that gives the same answer even if the numbers are swapped.
  • Associative property: the law that gives the same answer even if you change the place of parentheses.

Regarding the commutative property and the associative property, both of which are used in so many situations, they are essential knowledge when solving math problems. These laws are used in addition and multiplication. But in practice, they can also be applied to subtraction and division.

In other words, we can use the commutative property and the associative property in all calculations. This makes it convenient, and these laws are useful for everyone, including those who do mathematical calculations in high school, college, and even in the business world.

In the Commutative Property, Swapping the Numbers Gives the Same Answer

In the commutative property, if you swap numbers, the answer will be the same. The commutative law is satisfied by addition.

For example, we have the following.

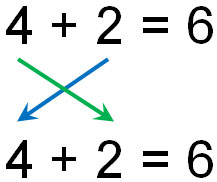
It doesn’t matter how you rearrange the order; this is called the commutative property of addition.

The same is true for multiplication. The commutative property is satisfied not only in addition but also in multiplication. As shown below, the answer is the same in multiplication, even if the numbers are swapped.

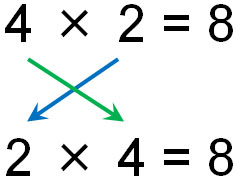
It doesn’t matter how you multiply, and this is called the commutative property of multiplication.

Isn’t the Commutative Property Established by Subtraction and Division?

However, it is said that the commutative law is not valid for subtraction and division. Let’s try to calculate by actually swapping numbers.

For example, if we swap the numbers in subtraction, we get the following.

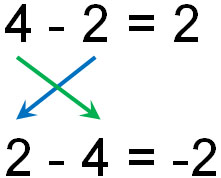
Thus, the answers are different. In one equation, the answer is 2, and in the other equation, the answer is -2. Since we subtract different numbers, the answers will naturally be different. This is the reason why it is said that the commutative property is not valid in subtraction.

The same is true for division. In the case of division, it is as follows.

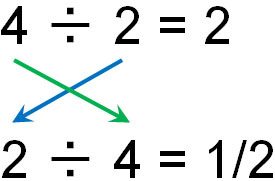
If we use the commutative property in division, the answer will change like this. Therefore, the commutative property is not valid in division.

Changing the Signs and Making Them Negative Numbers, the Commutative Property Is Established

If the commutative property is only valid for addition and multiplication, you may think that it is meaningless because its use is limited. However, the commutative law that we learn in elementary school or junior high school mathematics is very important.

Why is the commutative property so important even though it only applies to addition and multiplication? It’s because by changing subtraction to addition, the commutative property becomes valid. For division, the commutative property is also established by changing it to multiplication.

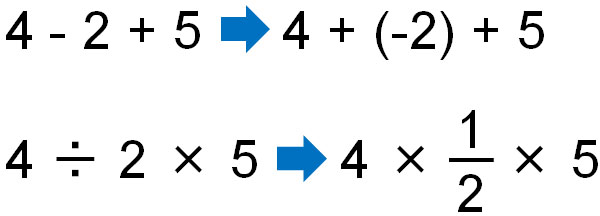
Addition and subtraction are the same. Subtraction can be converted to addition. For example, the following are all the same equations and the same answer.

  • $4-2=2$
  • $4+(-2)=2$

Once you learn positive and negative numbers, you can understand that addition and subtraction are the same.

As mentioned above, the commutative property is valid for addition. So, by changing subtraction to addition of negative numbers, the commutative law is established.

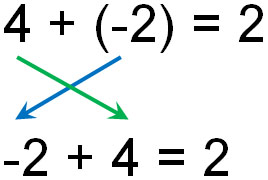
What is important is the fact that the commutative property is valid even for negative numbers. Earlier, we have explained that the commutative property is not established for subtraction. In fact, however, we can use the commutative property of addition even for subtraction because the commutative law is established by changing subtraction to addition.

-Use Fractions in Division and Use the Commutative Property

The same is true for division. By converting division to multiplication, we can use the commutative property of multiplication.

How do we convert division into multiplication? This is done by using fractions. By using reciprocal numbers, we can convert division into multiplying fractions, as shown below.

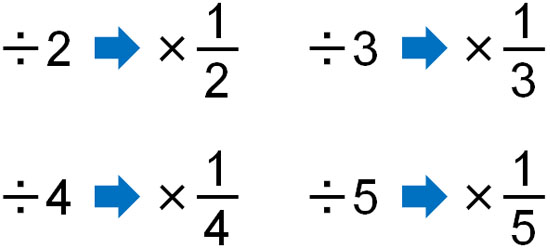
As mentioned above, the commutative property is valid in multiplication. As shown below, the answer is the same in multiplication, even if it is a fraction.

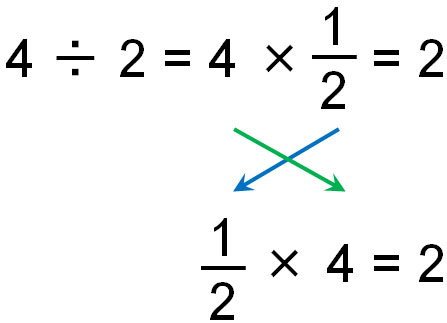
If you want to change subtraction to addition, you just need to change the plus and minus signs. However, in the case of division, you have to change it to fractions. This requires a bit of work. In any case, you can use the commutative property even in division.

The Associative Property, Which Allows You to Change the Place of Parentheses

When we learn the commutative property, we also learn the associative property. What kind of law is the associative law?

The associative property allows us to change the place of the parentheses freely. The same as the commutative property, the associative property is only valid for addition and multiplication. As shown below, the answer is the same even if we change the position of the parentheses in addition.

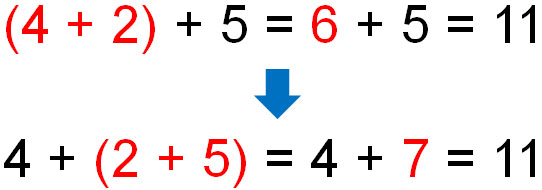
In mathematics, the rule is to calculate inside the parentheses first. It doesn’t matter where the parentheses are placed in addition.

In the same way, the associative property is valid for multiplication.

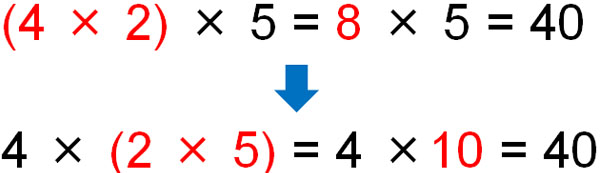
Why is the associative law valid? It is because the meaning is the same whether the parentheses are present or absent. The answer is the same even if you remove the parentheses as follows.

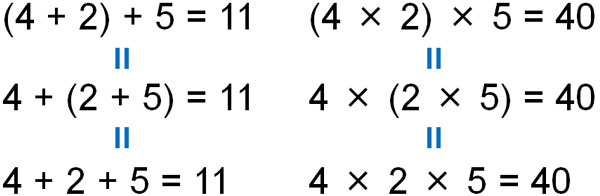
The answer is the same no matter where you put the parentheses because it doesn’t matter if there are parentheses or not. The associative property is just a law of the obvious.

The Associative Law Allows You to Calculate Anywhere You Want

The associative property is, in essence, a law that you can calculate anywhere you want. For example, when doing multiplication, you must have calculated the numbers in a different order. For example, how would you do the following calculation?

  • $2×6×13$

From left to right, the calculations are as follows.

  • $\textcolor{red}{2×6}×13=\textcolor{red}{12}×13=156$

You need to calculate $12×13$, which makes the calculation more difficult. So let’s use the associative property and change the order of the numbers. For example, instead of $2×6×13$, we change the equation to $6×13×2$. In this case, we get the following.

  • $\textcolor{red}{6×13}×2=\textcolor{red}{78}×2=156$

Thus, the calculation is easier; there are fewer calculation errors when multiplying numbers with fewer digits than when multiplying numbers with two digits.

The Formula for Subtraction and Division Are Established by Changing the Sign

The associative property is valid for addition and multiplication expressions. It is the same as the commutative property that cannot be applied to subtraction and division. For example, in subtraction, changing the parentheses will change the answer as follows.

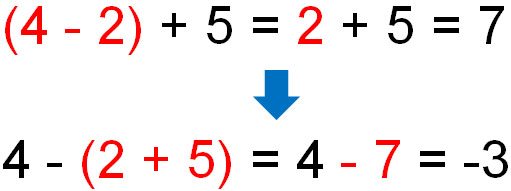
If there are parentheses in the equation, we must first calculate the inside of the parentheses. So when there is subtraction, the answer changes by using the associative property.

The same thing happens in division. The answer changes when the location of the parentheses changes, as shown below.

For subtraction and division, the associative property is not valid.

-Calculate by Addition or Multiplication

However, in practice, it doesn’t matter if there is subtraction or division. Just like the commutative property, subtraction can be converted to addition, and division can be converted to multiplication. The result is as follows.

It can be modified to an addition or multiplication equation so that the associative property is established. The answer is the same no matter where you put the parentheses. In other words, you can do the calculation from any place first.

In general, the associative property is not available for subtraction and division. However, by converting it to addition or multiplication equations, the associative law becomes valid. Therefore, the associative property is a rule that can be used in all calculations.

Use Multiplying Fractions Instead of Division in Math

Why do we need to understand the commutative property and the associative property, including in elementary school and junior high school math? This is because they are essential for easier calculations. Understanding the commutative property and the associative property is especially important for division calculations.

When you convert subtraction to addition, the method is simple. Just make the addition and then make it a negative number. It is as follows.

  • $2\textcolor{red}{-3}=2\textcolor{red}{+(-3)}$

For division, on the other hand, you can’t calculate it as it is. In order to change division to multiplication, you have to change it to multiplying fractions. By using reciprocals, we have to make the form change.

  • $2\textcolor{red}{÷3}=2\textcolor{red}{×\displaystyle\frac{1}{3}}$

By making the expression only multiplication, we can calculate from anywhere.

We don’t use division in maths in secondary school and above because the commutative property and the associative property are not valid. Instead, we calculate after converting division into fractions.

Also, in the case of division, there are many cases where the numbers are indivisible. With fractions, on the other hand, you can get an answer even if you can’t divide. It is important to understand that division is useless and is rarely used in mathematics.

The reason why all of us convert division to multiplication in secondary school and above in math is so that we can use the commutative and associative properties. This makes it much easier to calculate and less likely to make calculation errors.

Exercises: the Commutative and the Associative Property for Positive and Negative Numbers

Q1: Do the following calculation.

  1. $(6 ÷ 15) × 5$
  2. $-4 ÷ 3 ÷ 6 × 15$

A1: Answers.

For addition and subtraction, you can solve problems without trouble when you use the commutative law and the associative law. On the other hand, if a division is involved, you need to convert it to multiplying fractions. So use the reciprocals and turn them into fractions.

(a)

$(6\textcolor{red}{÷15})×5$

$＝(6\textcolor{red}{×\displaystyle\frac{1}{15}})×5$

$=6×\displaystyle\frac{1}{3}=2$

In division, we always convert it to multiplying fractions. Then, in this calculation, we calculate $\displaystyle\frac{1}{15}×5=\displaystyle\frac{1}{3}$ first. It’s easier to calculate than $6×\displaystyle\frac{1}{15}$.

(b)

$-4÷3÷6×15$

$=-4×\displaystyle\frac{1}{3}×\displaystyle\frac{1}{6}×15$

$=\textcolor{red}{-4×\displaystyle\frac{1}{6}}×\textcolor{blue}{\displaystyle\frac{1}{3}×15}$

$=\textcolor{red}{-\displaystyle\frac{2}{3}}×\textcolor{blue}{5}$

$=-\displaystyle\frac{10}{3}$

First, we convert division into multiplying fractions. Then, by using the commutative property and the associative property, the numbers are swapped to make the calculation easier.

Calculating with $-4×\displaystyle\frac{1}{3}$ and $\displaystyle\frac{1}{6}×15$ is difficult. It is also difficult to multiply two fractions.

On the other hand, $-4 × \displaystyle\frac{1}{6}$ and $\displaystyle\frac{1}{3} × 15$ allow you to reduce the number, making the calculation easier. In a multiplication-only equation, you can swap the numbers freely. In this way, we use the commutative law and the associative law.

Learn the Definition of the Law and Use it in Formulas

There are several laws in mathematics. One of those laws is the commutative property and the associative property. Why do we need to understand these rules? The reason is that the laws make it easier to calculate expressions and reduce calculation errors.

Some of the most important laws in mathematics that we all use are the commutative property and the commutative property. Even in elementary school math, we all use the commutative property and the commutative property.

However, in order to use the laws in mathematical formulas, we need to understand the rules and definitions. The commutative property and the commutative property are only valid for equations with addition or multiplication. So if there is subtraction or division, convert it to addition or multiplication. Note that subtraction is easy to change, but with division, you must change it to fractions.

Also, if you learn the commutative law and the associative law, you can understand why no one uses division in math in junior high school and above. Division is not useful. Be sure to use the reciprocal and convert it to multiplying fractions before doing the calculation.