A mathematical equation that uses the alphabet is an algebraic expression. In junior high school and high school math, we need to understand how to use algebraic expressions because they are almost always used in math.

An equation that consists of several algebraic expressions is called polynomials. In polynomial calculations, multiplication and division are frequently used. So we must understand not only addition and subtraction but also how to multiply and divide polynomials.

In order to understand this, we need to learn the distributive property (or distributive law). Understanding the distributive property is the key to being able to multiply and divide polynomials.

If you learn how to multiply and divide polynomials, you will also be able to perform substitution calculations. We will explain how to do polynomial multiplication, division, and substitution.

Expanding the Equation: Remove the Parentheses with the Distributive Law

There are several laws in mathematics. One of the most important laws is the distributive property. If you study mathematics, we all use distributive law.

Let’s understand that the distributive property is a rule that allows you to remove parentheses. Specifically, it is as follows.

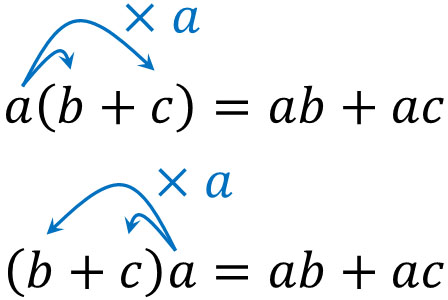
This is one of the most basic formulas and is frequently used in polynomial calculations. By using the distributive property, we can remove the parentheses and convert them into addition or subtraction equations.

Removing the parentheses is called expanding (or developing) in mathematics. When a math problem asks you to expand, it means to remove the parentheses by using the distributive property.

The Reasons Why the Distributive Property Established, Think in Terms of Area

Why does the distributive property hold? The reason for this is easy to understand if you think of it in terms of the sum of areas. The distributive property is taught in elementary school or junior high school mathematics. The reason why we learn it in elementary school is that we can explain the reason why the distributive law is valid by using a simple calculation of area.

When calculating the area of a rectangle, the following formula is used.

  • Vertical × Horizontal = Area

Therefore, the area of the two rectangles below can be calculated by the following formula.

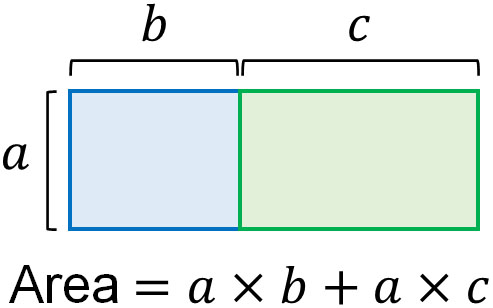
However, when calculating the area, it’s okay to add the horizontal length first. In other words, you can do $b+c$ first.

After doing $(b + c)$ to get the horizontal length, we multiply it by $a$, the vertical length. This method also gives us the total area of the two rectangles.

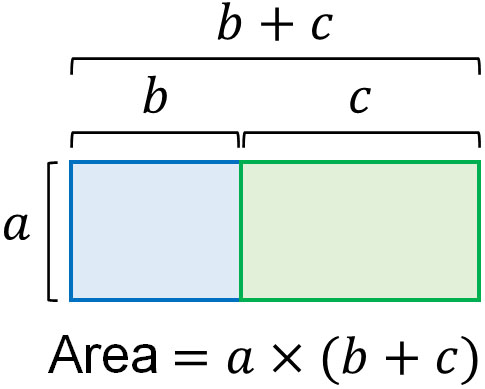
In other words, we see that the following formula holds.

  • $a(b+c)=ab+ac$

In mathematics for junior high school and above, we all use distributive law to develop equations. The reason why the distributive law is valid can be explained in elementary school math.

Use the Distributive Property in Algebraic Multiplication and Division

When multiplying with the alphabet, you need to understand the distributive law to be able to do the calculations. In algebraic expressions, you will frequently use the formulas explained earlier.

In algebraic expressions, there are many situations where you have to develop the equation, as shown below. How do we solve such equations?

  • $2(3x-4y)$
  • $3a(a+3)$

The distributive property holds not only for numbers but also for letters. So when we expand the equation, we can multiply all the equations in parentheses like below.

If there are equations with pluses or minuses in parentheses, multiply each of them.

Multiply All Numbers in Parentheses by Minus or Fractions

However, when calculating using the distributive law, calculation errors often occur. In polynomial multiplication and division, miscalculations are more likely to occur in the following.

  • Negative multiplication
  • Multiplying fractions

In the distributive property, all the equations in the parentheses are multiplied. So, if you want to multiply minus sign by the distributive property, you must multiply all the equations in the parentheses by the minus sign. This means that all the signs will change.

When expanding an equation, it is wrong to change the sign of only one of the equations in parentheses. For example, the following calculation is wrong.

  • $−2(3x+1)=-6x\textcolor{red}{+}2$

The same can be said for fractions. In multiplying fractions, if a negative sign is in front of a fraction, you must do the following.

  • $-\displaystyle\frac{2x-3}{4}=\displaystyle\frac{-2x+3}{4}$

$-\displaystyle\frac{2x-3}{4}$ has the same meaning as $\displaystyle\frac{-(2x-3)}{4}$. So when you remove the parentheses, make sure the signs are correct.

Divisions Are Converted to Multiplying Fractions and Perform Reduction

Note that in math calculations, we don’t use division in all equations after we learn the algebraic expressions. By using the reciprocal, we can always convert them into multiplying fractions. Just be sure to pay attention to the position of the numerator and denominator when using reciprocals.

For example, $\displaystyle\frac{2}{3}x=\displaystyle\frac{2x}{3}$. Therefore, the reciprocal of $\displaystyle\frac{2}{3}x$ is $\displaystyle\frac{3}{2x}$. When making the reciprocal of $\displaystyle\frac{2}{3}x$, it must not be $\displaystyle\frac{3}{2}x$.

So, for example, the calculation would look like this.

When multiplying (or dividing) in an algebraic expression, there are multiple points where calculation errors can occur. You need to understand which parts of the equation are most likely to be miscalculated and make sure that the signs and reciprocals are correct.

Putting Numbers into Algebraic Expressions by Substitution

Why do we need to learn how to calculate polynomials? Because it can be converted into simple calculations.

The reason why we need to learn math is that it is used frequently in our daily lives. Mathematics is used for calculations not only in science but also in bookkeeping, programming, marketing, and all other situations. This is why we create an alphabetic equation and put in numbers to get the answer.

For example, we have the following equation.

  • $3x+1$

The answer to this equation depends on what numbers you apply to it, as follows.

Applying a number to an algebraic expression is called substitution. By substituting, you will be able to get the answer you are looking for.

Calculating Polynomials to Simplify Equations

By using substitutions, we can get a specific answer. For example, if $x=3$, the substitution gives the following.

  • $2x-2=2×3-2=4$
  • $x^2=3×3=9$

If the algebraic expressions are simple, the problem can be solved without any difficulty. On the other hand, if $x=-3,y=2$, what will be the answer if we substitute into the following equation?

  • $-3(3x-5y)+4(8x-4y)$

You can calculate by substituting numbers into this equation. However, the calculation is so complicated.

  • $-3[3×(-3)-5×2]+4[8×(-3)-4×2]$

So in the algebraic expressions, we calculate the algebraic expressions first. Therefore, we have the following.

Calculating the algebraic expression yields $23x-y$. After simplifying the algebraic expression by addition, subtraction, multiplication, and division, it is easy to calculate when substituting. If $x=-3,y=2$, we have the following.

$23x-y$.

$=23×(-3)-2$

$=-69-2=-71$

When you substitute, calculate the algebraic expressions first. Then, substitute numbers into the alphabet to get the answer.

Exercises: Polynomial Calculations and Substitutions

Q1: Do the following calculation.

  1. $3(4x+3)-4(2x-1)$
  2. $\displaystyle\frac{2x+3}{2}-\displaystyle\frac{x+4}{3}$

A1: Answers.

In polynomial multiplication, you have to be careful when removing the parentheses. If there is a minus sign before the parentheses, all the signs change when the parentheses are removed.

The same is true for fractions. If a minus sign is present in front of a fraction, the sign will change according to the distributive property. So we get the following calculation.

(a)

$3(4x+3)-4(2x-1)$

$=12x+9-8x+4$

$=4x+13$

(b)

Q2: if $x=3$ and $y=-2$, do the following calculation.

  1. $-3(2x+2y)+2(4x-5y)$
  2. $(2x^2+4xy)÷\displaystyle\frac{2}{3}x$

A2: Answers.

In the substitution calculations, calculate the algebraic expressions first. If you do so, it will be easier to calculate when you substitute numbers.

(a)

$-3(2x+2y)+2(4x-5y)$

$=-6x-6y+8x-10y$

$=2x-16y$

  • Substitute $x=3,y=-2$.

$2x-16y$

$=2×3-16×(-2)$

$=6+32=38$

(b)

$(2x^2+4xy)÷\displaystyle\frac{2}{3}x$ : Move $x$ to the numerator

$=(2x^2+4xy)÷\displaystyle\frac{2x}{3}$ : Convert to multiplication

$=(2x^2+4xy)×\displaystyle\frac{3}{2x}$ : Distributive law

$=2x^2×\displaystyle\frac{3}{2x}+4xy×\displaystyle\frac{3}{2x}$ :Reduce

$=3x+6y$

  • Substitute $x=3,y=-2$.

$3x+6y$

$=3×3+6×(-2)$

$=9-12=-3$

Learn How to Calculate Distributive Property and Polynomials

In mathematics, calculations are almost always done with algebraic expressions. Therefore, you need to understand how to calculate polynomials. After learning addition and subtraction, the next important thing to learn is how to multiply and divide polynomials.

In order to multiply (or divide) polynomials, you must learn the distributive property. We have explained why distributive law is established. Be sure to understand the principles of distributive property.

In addition, there are some points where many people make calculation errors when calculating algebraic expressions using the distributive law. The following are the parts.

  • The minus exists in front of the parenthesis.
  • The minus exists in front of the fraction.
  • Use reciprocals to convert division into multiplying fractions.

If there is a minus sign in front of the parentheses or fraction, be careful whether the sign is positive or negative when you expand the expression using the distributive law. Also, when using reciprocals, check whether the letters are in the numerator or denominator. If you pay attention to these, you will be able to avoid mistakes in your calculations.