In mathematics, we learn algebraic expressions using the alphabet. We use symbols to perform calculations such as addition, subtraction, multiplication, and division.
Parentheses are often used in math calculations. When multiplying parentheses by parentheses, we use factoring formulas.
Once you learn factoring formulas, you will also be able to factorize them. Factorization is the way to convert polynomials into multiplication equations using parentheses. In calculating polynomials, factorization is more difficult than expanding an expression using factoring formulas, so you need to understand how to calculate it.
Learning factoring formula and factorization together will make the math easier to understand. We will explain how to use the factoring formula and solve factorization problems.
Table of Contents
Proof of Multiplication of Polynomials by the Distributive Property
In polynomial calculations, there are so many problems that require us to expand equations. Removing the parentheses so that the equation takes the form of addition and subtraction of monomials is called expanding (or developing). In expanding equations, multiplying two parentheses can be complicated.
Specifically, we do the following calculation.
- $(a+b)(c+d)$
In other words, multiply $(a+b)$ by $(c+d)$. How do we do this kind of polynomial calculation?
When multiplying two polynomials, expand the expression as follows.
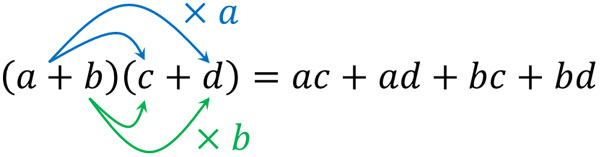
Why is it possible to develop an equation in this way? In mathematics, we need to understand why. So, let’s try to prove that this formula is valid.
As we know from learning algebraic expressions, numbers can be replaced with letters. So let’s replace $(c+d)$ with $N$. Then $(a+b)(c+d)$ becomes $(a+b)N$. Therefore, by using the distributive property (or distributive law), we can calculate the following.
- $(a+b)N=aN+bN$
$N$ is $(c+d)$. So, we substitute $N=(c+d)$. The result is the following calculation.
$aN+bN$
$=a(c+d)+b(c+d)$
$=ac+ad+bc+bd$
From this result, we can prove that $(a+b)(c+d)=ac+ad+bc+bd$ holds. In the multiplication of two polynomials, we can use this formula to expand the equation.
However, we don’t have to prove the above formula every time when we do math calculations. So understand that this formula holds and remember how to calculate it. Learn how to expand the equation.
Expanding the Equation Using the Four Factoring Formulas
By using the formula we just discussed, we can understand that the factoring formulas are established. Factoring formulas are formulas that are used to expand or factor.
There are four important factoring formulas. Each of them is as follows.
- $(x+a)(x+b)=x^2+(a+b)x+ab$
- $(x+a)^2=x^2+2ax+a^2$
- $(x-a)^2=x^2-2ax+a^2$
- $(x+a)(x-a)=x^2-a^2$
You must remember all four of these factoring formulas. If you don’t, you won’t be able to calculate polynomials efficiently.
It is easy to prove why these formulas are valid. Using the formulae discussed previously, we can create factoring formulas. We will check each of them.
-Factoring Formula: Part 1
$(x+a)(x+b)$ can be calculated as follows.

By expanding the equation, we can see that $(x+a)(x+b)=x^2+(a+b)x+ab$. This is the most frequently used factoring formula in mathematics and must be memorized.
For example, when solving the problem $(x+1)(x+2)$, we can use the factoring formula to expand the equation as follows.
$(x+1)(x+3)$
$=x^2+(1+3)x+1×3$
$=x^2+4x+3$
-Factoring Formula: Part 2
In the same way, we can get the factoring formula by expanding the polynomial. $(x+a)^2$ is as follows.
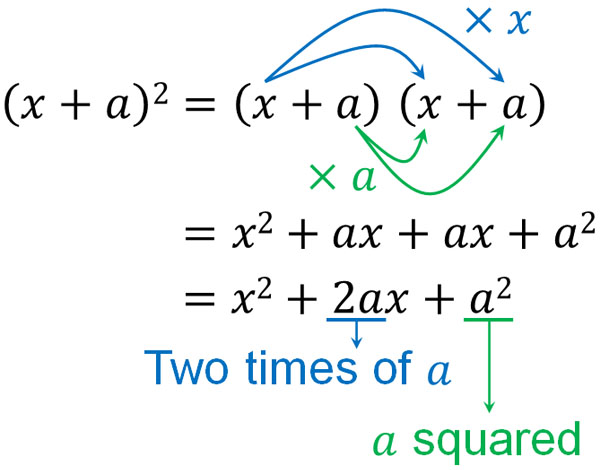
In the previous factoring formula, the numbers of $a$ and $b$ are different. This factoring formula, on the other hand, squares $(x+a)$. So the answer is $2ax$ instead of $(a+b)x$. Also, it is $a^2$, not $ab$.
-Factoring Formula: Part 3
In contrast, $(x-a)^2$ is as follows.
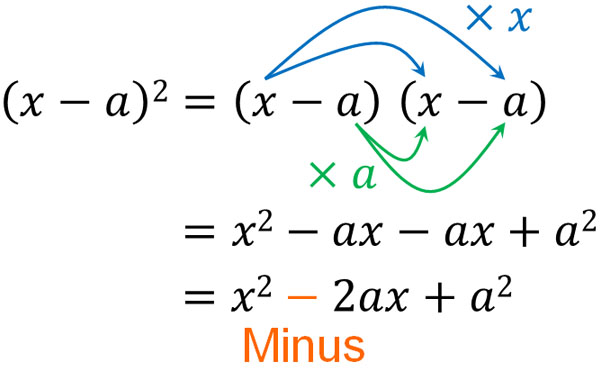
In contrast to $(x+a)^2$, the sign is negative in $(x-a)^2$. Although it is just a plus sign becoming a minus sign, it is important in factoring formulas. Note that $(x+a)^2$ has $a^2$ in the same way.
-Factoring Formula: Part 4
The factoring formula for $(x+a)(x-a)$ can be calculated as follows.
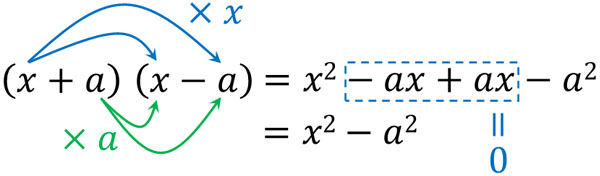
$-ax+ax=0$. Therefore, calculating $(x+a)(x-a)$ gives us $x^2-a^2$.
Compared to other factoring formulas, $(x+a)(x-a)=x^2-a^2$ is used less often. However, you must remember it as a factoring formula.
If You Forget the Factoring Formulas, You Can Still Calculate
In some cases, you may forget the four factoring formulas. Even in that case, there is no problem. You just need to calculate $(a+b)(c+d)=ac+ad+bc+bd$.
For example, let’s say you want to calculate $(x-3)^2$. Using the factoring formulas mentioned earlier, you can quickly get the answer to $x^2-6x+9$. But even if you forget the factoring formulas, you can still expand the equation by multiplying each of them. It is as follows.
$(x-3)^2$
$=(x-3)(x-3)$
$=x^2-3x-3x+9$
$=x^2-6x+9$
If you remember the factoring formulas, you can skip these calculations and get the answer. However, even if you forget, you can still do the math to get the answer.
Factorization: Making Parentheses Equations
After learning about expanding expressions in math, the next step to study is factorization. Expanding an expression is to remove the parentheses. On the other hand, what is factorization? Factorization is the opposite of expansion of an equation. In other words, you create an expression with parentheses from an expression without parentheses.
The multiplication equation is called a factor. For an equation that is made up of addition and subtraction, we decompose it so that it becomes a multiplication of factors.
In factorization, we need to find common factors. For example, we get the following.
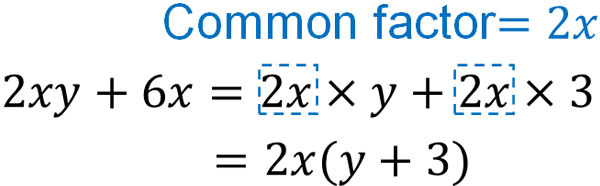
Factoring is more difficult than expanding expressions. In expression expansion, it is clear which numbers need to be multiplied. In factoring, on the other hand, you need to look for common factors. Since the common factors are not written down, you have to find out which ones are the common factors.
Factorization Has Multiple Options
Also, in the case of factorization, many questions are based on the factoring formulas. In other words, if you forget the factoring formulas, you will not be able to solve them. In equation expansion, even if you forget the factoring formulas, you can still get the answer. On the other hand, factorization requires you to remember the factoring formulas.
In factorization using the factoring formulas, there are multiple choices. You have to find the best answer out of them.
For example, how can we factor the following expression?
- $x^2+4x+3$
As we explained earlier, there are four factoring formulas. In other words, you have to choose the best factoring formula among the four options. Among the factoring formulas, the following formula is the most frequently used in factorization.
- $(x+a)(x+b)=x^2+(a+b)x+ab$
Comparing $x^2+4x+3$ and $x^2+(a+b)x+ab$, we can get the following.
- $a+b=4$
- $ab=3$
We have to find factors that satisfy these two. Note that there is the best way of factorization. That is, we need to focus on multiplication.
-Addition and Subtraction Have Infinite Answers
If we apply $a$ and $b$ so that $a+b=4$, there are infinitely many answers. For example, we have the following.
- $2+2=4$
- $10-6=4$
- $-100+104=4$
So when we factorize, we don’t focus on $a+b$ first. Instead, we focus on $ab$, which is multiplication. There are only two integers that satisfy $ab=3$ as follows.
- $1×3=3$
- $-1×(-3)=3$
In other words, there are two candidates for the answer when factoring. Which one is the correct answer? So, we need to find the number that satisfies $a+b=4$. The result is as follows.
- If $a=1,b=3$, then $1+3=4$
- If $a=-1,b=-3$, then $-1+(-3)=-4$
If $a=1,b=3$, then both $a+b=4$ and $ab=3$ are satisfied. Therefore, we can factorize it as follows.
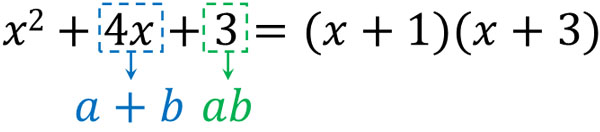
Thus, in factorization, we have to figure out the correct answer from multiple candidates. In this example, we used the factorization of a simple equation as an example. However, if the expression is more complicated, factoring becomes more difficult.
Factorization Using the Four-Pattern Formula
As mentioned above, there are four factoring formulas. Therefore, when you are learning factorization for the first time, you have to choose which of the four factoring formulas to use. Although there are other formulas for factorization, those should be learned when learning more challenging math, such as high school.
One way to distinguish the factoring formulas used in factoring is to check if they contain powers. Of the four factoring formulas, the following three include powers.
- $(x+a)^2=x^2+2ax+\textcolor{red}{a^2}$
- $(x-a)^2=x^2-2ax+\textcolor{red}{a^2}$
- $(x+a)(x-a)=x^2-\textcolor{red}{a^2}$
If powers are included, these factoring formulas may be used to factorize them. For example, how can we factor the following polynomial?
- $x^2+6x+9$
- $x^2-6x+9$
$3^2=9$. So we can see that these polynomials contain powers. Also, if we double 3, we get 6. Therefore, we can factorize them as follows.

If it can be powered, and further doubling the number yields $2ax$ (or $-2ax$), it can be factored using the factoring formula.
On the other hand, how can we factor the following case?
- $x^2-25$
$5^2=25$, and this equation contains a power. It also has a negative sign and the $2ax$ or $(a+b)x$ does not exist. If these conditions are met, the following factorization is possible.
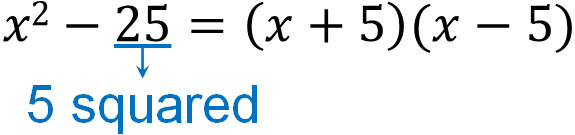
In this way, we can factorize using the factoring formulas.
-Factorization When There Is No Power
There are often cases where the three factoring formulas explained earlier cannot be used, such as not including a power in the equation. In such cases, the following factoring formula can be used to factorize the equation.
- $(x+a)(x+b)=x^2+(a+b)x+ab$
We have already discussed how to factorize using this factoring formula. We will use this factoring formula most often in factorization. In any case, you should be able to find the answer from multiple choices in factoring.
Exercises: Factoring Formulas and Factorization Calculations
Q1: Expand the following equation.
- $(x-3)(x+5)$
- $(x+4)^2-(2x+3)(x-6)$
A1: Answers.
The factoring formulas can be used to develop the equations.
(a)
$(x-3)(x+5)=x^2+2x-15$
(b)
$(x+4)^2-(2x+3)(x-6)$
$=x^2+8x+16-(2x^2-12x+3x-18)$
$=x^2+8x+16-2x^2+12x-3x+18$
$=-x^2+17x+34$
Q2: Factorize the following equation.
- $x^2-6x-16$
- $x^2y-49y$
- $(2x+3)(2x-3)-5x(x-2)$
A2: Answers.
You can factor the equation by using the factoring formulas. You may also factor the equation after expanding it.
(a)
In factorization, we first focus on multiplication. So let’s check the -16 in $x^2-6x\textcolor{red}{-16}$. Here are some candidates for the numbers that become -16 in multiplication.
- $1×(-16)=-16$
- $-1×16=-16$
- $2×(-8)=-16$
- $-2×8=-16$
- $4×(-4)=-16$
Among these candidates, which number satisfies $a+b=-6$? If $a=2,b=-8$, then $a+b=-6$. Therefore, we can factorize it as follows.
- $x^2-6x-16=(x+2)(x-8)$
(b)
In factorization, we don’t always use the factoring formulas first. In some cases, the factoring formula is used after the common factors are put together.
In $x^2\textcolor{red}{y}-49\textcolor{red}{y}$, $y$ is the common factor. So the first factorization is as follows.
- $x^2y-49y=y(x^2-49)$
It is important to note that $(x^2-49)$ can be further factored. Therefore, we can factor it as follows.
- $y(x^2-49)=y(x+7)(x-7)$
(c)
Sometimes, after expanding an expression, we need to factor it. So, do the following calculations first.
$\textcolor{red}{(2x+3)(2x-3)}-5x(x-2)$
$=\textcolor{red}{4x^2-9}-5x^2+10x$
$=-x^2+10x-9$
After expanding the equation in this way, we factor it. The factorization of this equation is as follows.
$-x^2+10x-9$
$=-(x^2-10x+9)$
$=-(x-1)(x-9)$
Q3: Factorize the following equation.
- $(x+2)(x-2)+y(2x+y)$
A3: Answers.
First, we need to expand the equation. Therefore, we have the following.
$(x+2)(x-2)+y(2x+y)$
$=x^2-4+2xy+y^2$
$=x^2+2xy+y^2-4$
After this, how can we factorize it? In this equation, we can separate it into two parts as follows.
- $\textcolor{red}{x^2+2xy+y^2}-4$
If we focus on $x^2+2xy+y^2$, we can factorize it as follows.
$\textcolor{red}{x^2+2xy+y^2}-4$
$=(x+y)^2-4$
However, it is not yet an expression of multiplication only. In other words, we need to factor it further. So if we check the equation, we can notice that $4=2^2$.
Also, $(x+y)$ is hard to understand, so let’s replace it with $(x+y)=N$. Then we get the following.
- $\textcolor{red}{(x+y)}^2-4=\textcolor{red}{N}^2-2^2$
By substituting the equation in this way, notice that we can factorize it using the factoring formula. We can factor it as follows.
- $N^2–2^2=(N+2)(N-2)$
However, $N=x+y$. Then, by substituting $N=x+y$, we can complete the factorization as follows.
- $(N+2)(N-2)=(x+y+2)(x+y-2)$
Use Factoring Formulas and Factorization to Solve Polynomial Problems
In mathematics, factoring formulas and factorization should be understood as a set. So you need to be able to factor as well as develop equations using the factoring formulas.
The factoring formulas must be memorized; you have to be able to use the four factoring formulas. In equation development, you don’t need to memorize the factoring formulas to get the answer. On the other hand, in factorization, you have to remember the factoring formulas to get the answer.
Compared to equation expansion using the factoring formulas, factorization has many more candidate numbers and is more difficult to answer. However, in the sense of using the factoring formulas, both equation expansion and factorization are the same.
One of the most important contents in mathematics is equation expansion and factorization using factoring formulas. Try to understand how to use factoring formulas to expand and factor expressions.