In elementary geometry, we learn about quadrilaterals and triangles. We are often asked to find the area of a shape. The area is the size of the shape, and you can find the area of a quadrilateral or triangle by using the formula. On the other hand, if you don’t remember the formula, you won’t be able to calculate the area.
However, there are different types of quadrilaterals. For example, the formula to find the area of a rectangle is different from the formula to find the area of a trapezoid. Therefore, you need to learn the formula for each.
You also need to understand why the formula is valid. In math, learning the reason is important, not just remembering the formula and calculating it.
So, we will explain how to calculate the area of quadrilaterals and triangles. We will also explain why the formulas are valid.
Table of Contents
Formulas for Calculating the Area of Squares and Rectangles
In geometry problems, there are many questions that ask for the area. So, it is important to understand how to calculate the area of a shape (the size of the shape). It is easier to calculate the area of a quadrilateral than a triangle. So let’s look at how to calculate the area of a quadrilateral first.
Squares and rectangles are the most common shapes among quadrilaterals. The formula for calculating the area of a square or rectangle is as follows.
- Area = Length × Width
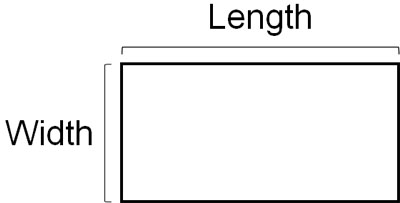
In other words, you can find the area of a square or rectangle if you know its vertical and horizontal lengths. For example, what is the area of the following square and rectangle?
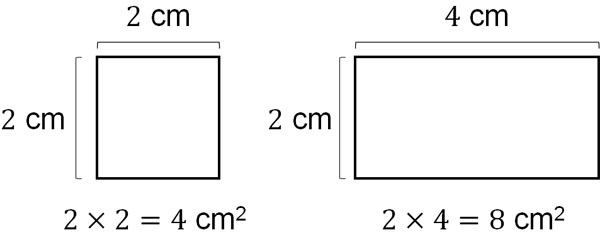
The length of a square is 2 cm, and the width is 2 cm. Therefore, the area is $2×2=4$ cm2. The rectangle is 2 cm in width and 4 cm in length. Therefore, the area is $2×4=8$ cm2. Note that the number 2 is used as the unit of area; cm2 (square centimeter), m2 (square meter), and km2 (square kilometer) are the units of area.
Why Is the Formula for Area Valid?
Why is it possible to find the area by multiplying the vertical length by the horizontal length? Let’s try to understand why the formula for area is valid.
How many square centimeters is the area of 1 cm long and 1 cm wide? The answer is 1 cm2.
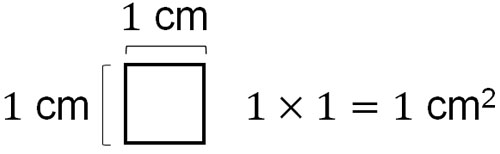
So, let’s count how many 1 cm2 there are. For example, in a square 2 cm long and 2 cm wide, there are $2×2=4$ squares of 1 cm2. Also, in a rectangle of 2 cm in length and 4 cm in width, there are $2×4=8$ squares of 1 cm2.
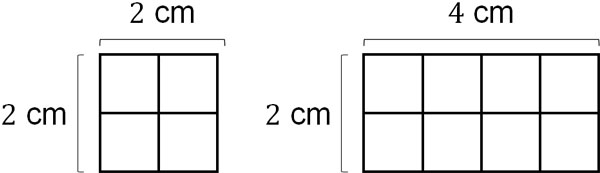
If we consider how many 1 cm2 there are, we can see why the formula for area is valid. If we count the 1 cm2 one by one, we will get the area. However, this method takes a lot of time, so we need to multiply the vertical length by the horizontal length.
The Method for Finding the Area of a Parallelogram Is the Same
How do we calculate the area of the other quadrilaterals? For parallelograms, the area calculation method is the same as the previous one. Use the following formula.
- Area = Base × Height
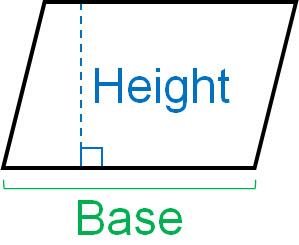
Just like a square and a rectangle, you can multiply the length (base) and the width (height) to get the area. The reason is that the area of a parallelogram can be changed into the area of a square or rectangle. For example, if you change the shape of the following parallelogram, it becomes a square.
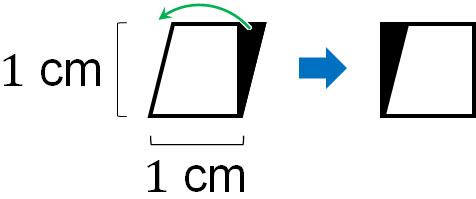
The area represents the size of a shape. Since parallelograms and squares (or rectangles) have the same area, the formula for finding the area of a parallelogram is the same as the formula for finding the area of a square or rectangle.
Calculating the Area of a Trapezoid Using the Upper and Lower Bases
On the other hand, how do you calculate the area of a trapezoid? Among the quadrilaterals, we use a special formula for the trapezoid. Here is the formula to find the area of a trapezoid.
- Area of a trapezoid = (Base1 + Base2) × Height ÷ 2
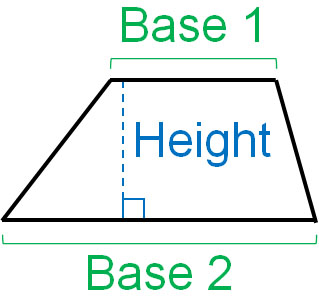
Why do we add the upper and lower bases in the formula for finding the area of a trapezoid? The reason is that by using two of the same trapezoid, we can make a parallelogram.
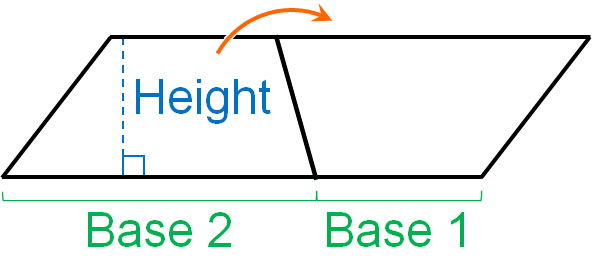
If we add the upper and lower bases, we get the horizontal length of the parallelogram. Then, if we multiply the horizontal by the vertical, we can get the area of the parallelogram. However, the area of a parallelogram is calculated by using two trapezoids of the same shape. So, after finding the area of the parallelogram, we need to divide by 2 to get the area of the trapezoid.
Using Diagonals to Calculate the Area of a Rhombus
Some quadrilaterals are rhombuses. To find the area of a rhombus, you can use a special formula.
- Area of a rhombus = diagonal × diagonal ÷ 2
Note that if the diagonals intersect perpendicularly, you can use this formula for all quadrilaterals. So even if all the sides are not equal in length, you can use this formula to find the area (right side of the figure below). Specifically, you can use the formula in the following quadrilaterals (the left side of the figure below is a rhombus)

Why is this formula valid? The diagonals of a rhombus can be considered as the vertical and horizontal lengths of a rectangle, as shown below.
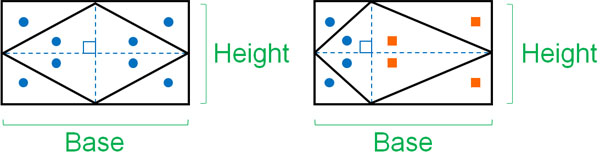
*The left figure: a rhombus, the right figure: a quadrilateral with perpendicular intersecting diagonals.
In other words, multiplying a diagonal by a diagonal is the same as multiplying a vertical by a horizontal to get the area of a rectangle. Also, it is important to note that each ● is the same shape. And each ■ is the same shape. Therefore, if you find the area of a rectangle and then halve it, you will find the area of a rhombus.
Using the Base and Height to Find the Area of a Triangle
Next, let’s understand the formula for finding the area of a triangle. The formula for finding the area of a triangle is as follows.
- Area of a triangle = Base × Height ÷ 2

When calculating the area of a triangle, try to figure out where the base is and where the height is. The height is the line perpendicular to the base, so make sure that the two lines are at right angles.
Why Is the Formula for the Area of a Triangle Valid?
Next, we will explain why the formula for the area of a triangle is valid. Why do we divide by 2 to get the area of a triangle?
If we multiply the base by the height, we can get the area of a parallelogram. We can create a parallelogram by using two triangles of the same shape, as shown below.
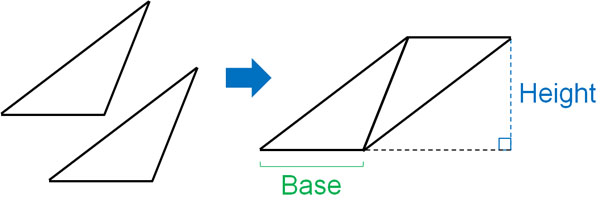
However, what we want to know is not the area of a parallelogram but the area of a triangle. In the area of a parallelogram, we are using two triangles of the same shape. So, let’s cut the area of the parallelogram in half. Then we can get the area of the triangle.
Using Formulas for Quadrilaterals and Triangles to Find Area
Use formulas to find the area of shapes. The easiest formulas for finding area are for squares and rectangles. By multiplying the vertical length by the horizontal length, you can find the area of a square or rectangle. The area of a parallelogram can also be obtained by multiplying the base by the height.
However, to find the area of a trapezoid, you will need to use a special formula. If you don’t remember the formula, you won’t be able to get the area of a trapezoid. Therefore, be sure to memorize it. Also, you can use diagonals to calculate the area of a rhombus.
Once you understand the formula to find the area of a quadrilateral, it will be easier to remember the formula to find the area of a triangle. For triangles, multiply the base by the height, and then divide by 2 to get the area.
Use the formula to find the area of a shape. Also, if you understand why the formula is valid, it will help you in your math calculations.