In elementary math, we learn about shapes. An important part of shapes is an angle, and the shape changes depending on the angle.
Among the angles, a special angle is a right angle. If the angle is 90 degrees, it is called a right angle. After learning about right angles, we also need to learn about perpendicular lines and parallel lines.
By learning about right angles, perpendicular lines, and parallel lines, you will be able to understand shapes. Also, by using perpendicular lines and parallel lines, you will be able to know the area of a shape. In this section, we will explain the concept of right angle, perpendicular, and parallel.
Table of Contents
Angles Are Important in Plane Figures
When two lines intersect, the size of the intersecting lines is called the angle. The following is an angle.
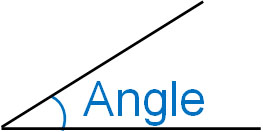
The size of the angle is determined by the intersection of the two lines. For a full revolution, the angle is 360°. In the case of a straight line, the angle is 180°. This is the rule.

After understanding the properties of angles, let’s review the concepts of right angles, perpendicular lines, and parallel lines.
A Right Angle Has an Angle of 90°
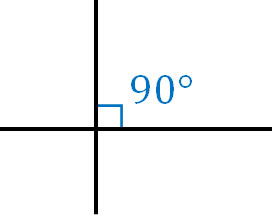
When an angle is 90°, that angle is called a right angle. The following angle is a right angle.
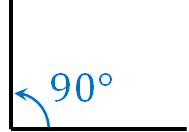
If there are two 90° angles, it becomes a straight line. As mentioned earlier, the angle of a straight line is 180°. If there are four 90° angles, the angle is 360°. The angle of one rotation is 360°.
In the Perpendicular, the Two Lines Intersect at Right Angle
Also similar to a right angle is a perpendicular. A right angle means that the angle is 90°. A right angle is equal to 90°. On the other hand, when two lines intersect, if the angle is 90°, then the two lines are perpendicular.
Perpendicular is a term that describes the relationship between two lines.
If the angle is not 90°, the two lines are not perpendicular. For lines that intersect at right angles and lines that do not intersect at right angles, think of them as follows
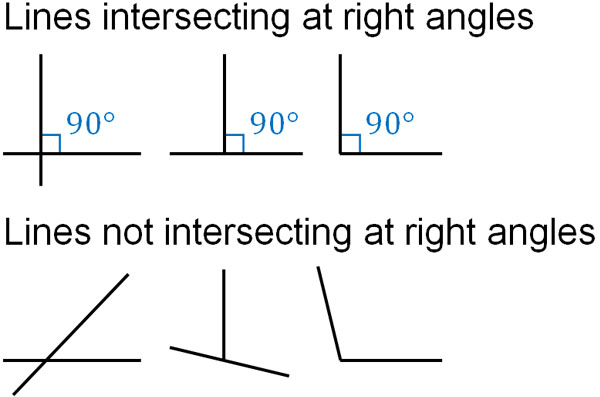
You can determine if two lines intersect at a right angle by checking if they intersect at 90°.
Two Lines Perpendicular to a Line Are Parallel Lines
In addition, we also learn the term parallel in shapes. Parallel lines refer to two lines that are perpendicular to a line. The following two blue lines are parallel to each other.
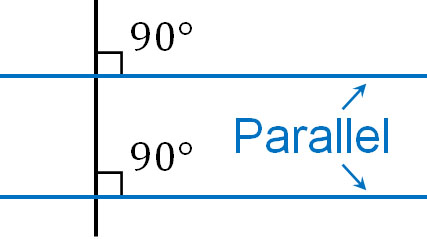
A simpler way to describe parallel lines is lines that never intersect. If two lines are parallel, they will never intersect no matter how far you extend the lines.
Since parallel lines are lines that do not intersect when two lines are extended in a straight line, we can determine whether two lines are parallel or not as follows.

If the two lines do not intersect when extended, they are parallel.
Use Triangular Rulers to Make Perpendicular Lines and Parallel Lines
Next, let’s learn how to draw perpendicular and parallel lines. In elementary school math, we use triangle rulers to make perpendicular and parallel lines.
A triangle ruler includes a triangle with a right angle. So after making a horizontal line using a triangle ruler, let’s make a right angle using a triangle ruler, as shown below.
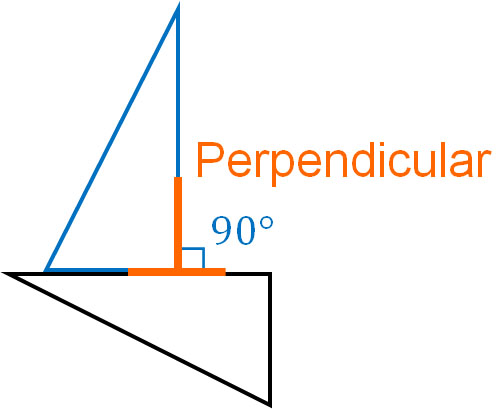
On the other hand, how do you draw parallel lines? First, align the line and the triangle ruler. After that, make a perpendicular with the other triangle ruler. Then, slide the ruler up or down. It will look like this.
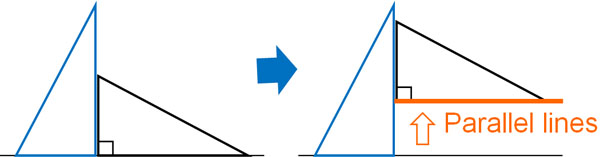
In any case, by using two triangular rulers, you can draw perpendicular and parallel lines.
Vertical and Horizontal Lines Have a Perpendicular Relationship
When learning about geometry, it is important to understand angles. In particular, perpendicular lines and parallel lines are often used in geometry problems. For example, you can calculate the area of a triangle if you know the vertical and horizontal lengths.
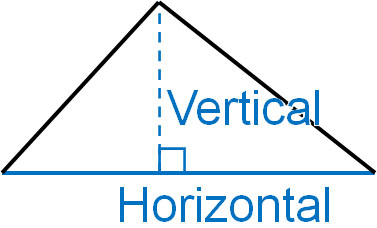
A vertical length is a line that is perpendicular to a horizontal line. If it is not perpendicular to the horizontal line, it is not a vertical line. In other words, if you don’t understand right angles and perpendicular lines, you can’t calculate the area of a shape.
Also, you can calculate the area of a rectangle if you know its vertical and horizontal lengths, just like a triangle.
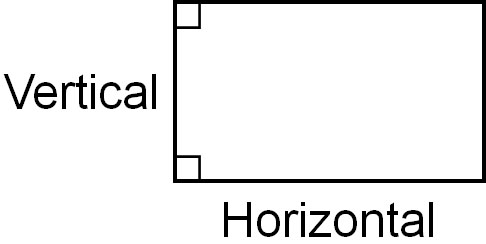
You cannot calculate the area of a rectangle if the horizontal lines are not parallel. Therefore, in order to do the calculation, it must be a quadrilateral with perpendicular and parallel lines.
Right Angles, Perpendicular Lines, and Parallel Lines Are Familiar
A right angle is a special angle. So why do we use perpendicular lines and parallel lines so often in shapes, even though right angles are special angles? The reason is that we are surrounded by a lot of perpendicular lines and parallel lines. For example, in a house, the wall is perpendicular to the floor.

Also, what is the relationship between the floor and the ceiling? In many cases, the floor and ceiling are parallel. Because the walls are perpendicular to the floor and the ceiling, they are parallel to each other.
Although 90 degrees is a special angle, we are surrounded by many right angles. This is why problems involving perpendicular and parallel shapes are often asked.
Right Angles, Perpendicular Liens, and Parallel Lines Are Important in Angles
We first learn about angles in shapes. After learning the concept of angles, the next thing you will learn is right angles. A right angle is the most commonly used angle. It is important to understand that a right angle is 90 degrees.
After learning about right angles, we also need to learn about perpendicular and parallel lines. If two lines intersect at 90°, they are perpendicular lines. Also, if two lines are straight and do not intersect, they are parallel lines.
When we look around us, there are many shapes that are perpendicular or parallel. The angle is often 90 degrees, and there are many right angles in plane figure problems. So try to understand the relationship between right angles, perpendicular lines, and parallel lines.