Fractions are used frequently in our daily lives. So if you don’t understand the concept of fractions, you won’t be able to do calculations in your daily life.
Fractions can be used to express numbers smaller than one, and they are used to divide things into multiple parts. There are many situations where fractions are used, such as when dividing things or shopping.
There are different types of fractions: proper fractions, improper fractions, and mixed fractions. We do not use mixed fractions in junior high school and high school mathematics. However, when learning about fractions, you need to understand the basics. So, let’s learn about all types of fractions first.
Also, in fractions, you have to learn the numerator and denominator. So let’s learn about the types and properties of fractions.
Table of Contents
What Is a Fraction: A Number Less Than 1
First of all, what is a fraction? Fractions are a way of expressing numbers that are less than one. Decimals are a way to express numbers less than one. Not only decimals, but also fractions can express numbers smaller than one.
Why do we learn fractions? Because fractions are useful. For example, if you want to divide a cake into five pieces, how do you express it?

In this case, we use fractions, because we are dividing a cake into five pieces, which is a number smaller than one. When dealing with small numbers, we use fractions. Numbers such as the following are fractions.
- $\displaystyle\frac{2}{3}$, $\displaystyle\frac{1}{10}$, $\displaystyle\frac{3}{8}$
There are many situations where we use fractions in math.
The Concept of Numerator and Denominator
How do we use fractions? Fractions have a numerator and a denominator. Let’s try to remember what these terms mean. The number in the upper part of the fraction is called the numerator. The number in the lower part of the fraction is called the denominator. It looks like this.

The denominator indicates how many parts a thing is divided into. For example, if a cake is divided into three parts, the denominator will be three, and if it is divided into five parts, the denominator will be five.
The denominator is determined by how many equal parts you divide it into, as shown below.
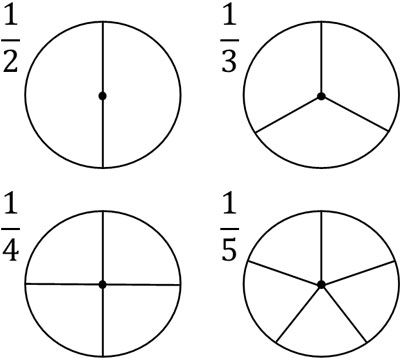
On the other hand, what does the numerator mean? As I mentioned before, the denominator is the number after dividing. The numerator, on the other hand, is the number of pieces that remain after the division.
For example, if you divide a cake into 5 pieces and you can eat 2 of them, the number of pieces you can eat is $\displaystyle\frac{2}{5}$. On the other hand, if the cake is divided into 5 pieces and you can eat 3 pieces, the number of cakes you can eat is $\displaystyle\frac{3}{5}$.
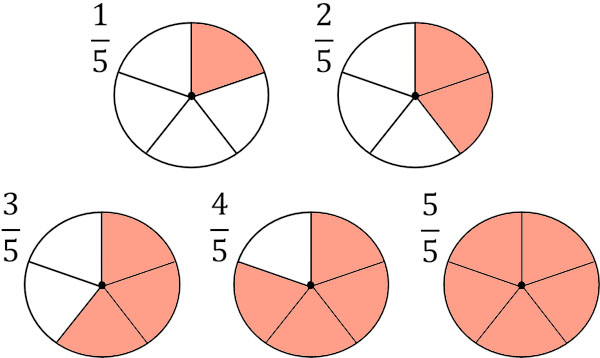
The numerator is the number of pieces after dividing the number. Fractions always have a numerator and a denominator.
The Relationship Between Division and Fractions
So what do fractions represent? Fractions have the same meaning as division. For example, $\displaystyle\frac{1}{4}$ means that 1 is divided into 4 equal parts. In other words, it is the same as $1÷4$. Also, $\displaystyle\frac{3}{5}$ means that 3 is divided into 5 equal parts. Therefore, $\displaystyle\frac{3}{5}$ is the same as $3÷5$.
So, the relationship between division and fractions is as follows, for example.
- $4÷9=\displaystyle\frac{4}{9}$
- $13÷2=\displaystyle\frac{13}{2}$
- $1÷3=\displaystyle\frac{1}{3}$
- $5÷6=\displaystyle\frac{5}{6}$
Divisors can be converted to fractions. Fractions can also be converted to divisions. When converting a division to a fraction, the dividend will be the numerator and the divisor will be the denominator.
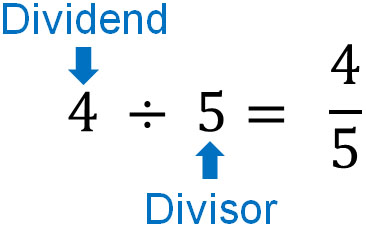
The relationship between division and fractions is important in arithmetic calculations. There are many situations where you need to convert a division into a fraction, so make sure you understand how.
The Difference Between Proper Fractions, Improper Fractions, and Mixed Fractions
There are some types of fractions. In elementary school math, we learn the following fractions.
- Proper fractions: Fractions where the numerator is smaller than the denominator.
- Improper fractions: Fractions where the numerator and denominator are the same or where the numerator is larger than the denominator.
- Mixed fractions: Fractions that combine integers and proper fractions.
For example, the following.

In advanced calculations, such as middle school and high school mathematics, we do not use mixed fractions. Usually, only proper and improper fractions are used. However, there are these types of fractions, and you should try to learn all of them first.
Converting an Improper Fraction to an Integer
Next, let’s convert an improper fraction into an integer. How can we change the form of an improper fraction?
As mentioned above, fractions can be turned into division expressions. So if you want to turn a fraction into an integer, you can convert it into a division expression. For example, it would look like this.
- $\displaystyle\frac{6}{2}=6÷2=3$
- $\displaystyle\frac{20}{5}=20÷5=4$
In this way, we can convert an improper fraction to an integer. On the other hand, how do we calculate the fraction if it is not divisible? For example, what is the integer in $\displaystyle\frac{14}{3}$? In this case, let’s use the remainder to get the answer. The answer is as follows.
- $\displaystyle\frac{14}{3}=14÷3=4$ R 2
As you can see, by using the remainder, we can turn a fraction into an integer.
Converting an Improper Fraction to a Mixed Fraction
Next, let’s convert an improper fraction into a mixed fraction. A mixed fraction is a fraction that is a mixture of an integer and a proper fraction. The integer is written on the left, and the proper fraction is written on the right. We can also think of mixed fractions as adding, as follows.
- $1\displaystyle\frac{2}{3}=1+\displaystyle\frac{2}{3}$
- $3\displaystyle\frac{3}{7}=3+\displaystyle\frac{3}{7}$
In a mixed fraction, we omit the + sign. For example, $1\displaystyle\frac{2}{3}$ would look like the following.
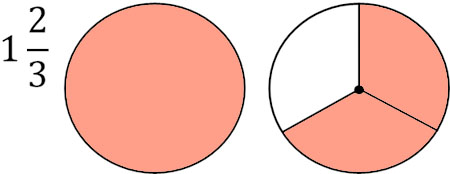
Also, as mentioned earlier, in an improper fraction, the number in the numerator is larger than the denominator (or the numerator and denominator are the same number). In other words, if the numerator and denominator are not the same, an improper fraction is a number greater than 1. So, for example, $\displaystyle\frac{5}{4}$ can be changed to $\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$.
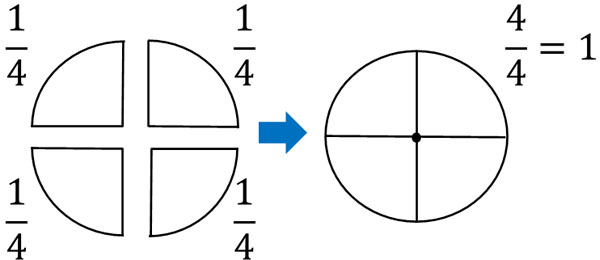
The fraction with the same numerator and denominator is 1. As shown below, four $\displaystyle\frac{1}{4}$ will result in $\displaystyle\frac{4}{4}$ and we know that $\displaystyle\frac{4}{4}=1$.
So, let’s separate an improper fraction into an integer and a proper fraction. For example, how do we turn $\displaystyle\frac{5}{4}$ into a mixed fraction? First, let’s split $\displaystyle\frac{5}{4}$ into an integer and a proper fraction. It will look like this.
- $\displaystyle\frac{5}{4}=\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$
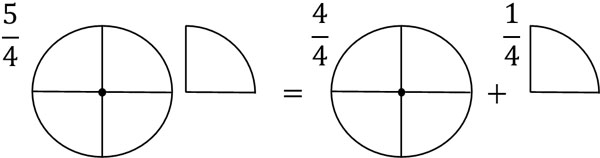
Also, $\displaystyle\frac{4}{4}=1$. Therefore, $\displaystyle\frac{5}{4}$ can be changed to a mixed fraction as follows.
- $\displaystyle\frac{5}{4}=\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}=1\displaystyle\frac{1}{4}$
In this way, we can take an integer from an improper fraction and turn it into a mixed fraction.
How to Convert a Mixed Fraction to an Improper Fraction
On the other hand, how can we convert a mixed fraction to an improper fraction? Earlier, we explained how to convert an improper fraction to an integer. To review, it looks like the following.
- $\displaystyle\frac{6}{2}=6÷2=3$
- $\displaystyle\frac{20}{5}=20÷5=4$
To change from integers to improper fractions, do the reverse of this calculation. Specifically, multiply the integer by the denominator and use the answer as the numerator. As a result, you can change an integer into a fraction.
For example, how can we change 3 into a fraction of the form $\displaystyle\frac{□}{4}$? In this case, multiply the integer 3 by the denominator 4, and put the resulting answer in the numerator.
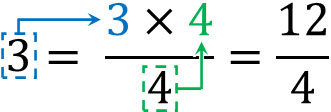
By using an integer and a denominator in this way, we can convert an integer to a fraction. Since $\displaystyle\frac{12}{4}=12÷4=3$, we know that the conversion to a fraction is correct.
Also, the mixed fraction has an integer part. For example, $2\displaystyle\frac{2}{5}$ means the same as $2+\displaystyle\frac{2}{5}$. So let’s change 2 to an improper fraction. To turn 2 into the form $\displaystyle\frac{□}{5}$, we multiply the integer by the denominator. This gives us the following.
- $2=\displaystyle\frac{2×5}{5}×\displaystyle\frac{10}{5}$
Therefore, we can change a mixed fraction to an improper fraction as follows.
- $2\displaystyle\frac{2}{5}=\displaystyle\frac{10}{5}+\displaystyle\frac{2}{5}=\displaystyle\frac{12}{5}$

If you are not familiar with it, you will not be able to convert between improper fractions and mixed fractions quickly. So, make sure that you can convert fractions by solving calculation problems over and over again.
Understanding the Concept of Fractions
When learning fractions for the first time, there are a number of concepts that you need to remember. Although it can be hard, fractions are used a lot in our daily lives. When counting numbers less than one, fractions make calculations easier.
So let’s try to understand the relationship between numerator and denominator. Fractions always have a numerator and a denominator.
Also, fractions have the same meaning as division. You should be able to convert a division into a fraction. It is also important to be able to convert a fraction into a division.
If you can do these, you will be able to convert improper fractions into integers and mixed fractions. You can also convert mixed fractions into improper fractions. Understand how to change the form of a fraction.