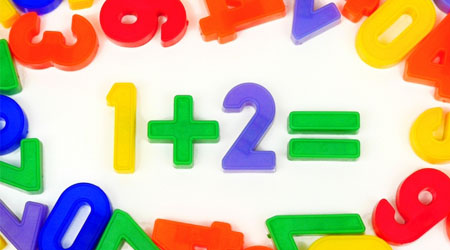After learning multiplication, we will study integer division in elementary school arithmetic. 1, 2, 3, etc., are integers, and we use these numbers to do calculations.
The meaning of division is the same as multiplication. In other words, if you can’t do multiplication, you can’t do division. Understand that division is an advanced problem of multiplication. It is also necessary to learn about the remainder in the division.
In this section, we will explain how to calculate division in elementary school math.
Table of Contents
Division with Integers: Solving Problems with Multiplication
When we do division, we use the symbol ÷. In integer division, the following calculation is used.
- $12÷3=□$
What does this mean? $12÷3$ means how many you get when you divide 12 by 3. For example, there are 12 cakes, and we divide them into three pieces. Then you can divide it into four parts.
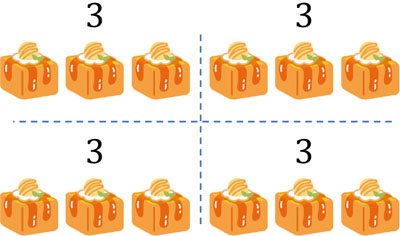
The division is used to split numbers.
So, how do we find the answer using division? Earlier, we explained that if you cannot do multiplication, you cannot do division. This is because multiplication must always be done when doing division.
For example, $12÷3$ can be interpreted as what you multiply 3 by to get 12. In other words, it is as follows.
- $3×□=12$
Thinking about what number goes into $□$ is division. Doing division also means doing multiplication. For example, let’s solve the following problem.
- $42÷6$
This question can be changed as follows.
- $6×□=42$
If we multiply 6 by 7, the answer is 42. Therefore, we know that the answer is 7. By using multiplication in this way, we can get the answer.
Remainders in Division
There are cases that we cannot divide by an integer when doing division. For example, the following equation is an example of this.
- $20÷3$
If we multiply 3 by 6, the answer is 18. On the other hand, if we multiply 3 by 7, the answer is 21. 20 is not divisible by 3. What should we do in such a case?
When doing division, if you can’t divide a number, you can use the remainder. The remainder is the number that remains after dividing. For example, in the case of $20÷3$, the answer is 6, and 2 is the remainder.
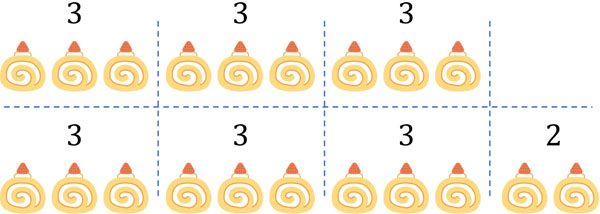
In this case, 2 is called the remainder. There are many cases that the number is not dividable, so the remainder is often used.
The remainder must always be smaller than the divisor. For example, let’s do the following calculation.
- $14÷4$
The answer is 3 R 2. Since $4×3=12$, 2 is the remainder.
It is important to note that the answer is not 2 R 6. In this answer, there is a remainder of 6 even though the divisor is 4. 6 (remainder) is a larger number than 4 (divisor), so the answer is wrong.

When dividing by 4, the remainder must always be a number less than 4. In other words, the remainder must be either 1, 2, or 3. For example, if the remainder is 6, you can subtract 4 once.
When you get the remainder, make sure that the remainder is smaller than the divisor. If the remainder is a number greater than the divisor, the answer is wrong.
How to Divide Using Long Division: Two-Digit and One-Digit Numbers
After learning how to do division, you should be able to do long division. As with multiplication, long division can be calculated by writing it down. For example, let’s do the following calculations.
- $76÷3$
In long multiplication, write the following.

Let’s solve this math problem. In division, let’s first focus on the largest digit. In 76, the largest digit is the tens place. How do we divide 7 by 3?
When we do $7÷3$, since $3×2=6$, we can multiply 3 by 2. So, let’s write 2 as follows.
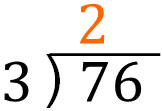
Then, the remainder is 1. The answer to $7÷3$ is 2 R 1.
In long division, we write the multiplication of divisor and answer below. When we do $7÷3$, we have to calculate $3×2=6$. So, in long division, we write 6 underneath. After that, we subtract as follows.
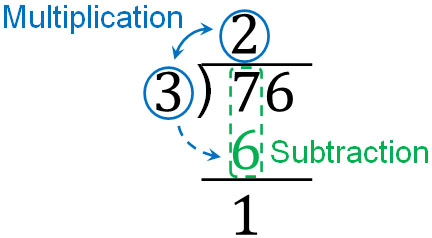
By subtracting, we can write down the remainder, which is 1.
The next thing we need to do is to calculate the remaining number: 6, which is the ones place out of 76. So, let’s write down 6 as follows.
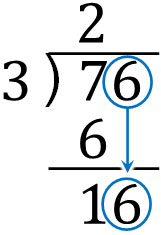
In this way, we get 16. In long division, divide 16 by 3. In other words, let’s calculate $16÷3$.
If we divide 16 by 3, what will be the answer? Since $3×5=15$, we know that 5 is the answer. So, write 5 as the answer. Also, as before, let’s write down 15, the answer to $3×5$, and subtract it. The result is as follows.
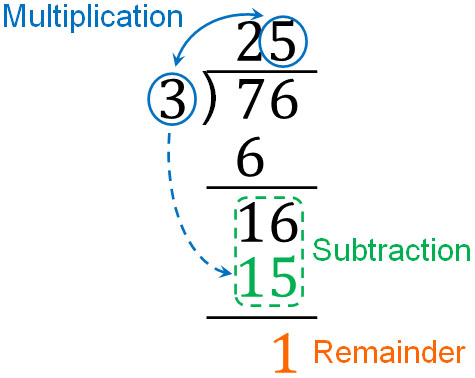
Thus, the answer is 25 R 1. In long division, the remainder appears at the bottom.
Make sure to align the upper and lower numbers when you do the math. When doing long division, you need to do multiplication and subtraction. In addition, we also put numbers down. If the upper and lower numbers are not aligned, calculation errors will occur.
Division by Two Digits: Two Digits and Two Digits
How do we divide two digits by two digits? Let’s try to solve the following math problem.
- $50÷12$
When you do the division, do it in the same way as before. Write it as follows.
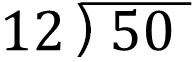
What should we multiply by for 12? Since $12×4=48$, we can multiply by 4. You need to predict what number you should multiply by. The result is as follows.
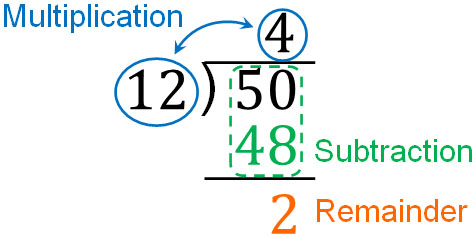
Thus, the answer is 4 R 2. Note that 2 (remainder) is less than 12 (divisor), so the answer satisfies the condition.
Three-Digit Division: Three Digits and Two Digits
If you can do a two-digit division, the next step is to do a three-digit division. How do you divide a 3-digit number by a 2-digit number? For example, let’s do the following calculation.
- $328÷21$
The way to do the calculation is the same. Let’s create the following equation.
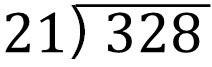
If we focus on the large digits in 328, we can divide 32 by 21. So, let’s do the math using long division. The result is as follows.
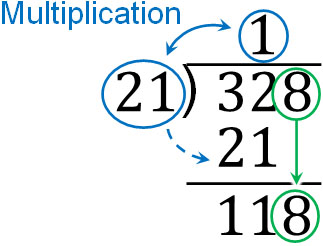
The next calculation is $118÷21$. What do we need to multiply 21 by to get the answer? This is a bit difficult to answer. So, let’s take a guess and come up with a random answer. If we multiply by 21, we get the following.
- $21×4=84$
- $21×5=105$
- $21×6=126$
The answer to $21×6$ is 126, which is greater than the number 118. So, we know that we should use $21×5=105$. Continuing with the long division, we have the following.
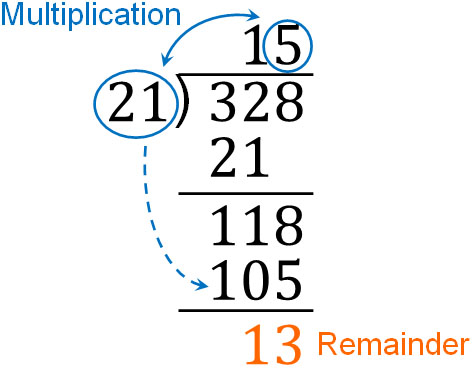
Thus, we found that the answer to $328÷21$ is 15 R 13. For numbers with large digits, the calculation of division is a little more complicated. So, let’s calculate them while predicting what numbers you should use.
Calculating the Division for Integers: Remainder and Long Division
In elementary school arithmetic, we learn division. Division means the same thing as doing multiplication. The division is also a multiplication problem. It is important to think about what numbers you need to multiply to get the answer.
However, unlike multiplication, the division can have a remainder. There are many calculation problems that you can’t divide, and in such cases, you need to find the remainder. The remainder must always be smaller than the divisor. It is important to understand this property.
In addition, when dividing a number by large digits, we need to use long division. There is a way to do this, so let’s learn how to do it.