One of the areas studied in mathematics is the inscribed angle. An angle using a circle is an inscribed angle, and by using the properties of the inscribed angle, we can calculate the angle.
There are properties of inscribed angles, which is called the inscribed angle theorem. If you do not understand the theorem, you will not be able to calculate the angle. Also, since there are advanced problems that use the theorem, you need to learn how to calculate angles in a circle, including special cases.
So, how can we use the inscribed angle theorem to solve calculation problems? Also, what is an inscribed angle?
In this article, we will explain the details of the inscribed angle theorem that we learn in mathematics.
Table of Contents
What Is an Inscribed Angle? Meaning of Arc and Central Angle
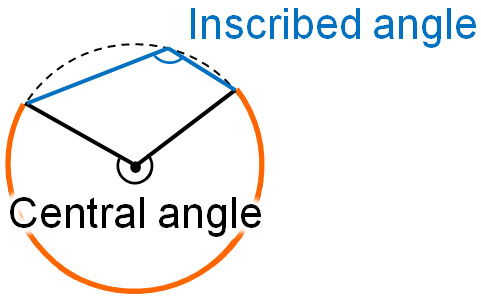
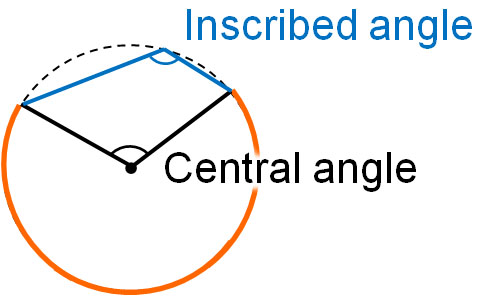
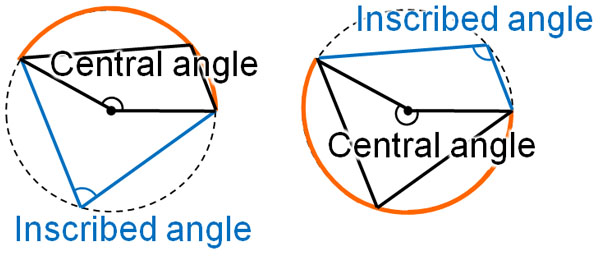
First of all, what is an inscribed angle? Before we understand the inscribed angle, we need to learn about the arc and the central angle. For a circle, the following parts are the arc and central angle.

When using the inscribed angle theorem, we will frequently use arcs and central angles. Therefore, it is important to understand which parts are arcs and central angles.
On the other hand, the inscribed angle refers to the following parts.

The arc AB is represented in mathematics as $\stackrel{\huge\frown}{AB}$. ∠APB corresponding to $\stackrel{\huge\frown}{AB}$ is called the inscribed angle. An inscribed angle always has an arc. Also, if there is an inscribed angle, there is always a central angle.
There Are Two Theorems for Inscribed Angles
What are the theorems of inscribed angles? Inscribed angles have two properties. They are as follows.
- Half of the central angle is always an inscribed angle.
- If the arc lengths are the same, the inscribed angles are always equal.
Let’s check the details of the inscribed angle theorem.
Half of the Central Angle Is Always an Inscribed Angle
The central angle is frequently used in the inscribed angle theorem. The reason for this is that there is a relationship between the inscribed angle and the central angle as follows.
- Inscribed angle × 2 = Central angle
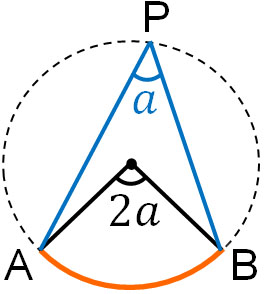
For example, if the inscribed angle is 30°, the central angle will always be 60°; multiply the inscribed angle by two to get the central angle. On the other hand, if the central angle is 80°, the inscribed angle is always 40°. Half of the central angle is the inscribed angle.
If the Arc Lengths Are the Same, the Inscribed Angles Are Equal
There is another theorem about the inscribed angle. For the same circle, if the arc lengths are the same, then the inscribed angles are equal. For example, the following inscribed angles are all the same.
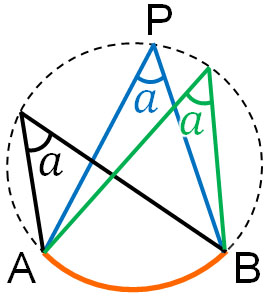
By using the same arc, we can find other angles. For example, for the following figure, what is the angle of $a$?
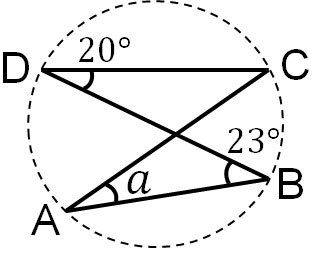
Focusing on $\stackrel{\huge\frown}{BC}$, we see that ∠BDC is 20°. Therefore, we know that the angle of $a$ is 20°.
If the Arc Is a Semicircle, the Inscribed Angle Is 90°
So far, we have discussed the most basic aspects of the inscribed angle theorem. However, there are more complicated calculation problems that use the inscribed angle theorem. Therefore, you need to be able to solve advanced problems. A typical example of this is the semicircle arc.
If the arc is a semicircle, we have the following.
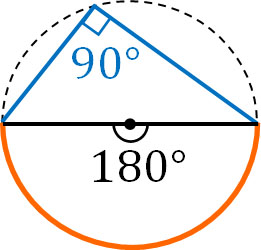
If the arc is a semicircle, the central angle is 180°. Therefore, the inscribed angle will always be 90°. Any inscribed angle is 90°, as shown below.
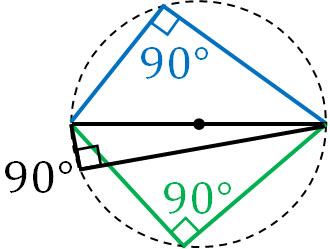
If the central angle has a special shape, it is difficult to find the inscribed angle. In any case, remember that if the arc is a semicircle, the inscribed angle will always be 90°.
How to Consider the Inscribed Angle, If the Arc Is Larger than a Semicircle?
On the other hand, how should we think about the inscribed angle when the arc is larger than a semicircle? In some cases, the arc length is small, while in other cases, the arc length is long, as shown below.
The idea is the same as what we have explained so far. If the arc is longer than a semicircle, the central angle will be greater than 180°. Therefore, the inscribed angle will always be greater than 90°.
The length of the arc is not necessarily shorter than the semicircle. There are cases where the arc length is longer than the semicircle, as in this case. Try to understand where the central angle is and where the inscribed angle is. For example, it is a mistake to think of the relationship between the central angle and the inscribed angle as follows.
In the figure above, the central angle is smaller than 180°. Nevertheless, the inscribed angle is larger than 90° in the figure. Therefore, the central angle and inscribed angle in this relationship are obviously wrong.
You need to find exactly where the central angle and inscribed angle are to be able to calculate the angle correctly. If the arc is longer than a semicircle, mistakes are more likely to occur. So when the central angle is greater than 180°, check to see if the inscribed angle is greater than 90°.
If You Add the Opposite Angles of a Quadrilateral Inscribed in a Circle, You Get 180°
By learning what we have discussed so far, you will be able to understand the properties of angles of quadrilaterals inscribed in a circle. For quadrilaterals inscribed in a circle, adding the opposite angles always results in 180°.

Why do the two angles add up to 180°? Let’s use the inscribed angle theorem we have learned so far to find out why.
For each angle, the relationship between arc, central angle, and inscribed angle is as follows.
The important thing to remember is that the two central angles add up to 360°. Also, the inscribed angle is half of the central angle. Therefore, two inscribed angles (opposite angles) add up to 180°.
Remembering the property that the opposite angles of a quadrilateral inscribed in a circle add up to 180° will help you when calculating angles. Although the quadrilateral must be inscribed in a circle, it is important to remember that the opposite angles always add up to 180°.
Arc Length and Inscribed Angle Are Proportional
For the same circle, the arc length and the inscribed angle are proportional. In other words, if the arc length is doubled, the inscribed angle will also be doubled.
It is easy to understand that the central angle is proportional to the arc length. As shown below, if the central angle increases from 30° to 60°, the arc length doubles.

The arc length can be calculated using the circumference and the central angle. For example, if the diameter of the circle is $b$ and the central angle is 30°, the arc length is as follows.
- $b×π×\displaystyle\frac{30°}{360°}$
On the other hand, if the central angle is 60°, the arc length is as follows.
- $b×π×\displaystyle\frac{60°}{360°}$
Thus, if the central angle is doubled, the arc length is doubled. In the same way, if the inscribed angle is doubled, the arc length is doubled. The central angle is proportional to the arc length. Also, the central angle and the inscribed angle are proportional. Therefore, the inscribed angle is proportional to the arc length.
Similarly, if the central angle or inscribed angle is tripled, the arc length will be tripled. If the arc length is quadrupled, the central angle and inscribed angle will be quadrupled. Understand that arc length and inscribed angle are proportional.
Exercise: Using the Inscribed Angle Theorem to Calculate an Angle
Q1: Find the following angles.
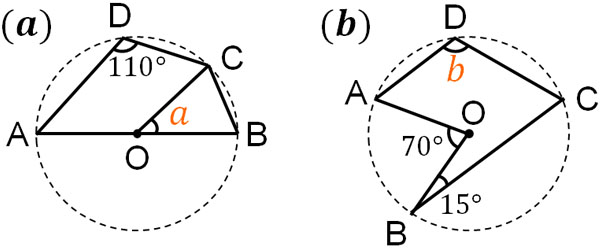
A1: Answers.
In the problem of finding an angle, randomly write down the angles you can find. This way, you will be able to get the angle at some point.
Also, there is more than one way to find the angle. It doesn’t matter which method you use, as long as you can find the answer.
(a)
The arc corresponding to ∠ADC is $\stackrel{\huge\frown}{ABC}$. The central angle is twice the inscribed angle, so the central angle is 220°.
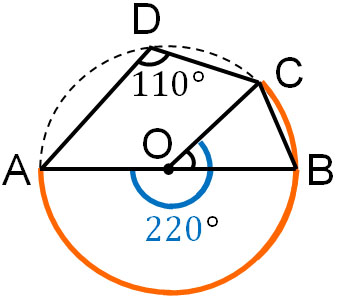
∠AOB is 180°. Therefore, $∠a$ is 40°.
- 220° – 180° = 40°
(b)
For complex problems, with the exception of a few geniuses, the answer cannot be given immediately. So, actively draw lines and write angles on the figure. In this way, you will eventually be able to get the answer.
If you draw a line from the center O, the length will always be the same. In other words, you can make an isosceles triangle. Since the base angles are the same in an isosceles triangle, we can find out the angles as follows.
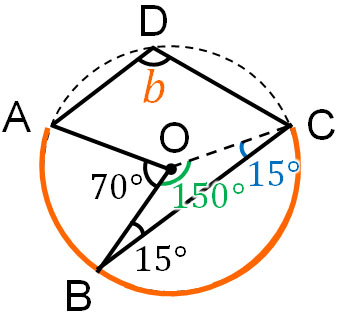
Since it is an isosceles triangle, ∠BCO is 15°. Therefore, we know that ∠BOC is 150°. On the other hand, the arc for $∠b$ is $\stackrel{\huge\frown}{ABC}$. The central angle corresponding to $∠b$ is as follows.
- 70° + 150° = 220°
Since the central angle is 220°, $∠b$ is 110°.
To get this answer, we need to randomly draw lines on the figure and find angles as mentioned above. From there, find the angle you need to get the answer and do the calculation.
Using the Property of Inscribed Angle to Calculate Unknown Angles
There are two theorems of inscribed angles to remember. The first is that half of the central angle is the inscribed angle. The other is that if the arc lengths are the same, the inscribed angles will always be the same.
However, although there are only two theorems for inscribed angles, there are several things you need to understand if you include advanced problems. It is important to understand beforehand what happens to the inscribed angle when the arc is a half-circle or longer than a semicircle.
Also, for a quadrilateral inscribed in a circle, the opposite angles always add up to 180°. Other than that, the arc length is proportional to the size of the inscribed angle.
Let’s use these facts to solve inscribed angle problems. Since inscribed angle problems can be complicated, it is best to find the answer by randomly writing down the angles you find.