An area that must be learned in mathematics is quadratic equations. Compared to linear equations, quadratic equations are more complicated to calculate.
In quadratic equations, there are multiple ways to get the answer. Square roots, factorization, and quadratic formulas are the most common ways to solve quadratic equations. When solving a quadratic equation, we must distinguish which method is the best way to solve it. This is why quadratic equations tend to be more difficult to solve than linear equations.
We can answer quadratic equations by using what we have learned so far, such as square roots and factoring. Also, since quadratic equation word problems are frequently given, we must be able to make equations.
We will explain how to solve quadratic equations, including not only how to answer the questions, but also how to solve word problems.
Table of Contents
An Equation Containing $x^2$ Is a Quadratic Equation
What is a quadratic equation? A mathematic equation is two expressions connected by an equal sign. If there is an $x^2$ in the equation, the equation is called a quadratic equation.
Therefore, the following are all quadratic equations.
- $x^2=9$
- $x^2+4x+3=0$
- $(x+5)^2=36$
Every expression has $x^2$. These equations are quadratic equations. There is a major difference between linear and quadratic equations; there are two answers in quadratic equations. For example, what is the answer to the following quadratic equation?
- $x^2=16$
The number that becomes 16 by squaring is 4. 42 is 16. Therefore, $x=4$ is the answer. However, squaring -4 also gives us 16. The answer to (-4)2 is 16. Therefore, $x=-4$ is also the answer.
It is important to understand that in quadratic equations, there can be two answers, not just one. Sometimes there is one answer, and sometimes there are two. This is the main difference between linear and quadratic equations.
Quadratic Equations Have Three Ways to Solve
In quadratic equations taught in mathematics, there are three ways to solve them. To be more specific, the following three methods are used.
- Using the square root.
- Using the factorization.
- Using the quadratic formula.
You can use any of these methods to get the answer. Each quadratic equation has a different way of answering, so be able to distinguish which method is best for you.
Solving Quadratic Equations Using Square Root
When answering quadratic equations, there is a way to solve them using square roots. There are only a few situations where you can use square roots. However, if you can use them, you can easily get the answer by using square roots.
To get answers by square root, the answer must be in the form of a quadratic equation as follows.
- $ax^2=b$
- $(x+a)^2=b$
If you can connect the squared equations with an equal sign, you can use square roots. The only way to get the answer is to add a root sign. You can get rid of the square numbers by adding a radical symbol, as shown below.

When solving quadratic equation problems, the easiest way to get the answer is to use square roots. Just add the root sign, and you will get the answer to the quadratic equation.
Factor the Left Side and Set the Right Side to 0
When answering a quadratic equation, a frequently used method is factorization. The use of factoring formulas is the way to get an answer.
There are four factoring formulas.
- $(x+a)(x+b)=x^2+(a+b)x+ab$
- $(x+a)^2=x^2+2ax+a^2$
- $(x-a)^2=x^2-2ax+a^2$
- $(x+a)(x-a)=x^2-a^2$
If you do not remember this formula, you will not be able to factorize it. In other words, you will not be able to solve quadratic equation problems. Remembering factoring formulas is essential for solving math problems.
So how do we factorize it? When factoring a quadratic equation, be sure to create the form $A=0$. The right side must be zero. For example, what is the answer to the following quadratic equation?
- $x^2+6x+5=0$
First, let’s factor this equation. Using the factoring formula, we can factor it into the following equation.
- $(x+1)(x+5)=0$
We need to answer the number of $x$ that satisfies this quadratic equation. What number can we substitute into $x$ that will result in zero?
In mathematics, any number has the property that if we multiply it by zero, the answer will be zero. So, if $(x+1)$ or $(x+5)$ is zero, the answer will be zero and match the right side.
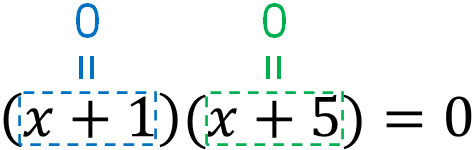
As for $x$ that makes $(x+1)$ or $(x+5)$ zero, they are -1 and -5. In other words, $x=-1,x=-5$ is the correct answer. Thus, after setting the right side to 0, we factorize the left side. Then we can get the answer to the quadratic equation.
Get a Complicated Answer by the Quadratic Formula
However, in some cases, the answer can be complicated.
If we use square roots, we must make a squared expression. If we use factoring, we have to factor the left side. So how do we find the answer to a quadratic equation if neither square root nor factorization can be used?
In this case, we use the quadratic formula. There is a formula for solving a quadratic equation. If $ax^2+bx+c= 0$, the formula that gives the answer to $x$ is the quadratic formula. The quadratic formula is as follows.
$$x={-b\pm\sqrt{b^2-4ac}\over2a}$$
It is a quite complicated formula, and this is the quadratic formula. You can substitute the numbers into the quadratic formula to get the answer.
For example, we have the following quadratic equation
- $2x^2+3x-4=0$
If you want to get the answer to this quadratic equation, substitute the numbers into the quadratic formula as follows.
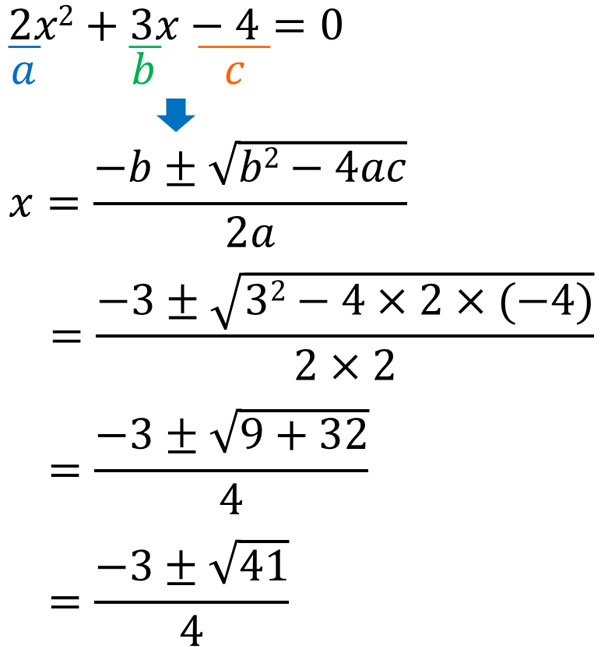
Even if we can’t use square roots or factorization, we can still get the answer by using the quadratic formula. Although the quadratic formula must be memorized, the answer can be obtained by substituting numbers.
It is possible to explain why the quadratic formula holds, using our previous knowledge of mathematics.
However, the formula to prove it is complicated. Also, no one proves the formula every time they use the quadratic formula to come up with an answer. Therefore, we will skip explaining why the quadratic formula is valid. The quadratic formula should be memorized.
Use a Simplified Quadratic Formula If $b$ Is Even
Note that when using quadratic formulas to solve problems, it is common to use a simplified quadratic formula if $b$ is even.
For even numbers, we can always divide by 2. So, set $b’$ after dividing $b$ by 2. In other words, $b’=\displaystyle\frac{b}{2}$. In that case, the following quadratic formula holds.
$$x={-b’\pm\sqrt{b’^2-ac}\over a}$$
The meaning of the quadratic formula is exactly the same, so we don’t always have to remember this formula. However, it is recommended to keep this simplified formula in mind when solving problems in mathematics. This formula will help you calculate faster and prevent miscalculations.
For example, try to solve the following quadratic equation using the quadratic formula.
- $2x^2+4x-1=0$
The following is a comparison of the different ways of solving the equation.
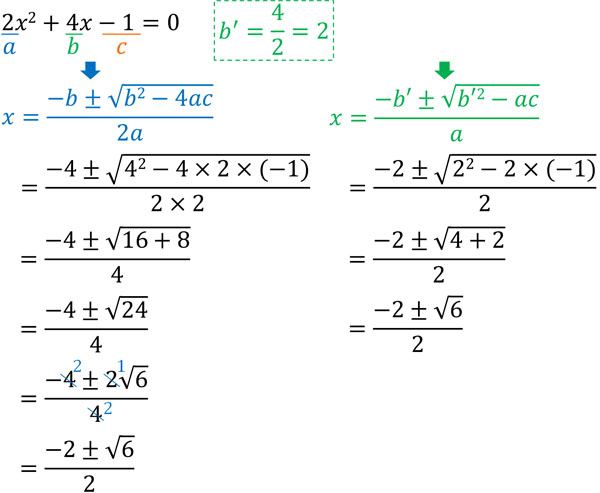
Both answers are the same. However, if we do not use the simplified quadratic formula, the calculation becomes more complicated. By doing prime factorization, we have to reduce the number in the root symbol. We also need to reduce the numbers in the fraction by dividing it.
In mathematics, the larger the number and the more steps there are, the easier it is to make miscalculations. To avoid miscalculations, most people use simplified quadratic formulas when answering quadratic equations.
How to Solve Quadratic Equation Word Problems
In this way, you will be able to determine which of the three methods is the best for you.
In addition, in mathematics, the most important thing is to use it in real life. Not only can we calculate it, but we should actually use it. For this reason, we need to be able to solve word problems. The way to solve a word problem is the same as for linear and simultaneous equations. The steps are as follows.
- Set the unknown number to $x$.
- Make quadratic equations from the problem statement.
- Solve quadratic equations.
If you have been solving word problems in mathematics so far, the way to solve quadratic equation word problems is the same.
Be Sure to Check If the Answer Is Optimal
However, in the case of quadratic equations, there is one thing you have to be careful about. That is, you must always check whether the answer is optimal or not.
As mentioned earlier, quadratic equations often give two answers. Then, one answer is frequently not optimal. Although the answer is given as a number, it is often not possible in the real world.
For example, let’s solve the following quadratic equation.
- The area of a rectangle with height $x$ cm and width $(x-2)$ cm is 24 cm2
The area of a rectangle can be found by the formula “vertical × horizontal.” Therefore, we can make the following quadratic equation.
- $x(x-2)=24$
Solving this quadratic equation gives us the following.
$x(x-2)=24$
$x^2-2x=24$
$x^2-2x-24=0$ (factorize)
$(x-6)(x+4)=0$
$x=-4,x=6$
As you can see, solving a quadratic equation yields two answers. However, $x=-4$ is not the answer. If $x=-4$, the equation $x(x-2)=24$ is satisfied. However, in the real world, the vertical length of a rectangle cannot be -4 cm. Therefore, the answer is only 6 cm.
If it is a temperature problem, the answer can be negative. In the real world, it is normal for the temperature to be negative. However, the vertical or horizontal length of the rectangle should not be negative.
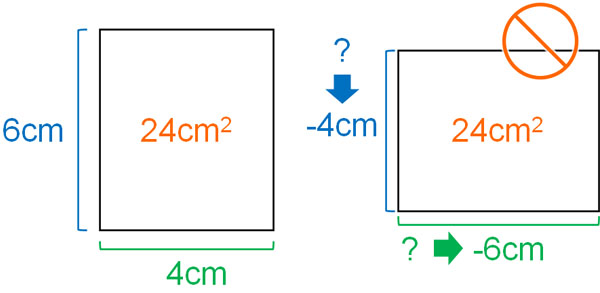
One thing to keep in mind with word problems in quadratic equations is that the answer we get is not always the correct answer. Even if we come up with an answer for $x$, be sure to check if the answer is suitable.
Exercises: Quadratic Equation Calculations and Word Problems
Q1: Solve the following quadratic equation.
- $2x^2-12=0$
- $(x+2)(x+4)=24$
- $x^2+5x+2=0$
A1: Answers.
There are three ways to solve quadratic equations. Find out which method is the best for you to solve the problem.
(a)
Solve using square roots.
$2x^2-12=0$
$2x^2=12$
$x^2=6$
$x=\sqrt{6},x=-\sqrt{6}$
(b)
Solve using factorization.
$(x+2)(x+4)=24$
$x^2+6x+8=24$
$x^2+6x-16=0$
$(x+8)(x-2)=0$
$x=2,x=-8$
(c)
Solve using the quadratic formula.
$x^2+5x+2=0$
$\displaystyle x={-5\pm\sqrt{5^2-4×1×2}\over 2×1}$
$\displaystyle x={-5\pm\sqrt{25-8}\over 2}$
$\displaystyle x={-5\pm\sqrt{17}\over 2}$
Q2: Solve the following word problem.
There is a rectangular land whose width is 4m longer than its vertical. On this land, make a path of 1 m wide and create four flowerbeds as follows.

If the area of all flowerbeds is 45 m2, how much is the vertical length of the land?
A2: Answer.
For example, if you work in architectural design, you have to do this kind of calculation. Mathematics is meant to be used in a practical way, and quadratic functions are used in many situations.
When solving this word problem, write the numbers in the figure. Otherwise, the problem will be difficult to solve. If the vertical length is $x$ m, we have the following.
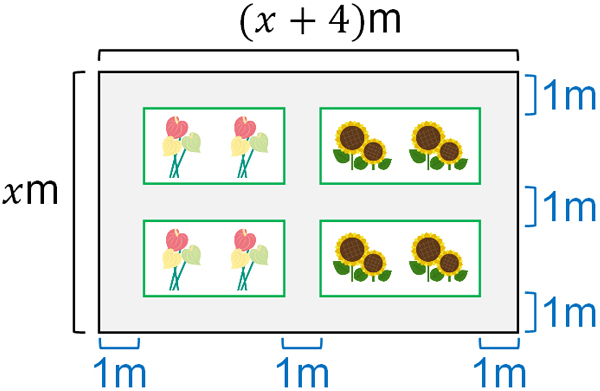
It is also difficult to understand if the four flowerbeds exist separately. So, let’s move all the flowerbeds to the top left, hypothetically.
The area of all flowerbeds will not change. In other words, moving the flowerbeds will not change the answer. When we actually build the flowerbed, we can return it to its original location. So let’s make a quadratic equation that takes into account the hypothetical situation of moving the flowerbeds. The result is as follows.

Since one path is 1 meter wide, the total width of the three paths is 3 meters. Therefore, the total vertical length of the flowerbed is $(x-3)$ m. And the total horizontal length of the flower bed is $(x+1)$ m.
Since the area of all flowerbeds is 45 m2, we can make the following quadratic equation.
- $(x-3)(x+1)=45$
Let’s solve this quadratic equation.
$(x-3)(x+1)=45$
$x^2-2x-3=45$
$x^2-2x-3-45=0$
$x^2-2x-48=0$
$(x-8)(x+6)=0$
$x=8,x=-6$
By solving the quadratic equation, we get the answer $x=8,x=-6$. However, the vertical length of the land cannot be -6 m. The number must be a positive number. Therefore, -6 m is unsuitable as an answer and must be excluded. So the correct answer is that the vertical length of the land is 8 meters.
In math problems, it is often very difficult to solve the problems by looking at the figures in the problem statement. However, by moving the figure, as in this exercise, the problem becomes easier and you can create a quadratic equation.
As long as the numbers are correct, you can transform the figure as you like. Try to think about how you can change the figure to make it easier to calculate.
Solving Quadratic Equations Calculating Problems
An expression with $x^2$ is a quadratic equation. When solving quadratic equation problems in mathematics, the difficulty level increases. This is because you have to use multiple knowledge that you have learned so far.
When solving quadratic equations, we must understand the following.
- Square roots
- Factorization
We also need to memorize the quadratic formula. There are three ways to solve a quadratic equation, and we have to distinguish which method is the best. In addition, there are two quadratic formulas, so we should be able to use both.
Furthermore, in quadratic equation word problems, one of the answers may be unsuitable. Compared to linear equations, quadratic equations require more precautions and are more complicated to solve. Understand how to solve quadratic equations.





