Fractions are frequently used in square root calculations. In the calculation of fractions, the denominator may contain the root symbol. In that case, if the root sign is still in the denominator, the answer is wrong.
When calculating the square root, if the denominator contains the radical symbol, it should be removed. This process is called rationalizing the denominator. In square root fractions, there is no problem if the numerator contains a square root, but it is not suitable if the denominator contains a radical sign.
So how do we rationalize the denominator? And why do we need to rationalize the denominator?
By learning these, we will be able to understand the procedure for correctly rationalizing the denominator in mathematics. We will explain how to rationalize the denominator.
Table of Contents
- 1 If There Are Radical Symbols in the Denominator, Make Rationalizing
- 2 Rationalizing of Addition and Subtraction with Two Terms in the Denominator
- 3 Why Do We Need to Rationalize the Denominator in Fractions?
- 4 Exercises: Calculation of Rationalizing the Denominator
- 5 In Square Root, Eliminate the Radical Sign in the Denominator
If There Are Radical Symbols in the Denominator, Make Rationalizing
In square root fractions, the denominator may contain a radical sign. For example, the following is the case.
- $\displaystyle\frac{1}{\sqrt{2}}$
In this fraction, the denominator contains $\sqrt{2}$. So let’s make it a fraction without a root sign in the denominator.

Square roots are irrational numbers. In mathematics, it is not good to have irrational numbers in the denominator. So, we change the number in the denominator to a rational number instead of an irrational number. Move the square root that exists in the denominator to the numerator. This is rationalizing the denominator.
In mathematics, if the root symbol remains in the denominator, the answer is incorrect. So be sure to rationalize the denominator.
Procedure for Converting the Square Root in a Denominator to an Integer
How do we rationalize the denominator? The way to do it is to multiply the denominator and the numerator by the same number. In fractions, it does not matter if we multiply or divide the denominator and the numerator by the same number. In fact, the following fractions are the same number.
- $\displaystyle\frac{1}{2}=\displaystyle\frac{2}{4}=\displaystyle\frac{3}{6}$
We can also consider $\displaystyle\frac{1}{2}=\displaystyle\frac{1×2}{2×2}$. Anyway, in fractions, the same number can be multiplied to the numerator and denominator.
Let’s take advantage of this property to rationalize the denominator. When squaring the square root, the root symbol is removed. So, we multiply the numerator and denominator by the same number as the square root in the denominator. The result is as follows.
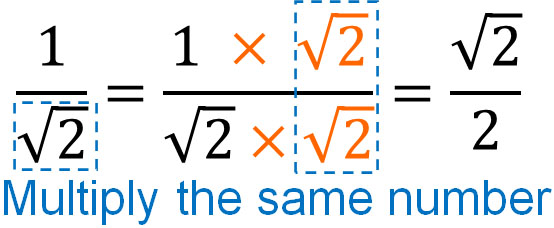
$(\sqrt{2})^2=2$. We can convert the number in the denominator to an integer by multiplying the same number. The way to rationalize the denominator is not difficult. All we have to do is multiply the square root in the denominator.
Smaller Numbers in the Radical Symbol Is Less Likely to Make Miscalculation
When rationalizing the denominator, the smaller the number in the root symbol, the fewer the miscalculations. We can reduce the number by doing prime factorization first.
For example, how can we rationalize the following fractions?
- $\displaystyle\frac{\sqrt{63}}{\sqrt{72}}$
When rationalizing the denominator, there are two ways to do it. One is to first reduce the number in the radical sign. The other way is to rationalize the denominator without first doing prime factorization. If we compare the two methods, we can see the following.
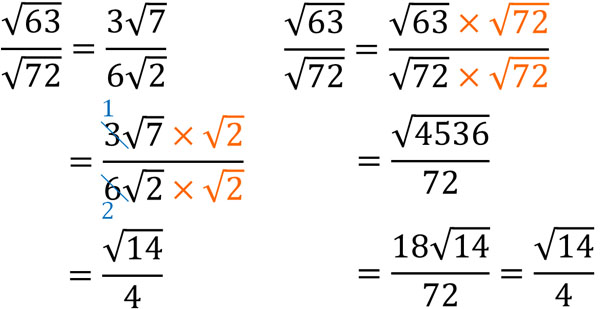
In this comparison, it is easier to calculate by first doing a prime factorization and then reducing the number in the root sign. In other words, there will be fewer calculation mistakes.
Any person can make mistakes in math calculations. So we have to choose ways to reduce the mistakes as much as possible. When we rationalize the denominator, if we first do prime factorization, we will make fewer calculation mistakes.
Rationalizing of Addition and Subtraction with Two Terms in the Denominator
An advanced problem when doing rationalizing the denominator is the case where there are two terms in the denominator. There is not only one radical sign, but it contains addition or subtraction.
For example, the following fraction has two terms in the denominator.
- $\displaystyle\frac{1}{3-\sqrt{2}}$
In this case, how should we calculate it? If there are two terms, use the factoring formula. To be more specific, use the following formula.
- $(x+a)(x-a)=x^2-a^2$
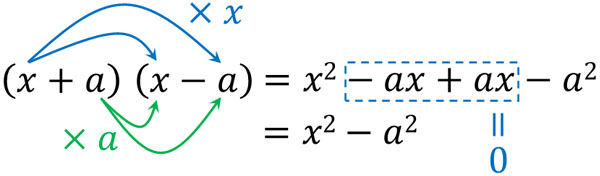
By using this formula, we can rationalize the denominator. For example, the previous equation can be calculated as follows.
$\displaystyle\frac{1}{3-\sqrt{2}}$
$=\displaystyle\frac{1\textcolor{red}{×(3+\sqrt{2})}}{(3-\sqrt{2})\textcolor{red}{×(3+\sqrt{2})}}$
$=\displaystyle\frac{3+\sqrt{2}}{3^2-(\sqrt{2})^2}$
$=\displaystyle\frac{3+\sqrt{2}}{9-2}$
$=\displaystyle\frac{3+\sqrt{2}}{7}$
Thus, we can rationalize the denominator by using the factoring formula. Even if there are two terms, we can rationalize the denominator in the following way.
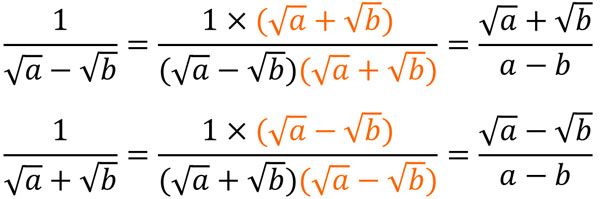
In some cases, the denominator contains square root addition or subtraction. In that case, use the factoring formula to rationalize the denominator.
Why Do We Need to Rationalize the Denominator in Fractions?
Why do we need to rationalize the denominator in square root fractions? What is the problem if the denominator has a radical symbol?
One reason why we need to rationalize the denominator is to make the numbers easier to understand. For example, it’s hard to understand what a number is in the following fraction.
- $\displaystyle\frac{1}{\sqrt{2}}$
Irrational numbers are numbers that go on forever. It is impossible to divide the numerator by such a number, and it is hard to imagine what kind of number it would be.
On the other hand, what if we do rationalizing the denominator and change the fraction to the following number.
- $\displaystyle\frac{\sqrt{2}}{2}$
Since it is an irrational number, the number in the numerator goes on forever. However, we can easily imagine what kind of number it would be. $\sqrt{2}≈1.41$. So we can see that $\displaystyle\frac{\sqrt{2}}{2}$ is about 0.7.
If there are irrational numbers in the denominator, it is difficult to imagine the numbers. On the other hand, even if there is a square root, it is easier to understand what kind of number it is if it is in the numerator.
When Making the Common Denominator, the Denominator needs to be Rationalized
Also, when making a common multiple of the denominators, it is preferable to rationalize the denominators. When adding and subtracting fractions, the denominators must be equal. If the denominators are the same, the properties of the fractions will also be the same.
However, when the denominator contains an irrational number, it is difficult to make the denominators match. For example, how can we do the following calculation?
- $\displaystyle\frac{1}{3}+\displaystyle\frac{1}{2+\sqrt{2}}$
In this situation, the calculation is difficult. The numbers cannot be matched because there is an irrational number in the denominator. So, let’s rationalize the denominator. Then we will be able to make the common denominator.
$\displaystyle\frac{1}{3}+\displaystyle\frac{1}{2+\sqrt{2}}$
$=\displaystyle\frac{1}{3}+\displaystyle\frac{1\textcolor{red}{×(2-\sqrt{2})}}{(2+\sqrt{2})\textcolor{red}{×(2-\sqrt{2})}}$
$=\displaystyle\frac{1}{3}+\displaystyle\frac{2-\sqrt{2}}{4-2}$
$=\displaystyle\frac{1}{3}+\displaystyle\frac{2-\sqrt{2}}{2}$
$=\displaystyle\frac{2}{6}+\displaystyle\frac{(2-\sqrt{2})×3}{6}$
$=\displaystyle\frac{2}{6}+\displaystyle\frac{6-3\sqrt{2}}{6}$
$=\displaystyle\frac{8-3\sqrt{2}}{6}$
If we make the denominator an integer, we can make common denominators for fractions. If an irrational number is in the denominator, we cannot make common denominators. Since we need to create common denominators to calculate fractions, we need to rationalize the denominators. If we don’t rationalize the denominator, we can’t calculate.
Exercises: Calculation of Rationalizing the Denominator
Q1: Rationalize the denominator.
- $\displaystyle\frac{4}{\sqrt{8}}$
- $\displaystyle\frac{\sqrt{3}}{\sqrt{24}}$
- $\displaystyle\frac{1}{\sqrt{6}+\sqrt{3}}$
A1: Answers,
If you understand what we have described so far, you can solve any problem easily.
(a)
$\displaystyle\frac{4}{\sqrt{8}}$
$=\displaystyle\frac{4}{2\sqrt{2}}$
$=\displaystyle\frac{2}{\sqrt{2}}$
$=\displaystyle\frac{2\textcolor{red}{×\sqrt{2}}}{\sqrt{2}\textcolor{red}{×\sqrt{2}}}$
$=\displaystyle\frac{2\sqrt{2}}{2}$
$=\sqrt{2}$
(b)
$\displaystyle\frac{\sqrt{3}}{\sqrt{24}}$
$=\displaystyle\frac{\sqrt{3}}{2\sqrt{6}}$
$=\displaystyle\frac{\sqrt{3}\textcolor{red}{×\sqrt{6}}}{2\sqrt{6}\textcolor{red}{×\sqrt{6}}}$
$=\displaystyle\frac{\sqrt{18}}{2×6}$
$=\displaystyle\frac{3\sqrt{2}}{12}$
$=\displaystyle\frac{\sqrt{2}}{4}$
(c)
$\displaystyle\frac{1}{\sqrt{6}+\sqrt{3}}$
$=\displaystyle\frac{1\textcolor{red}{×(\sqrt{6}-\sqrt{3})}}{(\sqrt{6}+\sqrt{3})\textcolor{red}{×(\sqrt{6}-\sqrt{3})}}$
$=\displaystyle\frac{\sqrt{6}-\sqrt{3}}{(\sqrt{6})^2-(\sqrt{3})^2}$
$=\displaystyle\frac{\sqrt{6}-\sqrt{3}}{3}$
In Square Root, Eliminate the Radical Sign in the Denominator
When dealing with square roots in mathematics, there are certain calculations that must be done. One of them is rationalizing the denominator. If the denominator contains a root symbol, it is wrong as it is. Be sure to rationalize the denominator.
Rationalizing the denominator makes it easier to figure out what kind of number it is. It also helps to create a common denominator for fractions, which allows us to add and subtract. It is important to understand why we need to rationalize the denominator.
The way to rationalize the denominator is simple. Multiply the numerator and denominator by the same number as the square root in the denominator. In this case, you can reduce the number in the root sign by prime factorization first to reduce miscalculations. Also, if the denominator has two terms, use the factoring formula.
There is a proper way to rationalize the denominator. Make sure you understand how to rationalize the denominator so that you can calculate the square root.





