In mathematics, we often think of figures in terms of three-dimensional objects instead of two-dimensional objects. In fact, everything around us is three-dimensional.
So, let’s make sure that we can calculate the size of three-dimensional objects. In elementary school geometry, we learn formulas to calculate the size of three-dimensional figures. Also, the size of a three-dimensional shape is called a volume. By using the formula, you will be able to calculate the volume.
So, let’s first calculate the volume of a cube and a cuboid. Then, we will be able to understand a capacity of a vessel. In this section, we will explain how to calculate the volume and capacity of cubes and cuboids.
Table of Contents
What Are Cubes and Cuboids?
First, let’s understand what a cube and a cuboid are. A cube is an object surrounded by six squares. Also, a cuboid is an object surrounded by six rectangles.
The following are a cube and a cuboid.

You should be able to calculate the size of such figures.
How to Calculate the Volume of a Cube and Cuboid
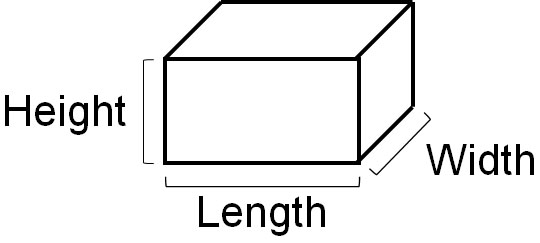
Understand that volume is the size of a 3D object. You will be calculating the size of an object that has height as well as length and width.
When calculating the volume of a cube or cuboid, use the following formula.
- The volume of a 3D object = length × width × height
For example, what is the volume of the following cube and cuboid?
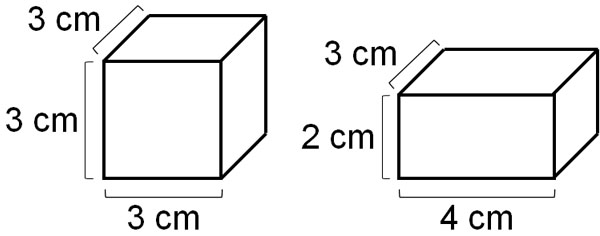
In the case of a cube, all the sides have the same length. So, let’s multiply the same number three times. Since the length of the side is 3 cm, the volume of the cube is as follows.
- $3×3×3=27$
Thus, the answer is 27 cm3. In an area, the length of a side is multiplied twice, so the unit is cm2. On the other hand, in calculating the volume, the length of the side is multiplied three times, so the unit is cm3.
Next, let’s calculate the volume of a cuboid, where the side lengths of the rectangle are different. So, let’s multiply the length, width, and height, respectively. The result is as follows.
- $4×3×2=24$
Thus, we see that the volume of the cuboid is 24 cm3.
Calculating the Capacity of a Vessel: The Volume of Water Filled in a 3D Object
After understanding volume, let’s learn about the capacity of a vessel. When a liquid (such as water) is poured into a vessel, the capacity indicates how much liquid can be poured into that vessel. The volume and capacity of a vessel are the same concepts, and the formula used is the same.
When calculating volume, we multiplied the length, width, and height respectively. When calculating the capacity of a vessel, multiply the length, width, and height of the vessel respectively as well.
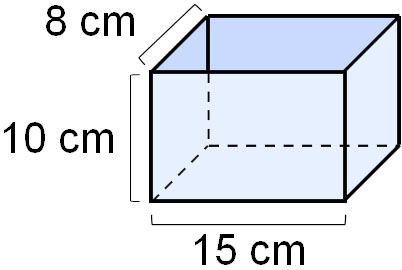
In this case, the capacity of a vessel is as follows.
- $15×8×10=1200$
Therefore, we can calculate that this vessel can be filled with up to 1200 cm3 of water. 1L is 1000 cm3, so we can also see that this vessel can hold 1.2L of water.
Cases Where Volume and Capacity Are Different
As mentioned earlier, the formula for calculating the volume and capacity of a vessel is the same. However, in reality, the volume and capacity may differ. This is due to the thickness of the container.
For example, what are the volume and capacity of the following container?
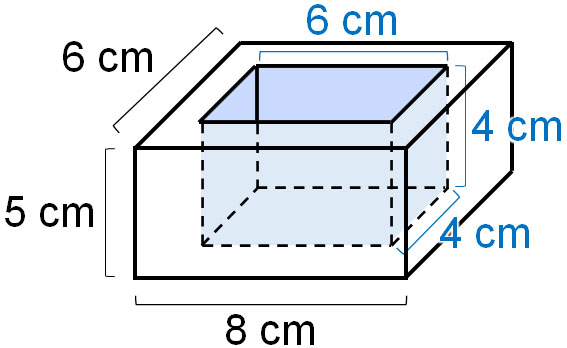
The volume is the size of the entire container. So, let’s multiply by the outside length of the container. Since it is 8 cm in length, 6 cm in width, and 5 cm in height, the volume is as follows.
- $8×6×5=240$
On the other hand, how can we calculate the capacity of a vessel? In capacity, it is important to know how much water can be filled. Only the inside of the container can hold water. So, let’s multiply the inside length of the container. Since it is 6 cm in length, 4 cm in width, and 4 cm in height, the volume is as follows.
- $6×4×4=96$
Thus, we can calculate the volume and capacity of a vessel. Understand that if the container has a thickness, the volume and capacity will be different.
Why Can We Calculate Volume and Capacity?
Why is it possible to calculate the volume and capacity of a vessel by multiplying the length, width, and height? Let’s find out why.
First of all, what is the volume of a cube with a side length of 1 cm?
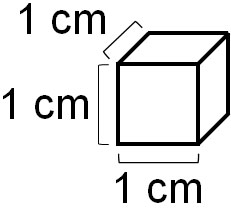
Since all the sides are 1 cm long, the volume of this cube is 1 cm3. Then, what is the volume of this cube if it is arranged as follows?
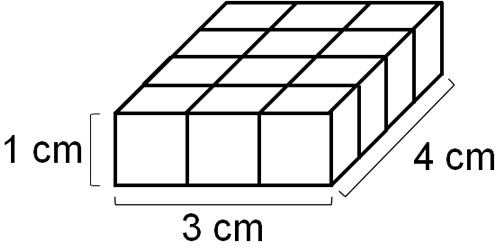
The total number of cubes is 12. Therefore, we know that it is 12 cm3. However, counting the number of cubes one by one is troublesome. So, let’s calculate the volume.
In contrast to the cube whose sides are all 1 cm long, the cuboid in the above figure has a height of 1 cm, but its vertical and horizontal lengths are different. So let’s multiply the length by the width in the same way as the area calculation.
- $3×4×1=12$
The height is 1 cm. However, multiplying by one does not change the answer. Therefore, in this cuboid, calculating the area is the same as calculating the volume.
Next, let’s consider a cuboid with a height of 3 cm instead of 1 cm. The result is as follows.

In this cuboid, there are three $3×4×1$ cuboids stacked on top of each other. Since the blocks are 3 cm high, we calculate the height in 3cm instead of 1cm as follows.
- $3×4×3=36$
When you think about it this way, you can understand why multiplying by the length, width, and height will allow you to calculate the volume.
Calculating the Side Lengths from the Volume
If the volume is known, there are cases where the side lengths can be calculated. For example, if the volume of the following cuboid is 16 cm3, what is the length of $a$?
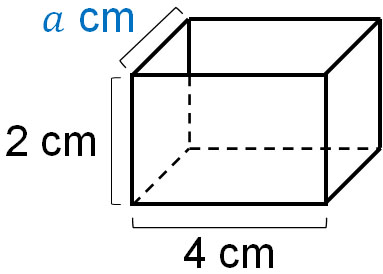
We already know the volume. Also, we know the length and height. So, if we set the width as $□$, we can make the following equation.
- $16=4×2×□$
Now, let’s calculate the value of $□$. Change it to the following equation.
- $□=16÷4÷2$
By calculating this expression, we can see that the width is 2 cm. In math, you can calculate the length of a side from its volume.
Learn How to Calculate Volume and Capacity
The objects around us are not flat but three-dimensional. Therefore, we should be able to calculate the size of three-dimensional figures. In particular, there are many cubic and cuboidal objects. If you look around your house, you will find that there are many cubic and cuboidal objects.
The size of a cube is the volume. When calculating volume, we can use the formula.
Another similar concept to volume is the capacity of a vessel. When a liquid is poured into a container, and the container is full, the capacity is how much liquid the container can hold. If you can calculate the volume, you can calculate the capacity of a vessel.
When you learn about cubes and cuboids, you should be able to calculate the volume. Also, understand why volume can be calculated by multiplying the length, width, and height. By learning these things, you will be able to calculate volume and capacity.