Sometimes we make a shape bigger or smaller. Although the shape is the same, the size of the figure and the length of the sides are different. There are two types of such figures: enlargement and reduction.
When you make a figure larger, it is an enlargement. On the other hand, when a figure is made smaller, it is a reduction. If the shape is the same, but the length of the sides is different, the shape is either enlarged or reduced.
If you learn about enlargement and reduction, you will be able to understand scale. Scale is what is used in maps. There are many times when you need to read a map. If you do not understand scale, you will not be able to read a map, and you will get lost.
So let’s learn the concepts of enlargement and reduction. This will help you to understand the size of shapes.
Table of Contents
Change in Side Lengths When Enlarging or Reducing
What is an enlargement? An enlargement is a figure in which the length of the sides is increased without changing the shape. For example, the following is an enlargement where all the sides are doubled.
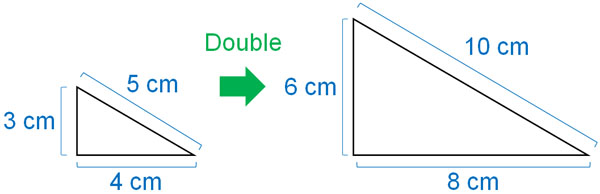
As you can see, the lengths of all the sides are doubled. Also, the shape of the figure is the same.
The size of the figure depends on how many times the length of the sides is increased. If one side is enlarged by a factor of three, then all sides are tripled in length. Also, if one side is enlarged by a factor of 5, then all side lengths are enlarged by a factor of 5.
On the other hand, reduction is the opposite of enlargement. In other words, the side lengths are not increased but decreased. The following is reduction.
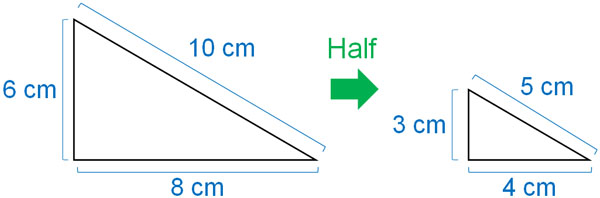
If one side is $\displaystyle\frac{1}{2}$ times in length, all sides will be $\displaystyle\frac{1}{2}$ times in length. Also, if one side is $\displaystyle\frac{1}{3}$ times in length, all sides will be $\displaystyle\frac{1}{3}$ times in length. This property is reduction.
The Length of the Corresponding Side Varies
The important thing to remember is that the length of the corresponding side varies. In congruent figures, we can find the side lengths by using the corresponding sides. Likewise, the corresponding sides are important for enlargement and reduction.
The shape of the figure is the same. Therefore, there are corresponding sides in enlargement and reduction. So, let’s understand that the length of the corresponding sides changes. For example, if the side length is doubled, the corresponding side is doubled.
The ratio of side lengths is the same in enlargement and reduction.
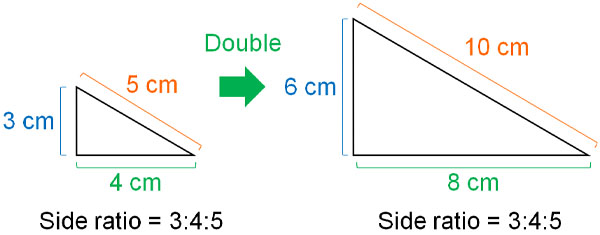
The shape of the figure is the same because the ratio of the side lengths does not change.
Angles Do Not Change in Enlargement and Reduction
As mentioned above, the shape of the figure is the same in enlargement and reduction. Therefore, while the length of the corresponding side increases or decreases, all the corresponding angles remain the same.
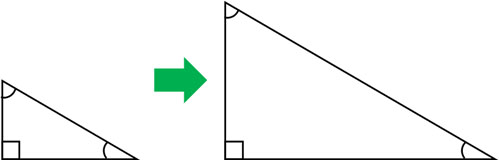
By the way, different angles will change the shape. Therefore, the following shapes are not the same in shape.
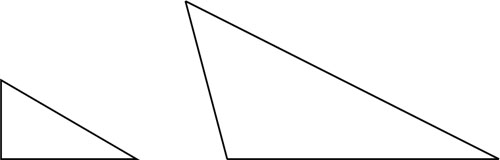
In enlargement and reduction, the shapes must be the same. Therefore, the angles must be the same. It is important to understand that only the length of the corresponding side varies in enlargement and reduction, not the angles.
Find the Corresponding Sides and Calculate the Lengths
In enlargement and reduction, find the corresponding sides. If you do, you can calculate the length. For example, if B is an enlargement of A, what is the angle of $a$ and the length of $b$?
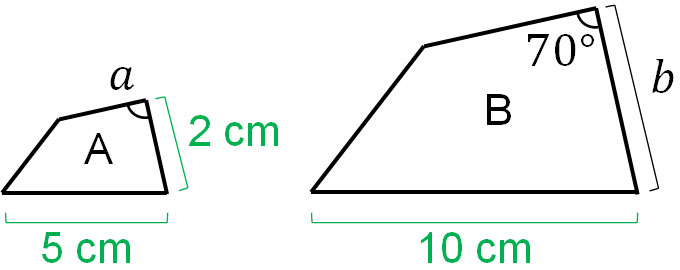
The magnitude of the corresponding angles are the same in enlargement and reduction. Therefore, $a$ is 70°. Also, the ratios of the corresponding sides are the same; if you look at A and B, you can see that doubling the side of A makes the side of B. Therefore, the length of $b$ is 4 cm.
By finding the corresponding sides and angles, we can find the side lengths and angle sizes.
On a Map, Scale Reduces Length Significantly
If you learn about enlargement and reduction, you will be able to understand scale. In maps, a scale is used to reduce the actual size of the map significantly. For example, the following is a map of New York City, USA.
If you check this map, you will see that the orange frame is marked as 1 km. In other words, the length of the orange frame on the map actually corresponds to 1 km. The map needs to show the actual world in a smaller size. That’s why we use a scale to show the world in a much smaller size.
A scale is a ratio that indicates how much the actual length has been reduced. For example, if the scale is “1:20000”, how many kilometers would 10 cm be on a map?
When we make a map, we set the length to $\displaystyle\frac{1}{20000}$ times. So to make it an actual length, we should multiply it by 20000. The result is as follows.
- 10 cm × 20000 = 200000 cm
Then, let’s change the unit from cm to km. 1 meter is 100 cm. Therefore, 200000 cm is 2000 m. Also, 1 km is 1000 m. Therefore, 2000 m is 2 km. Thus, we see that 2 km is the answer.
You can make a map by reducing the actual length of the land by the same percentage.
Learning the Concept of Enlargement and Reduction
In elementary school, students learn about enlargement and reduction. A figure with the same shape that is made bigger is enlargement. When a figure is made smaller, it is reduction.
The ratio of the lengths of the corresponding sides is the same in enlargement and reduction. Therefore, in enlargement and reduction, you can find the side lengths by comparing the figures. Also, the corresponding angles are the same. This is because if the angle changes, the shape changes. Therefore, if you know the corresponding angle, you can find the angle.
Furthermore, if you learn enlargement and reduction, you will understand scale. Scale is used in maps. In order to find out how long the distance shown on a map actually is, we need to learn about the concept of scale.
Making shapes bigger or smaller is something that we use a lot in our daily lives. One of the examples is maps. So let’s try to understand the relationship between enlargement and reduction and the concept of scale.