In calculating fractions, we often simplify fractions or find a common denominator. Even if you get an answer, it will not be correct if you do not simplify it. Also, you can’t add or subtract fractions without finding the common denominator.
When calculating fractions, you need to understand the concept of simplifying fractions and common denominators. So what is simplifying fractions? How do we find the common denominator?
In order to learn how to simplify fractions and find the common denominator, you must first learn about the properties of fractions. Then you will be able to simplify fractions and find the common denominator using your knowledge of common factors and common multiples.
There are two things you must use in fractions: simplifying fractions and common denominators. We will explain how to simplify fractions and find the common denominator.
Table of Contents
How to Simplify Fractions: The Answer Is the Same Even When Divided by the Same Number
First of all, what is simplifying fractions? Simplifying fraction is a process of reducing the number of fractions. For example, which is easier to understand, $\displaystyle\frac{2}{3}$ or $\displaystyle\frac{14}{21}$?
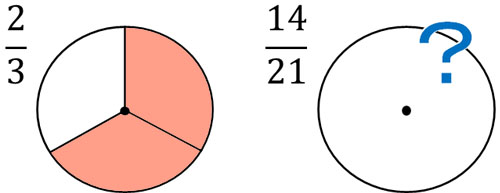
It is difficult to understand large numbers. This is the reason why we need to make numbers smaller in fractions.
So how can we reduce the number of fractions? To do this, divide the numerator and denominator by the same number. Fractions have the property that the number does not change even if the numerator and denominator are divided by the same number. For example, we have the following.
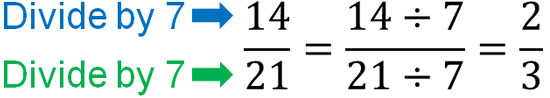
In this way, we can express $\displaystyle\frac{14}{21}=\displaystyle\frac{2}{3}$.
So why is the number the same even if the numerator and denominator are divided by the same number? A fraction is a number that indicates how many things are included after dividing.
For example, let’s compare $\displaystyle\frac{1}{3}$ and $\displaystyle\frac{2}{6}$. $\displaystyle\frac{2}{6}=\displaystyle\frac{2÷\textcolor{red}{2}}{6÷\textcolor{red}{2}}=\displaystyle\frac{1}{3}$, which means the two fractions are the same. Also, $\displaystyle\frac{1}{3}$ means to divide 1 into 3 equal parts. On the other hand, $\displaystyle\frac{2}{6}$ means to divide 1 into 6 equal parts and then add two $\displaystyle\frac{1}{6}$. Therefore, the figure is as follows.
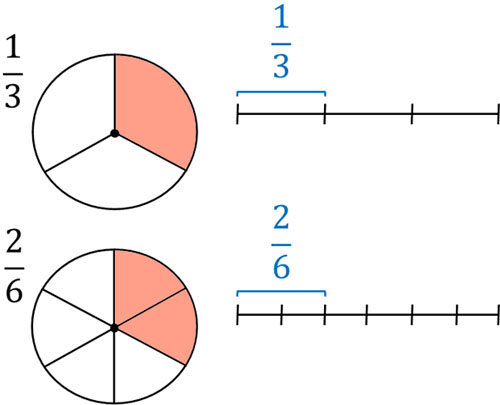
As you can see, the figure shows that $\displaystyle\frac{1}{3}$ and $\displaystyle\frac{2}{6}$ are the same number. This is the property of fractions, and dividing by the same number for the numerator and denominator does not change the answer.
Simplify Fractions by Finding a Common Factor and Then Dividing
How can we simplify fractions? The best way to simplify fractions is to find a common divisor. For example, how do we simplify the fraction $\displaystyle\frac{12}{18}$? Try to find a common divisor for the numerator and denominator.
Since 12 and 18 are even numbers, they can be divided by 2. Therefore, we can simplify the fractions as follows.
- $\displaystyle\frac{12}{18}=\displaystyle\frac{12÷2}{18÷2}=\displaystyle\frac{6}{9}$
However, we can further simplify this fraction by dividing the numerator and denominator by 3, since 6 and 9 have a common divisor of 3.
- $\displaystyle\frac{6}{9}=\displaystyle\frac{6÷3}{9÷3}=\displaystyle\frac{2}{3}$
Thus, we can simplify the fraction from $\displaystyle\frac{12}{18}$ to $\displaystyle\frac{2}{3}$.
When simplifying fractions, we can use the greatest common divisor to simplify fractions efficiently. In the case of $\displaystyle\frac{12}{18}$, the greatest common divisor of 12 and 18 is 6. Therefore, if we divide by 6, we can simplify the fraction with a single division.
However, if the numbers are large, it is difficult to find the greatest common divisor. Therefore, a common method is to use a small number such as 2 or 3 and see if it can be divided. In order to avoid miscalculations, it is an excellent way to simplify fractions by using smaller numbers instead of the greatest common divisor.
Multiplying the Numerator and Denominator by the Same Number Gives the Same Answer
So far, we have explained that dividing the numerator and denominator by the same number will give the same answer. This can also be said in reverse. In other words, if you multiply the numerator and denominator by the same number, the answer is the same. For example, the following are all the same numbers.

In fractions, if you divide the numerator and denominator by the same number, the result is the same. Similarly, if you multiply the numerator and denominator by the same number, the result is the same. Let’s understand this property.
Once you understand this property, you will be able to easily convert integers into fractions. For example, to convert 3 into a fraction of the form $\displaystyle\frac{□}{4}$, multiply the integer 3 by the denominator 4. You can turn an integer into a fraction by doing the following
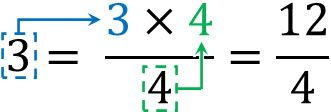
Why is it possible to do this? The reason for this is that if we multiply the numerator and denominator by the same number, we get the same number.
First, if we convert 3 to a fraction, we get $\displaystyle\frac{3}{1}$. If the denominator is 1, we usually omit the denominator. In any case, understand that you can convert an integer to a fraction in this way. Then, multiply the numerator and denominator by the same number. The result is as follows.
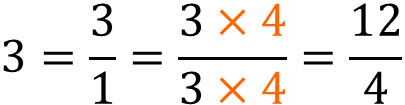
It is difficult to understand how to change an integer into a fraction if the explanation is “multiply the integer by the denominator.” On the other hand, if you learn about simplifying fractions and understand that multiplying the numerator and denominator by the same number will give the same answer, it will be easier to understand how to change an integer into a fraction.
Find the Common Denominator to Make the Denominator with the Same Number
Once you are able to simplify fractions, the next step is to find the common denominator. In simplifying fractions, we use common factors to make the numbers smaller. On the other hand, in finding the common denominator, we make the number larger by using common multiples.
As mentioned earlier, multiplying the numerator and denominator by the same number will result in the same number. We use this property in finding the common denominator.
Finding the common denominator means making the denominators the same. For example, how do we make the denominators the same for $\displaystyle\frac{1}{2}$ and $\displaystyle\frac{1}{3}$? Let’s change the fractions for $\displaystyle\frac{1}{2}$ and $\displaystyle\frac{1}{3}$ to the following, respectively.
- $\displaystyle\frac{1}{2}=\displaystyle\frac{1×3}{2×3}=\displaystyle\frac{3}{6}$
- $\displaystyle\frac{1}{3}=\displaystyle\frac{1×2}{3×2}=\displaystyle\frac{2}{6}$
Thus, by multiplying the numerator and denominator of $\displaystyle\frac{1}{2}$ by 3, we get $\displaystyle\frac{3}{6}$. Also, multiply the numerator and denominator of $\displaystyle\frac{1}{3}$ by 2, we get $\displaystyle\frac{2}{6}$.
In this way, we can make the denominator the same. This is the finding the common denominator.
Addition and Subtraction Can Be Done with the Same Denominator
Why do we need to make the denominators the same by finding the common denominator? It is because if the denominators are not the same, we cannot add or subtract fractions.
For example, $\displaystyle\frac{3}{4}$ is the sum of three $\displaystyle\frac{1}{4}$. Also, $\displaystyle\frac{2}{4}$ is the sum of two $\displaystyle\frac{1}{4}$. Therefore, $\displaystyle\frac{3}{4}+\displaystyle\frac{2}{4}=\displaystyle\frac{5}{4}$.
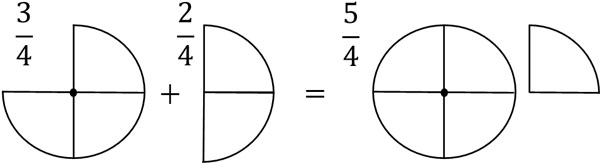
In the adding and subtracting fractions, the denominators must always be the same. If the denominators are different, as shown below, it is not possible to give a definite answer.
So, let’s find the common denominator to make the denominators the same. Once we find the common denominator, we can add or subtract since the denominators are the same.
For example, we cannot calculate $\displaystyle\frac{3}{4}+\displaystyle\frac{1}{2}$. On the other hand, if we consider $\displaystyle\frac{1}{2}=\displaystyle\frac{2}{4}$, and calculate it, we get the following equation.
- $\displaystyle\frac{3}{4}+\displaystyle\frac{1}{2}=\displaystyle\frac{3}{4}+\textcolor{red}{\displaystyle\frac{2}{4}}=\displaystyle\frac{5}{4}$
If the denominators are different, we have to find the common denominator in order to be able to add or subtract fractions.
Find the Least Common Multiple and Multiply the Numerator and Denominator
So how do we find the common denominator? In order to make a common denominator, we should use the least common multiple.
For example, how do we find the common denominator of $\displaystyle\frac{1}{4}$ and $\displaystyle\frac{1}{6}$? When finding the common denominator, let’s focus on the denominators; for the two fractions, the denominators are 4 and 6. So let’s try to find the least common multiple of 4 and 6. The multiples of each are as follows.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40…..
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42…..
Common multiples are 12, 24, and 36. Among these common multiples, we should use the least common multiple. 4 and 6 have a least common multiple of 12. So let’s change the fractions so that the denominator is 12. The result is as follows
- $\displaystyle\frac{1}{4}=\displaystyle\frac{3}{12}$
- $\displaystyle\frac{1}{6}=\displaystyle\frac{2}{12}$
Thus, change $\displaystyle\frac{1}{4}$ to $\displaystyle\frac{3}{12}$. Also, change $\displaystyle\frac{1}{6}$ to $\displaystyle\frac{2}{12}$. This allows us to add or subtract fractions since the denominators are the same.
When finding the common denominator, the denominator is generally set to the least common multiple. However, in some cases, you may not be able to find the least common multiple. In that case, you don’t necessarily need to make the denominator the least common denominator. Since you can add or subtract fractions as long as the denominators are the same, you can also use other common multiples to find the common denominator.
For example, to find the common denominator of $\displaystyle\frac{1}{4}$ and $\displaystyle\frac{1}{6}$, we can do the following.
- $\displaystyle\frac{1}{4}=\displaystyle\frac{6}{24}$
- $\displaystyle\frac{1}{6}=\displaystyle\frac{4}{24}$
Earlier, we set the denominator to 12, which is the least common denominator. This time, on the other hand, we set the denominator to 24, which is another common multiple. In this case, the denominators are the same, so we can add or subtract fractions.
One of the easiest ways to find the common multiple is to multiply the two denominators. For example, the denominators of $\displaystyle\frac{1}{4}$ and $\displaystyle\frac{1}{6}$ are 4 and 6. So if we do $4×6=24$, we can find 24 as the common multiple. This method is easier than finding 12, the least common multiple.
The key to finding the common denominator is to make the denominators the same. While using the least common denominator is the most common, you can use other common denominators.
Finding the Common Denominator to Determine the Size of Fractions
Once you can find the least common denominator, you will be able to distinguish the size of numbers when comparing fractions. For example, which of the following numbers is larger?
- $\displaystyle\frac{2}{5}$、$\displaystyle\frac{3}{8}$
If you have not learned how to find the least common denominator, you will not be able to solve this problem. On the other hand, if you understand how to find the least common denominator, you will be able to figure out which number is larger. To solve this problem, let’s find the common denominator. In other words, make the denominators the same. If the denominators are the same, you can determine the size of the fractions by comparing the numbers in the numerators.
The denominators are 5 and 8, and the least common multiple of 5 and 8 is 40. So let’s set the denominator to 40 for the two fractions. The result is as follows.
- $\displaystyle\frac{2}{5}=\displaystyle\frac{16}{40}$
- $\displaystyle\frac{3}{8}=\displaystyle\frac{15}{40}$
Thus, we see that $\displaystyle\frac{2}{5}=\displaystyle\frac{16}{40}$ and $\displaystyle\frac{3}{8}=\displaystyle\frac{15}{40}$. Also, since the denominators are the same, we can compare the numerators to find the size of the fractions.
Comparing $\displaystyle\frac{16}{40}$ and $\displaystyle\frac{15}{40}$, $\displaystyle\frac{16}{40}$ is the larger number. Also, $\displaystyle\frac{2}{5}=\displaystyle\frac{16}{40}$. Therefore, we know that $\displaystyle\frac{2}{5}$ is a larger number than $\displaystyle\frac{3}{8}$.
When comparing fractions, we can compare the size as long as the denominators are the same. We can also add and subtract them. This is why finding the least common denominator is so important when calculating fractions.
Using the Greatest Common Divisor and the Least Common Multiple to Simplify Fractions and Find the Common Denominator
Fractions are an important subject to learn in elementary school math. In fractions, there are many situations where we need to simplify fractions and find the least common denominator. So let’s understand how we can simplify fractions and find the common denominator.
An important part of simplifying fractions is the common divisor. For the numerator and denominator, dividing by the same number will result in the same fraction. So, let’s find the greatest common factor for both the numerator and denominator, and do the division. If it is difficult to find the greatest common divisor, you can use a smaller number such as 2 or 3 to do the division.
On the other hand, when adding or subtracting fractions, it is often necessary to make the denominators the same. In that case, find the least common denominator. If you multiply the numerator and denominator by the same number, you get the same result. Use this property to change the number of fractions. If you can’t find the least common denominator, you can also use other common denominators to make the denominator the same.
Simplifying fractions and finding the common denominator in fractions is essential knowledge. After learning the concept of fractions, make sure you understand how to simplify fractions and find the common denominator.