In elementary school math, students learn how to calculate decimals, including numbers smaller than one. We use decimals frequently in our daily lives.
First, let’s understand what decimals are. By learning how decimals work, we can understand when to use them.
Also, we need to be able to add and subtract decimals. Addition and subtraction require aligning digits, and we have to understand how to do it. So we will explain how to calculate decimals.
Table of Contents
What Are Decimals? Why Is It Necessary?
First of all, what is a decimal number? For example, the following numbers are decimals.
- 0.4
- 0.241
- 12.24
0.1 and 0.2 represent numbers less than 1. In other words, decimals are numbers that include less than 1. There are numbers between 0 and 1, and if we divide 1 into 10 equal parts, we get 0.1. Also, multiply 1 by $\displaystyle\frac{1}{10}$ to get 0.1.

If we divide 1 into 100 equal parts, we get 0.01; if we multiply 1 by $\displaystyle\frac{1}{100}$, we get 0.01. In short, there are numbers that are smaller than 0.1.
Also, if we divide 1 into 1000 equal parts, we get 0.001. Thus, by using decimals, we are able to express small numbers.
So, why do we need to learn decimals? It is because decimals are used a lot in our daily lives. For example, how many of the following cakes are there in total?

There are 3 and 0.2 cakes. Therefore, there are 3.2 cakes.
There are many situations that require the use of numbers smaller than 1. Decimals are important in math because they are often used.
The Position of Decimal Digits
Next, let’s learn how to read the digits in decimals. Each digit is called as follows.
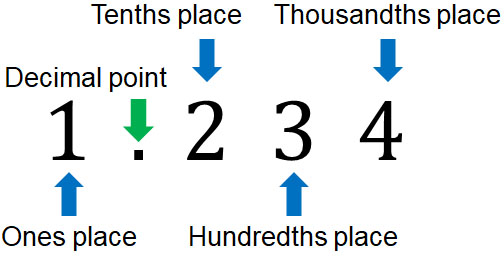
Decimals may also be expressed as $\displaystyle\frac{1}{10}$ths, $\displaystyle\frac{1}{100}$ths, etc., as follows.
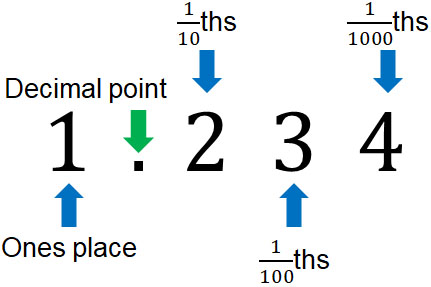
Whichever it is, make sure you understand the meaning.
How Decimals Work and Their Relationships
How do decimals work? And what is the relationship between the numbers?
As we have already discussed, multiplying 1 by $\displaystyle\frac{1}{10}$ gives us 0.1. Also, multiplying 1 by $\displaystyle\frac{1}{100}$ is 0.01. Furthermore, we can also consider 0.1 multiplied by $\displaystyle\frac{1}{10}$ to get 0.01. The relationship is as follows.
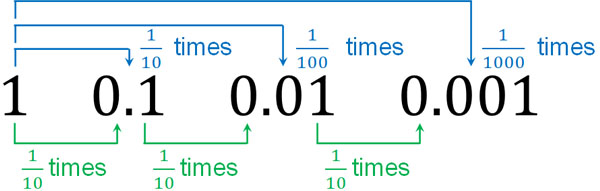
Also, if you multiply 0.1 by 10, you get 1. If you multiply 0.01 by 100, the answer is 1. Therefore, 0.01 multiplied by 10 gives us 0.1. The relationship is as follows.
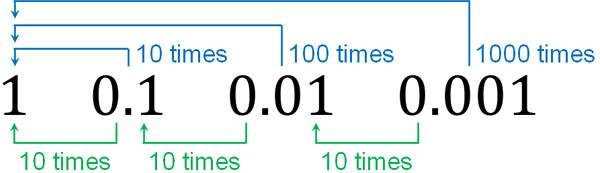
This is the relationship among them, and we must distinguish each digit.
For example, what does 1.3 look like? 1.3 is the sum of one 1 and three 0.1s. It is as follows.

We can also consider that 1.3 is the sum of thirteen 0.1s. As shown below, thirteen 0.1s add up to 1.3.

If we multiply 0.1 by 10, it becomes 1. So if there are thirteen 0.1s, the number becomes 1.3. Thus, it is important to recognize how decimals work.
How to Calculate Addition of Decimals
After understanding what we have learned so far, let’s try adding decimals. When we add decimals, we use the same addition method that we have learned so far. For example, we can do the following.
- $0.1+0.3=0.4$
- $0.2+0.5=0.7$
Although there is a decimal point, you can add decimals by adding numbers.
The important thing to remember is that you must align the digits. This is because if the digits are not aligned, the calculation cannot be done correctly. For example, when doing $21+243$, it would be a mistake to align the numbers to the left in long addition (or column addition).
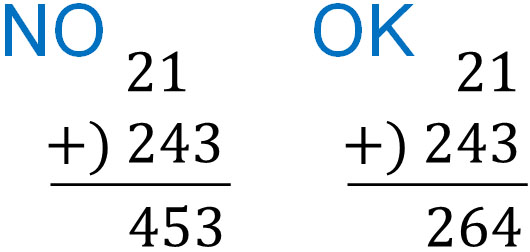
Therefore, let’s align the digits. In the case of the addition of decimals, we need to align the decimal point. For example, how would we calculate the following?
- $12.4+4.174$
When we do this calculation, we must align the digits. Create the following long addition.
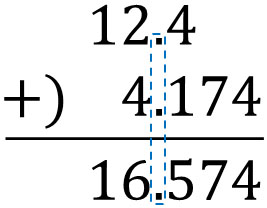
All you have to do is align the decimal point and then add the numbers. Let’s do the addition with the same digits.
It is important to note that when calculating decimals, you may have to delete zeros in some cases. If the rightmost number is zero, delete the zeros after adding. For example, we can calculate the following.
- $3.47+1.13=4.6$
- $12.75+2.25=15$
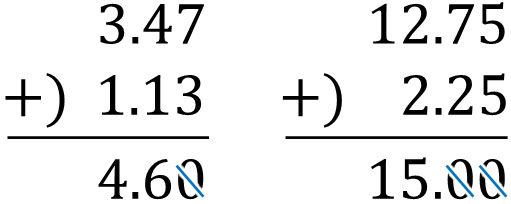
For your information, when the rightmost number is 0, you have to erase the 0; it’s the same in subtraction. In decimals, the zeros are hidden in the lower digits. When the number in the lower digits is zero, there is a rule to omit zero.
How to Calculate Subtraction of Decimals
On the other hand, how should we do subtraction? The method for subtracting decimals is the same as what we have learned so far. As with addition, you need to subtract by aligning the digits.
The important point is to align the decimal point. For example, let’s do the following calculation.
- $5.4-2.8$
If we make the long subtraction (or column subtraction), we get the following equation.
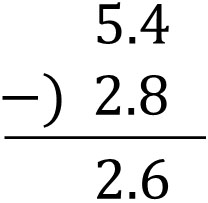
There is nothing particularly difficult about subtraction. Although there is a decimal point, the subtraction method is the same as the one we have learned before.
When the ones place becomes zero, be sure to write 0. The result is as follows.
- $1.5-0.9=0.6$
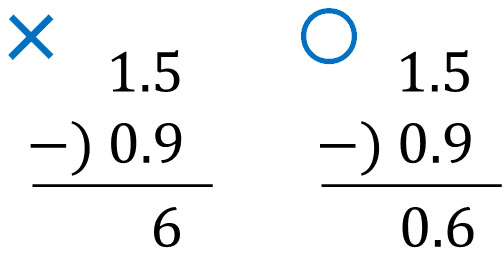
As explained before, you must always align the digits. Therefore, when calculating decimals, if the ones place is zero, be sure to write the decimal point and zero.
Subtracting Decimals with Multiple Digits
Let’s also learn how to subtract decimals with multiple digits. For example, how do we calculate the following?
- $19.3-2.147$
It is the same that we need to align the decimal point. In addition to that, let’s add zeros to make it 19.300 instead of 19.3. The result is as follows.
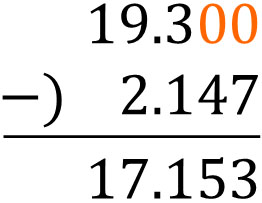
As explained earlier, there are zeros hidden to the right of the decimal point. Since the zeros goes on infinitely, we usually omit the zeros. However, if you subtract numbers with different digits, you can add 0 if necessary.
Learning the Concept of Decimals, Addition, and Subtraction
Learning the concept of decimals is important for us because we use them frequently in our daily lives, such as shopping. There are many situations where we need to use numbers smaller than one.
In this case, you need to be able to calculate decimals. By doing addition and subtraction, we can calculate the numbers we need. So be sure to align the decimal point and digits in your calculations. If you don’t, you will make a miscalculation.
There are many situations where decimals are used. Let’s understand the concept of decimals and be able to calculate them.