In math, we learn geometry. One of those areas is congruence. When there are two equal shapes, they are congruent shapes.
If we understand the concept of congruence, we can understand line and point symmetry. There are many shapes around us that have a line or point symmetry. So, try to understand what shapes are line symmetric and what shapes are point symmetric.
If you learn congruent figures, you will be able to understand the side lengths and the magnitudes of the angles. So, let’s discuss line and point symmetry.
Table of Contents
Shapes That Are Superimposed by Moving or Flipping Are Congruent
What is congruence? Congruence means that two figures are the same. For example, the following two figures are congruent.
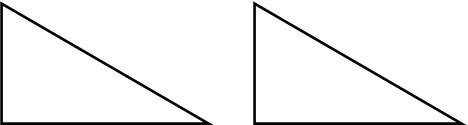
When two shapes can be completely superimposed on each other, they are congruent.
Also, when you move or flip a shape, the shapes that can be superimposed are congruent. For example, the following two figures are congruent.
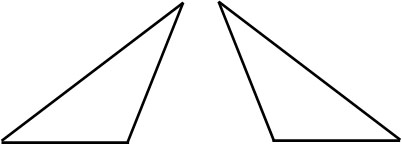
When finding congruent figures, understand that you can flip them over.
The Length of the Corresponding Sides and the Magnitude of the Angles Are the Same in Congruent Shapes
Why is it important to learn about congruent figures? The reason is that in congruent figures, the lengths of the corresponding sides and the sizes of the corresponding angles are the same. When two figures are congruent, the vertices that overlap are called corresponding points. The following are the corresponding points.
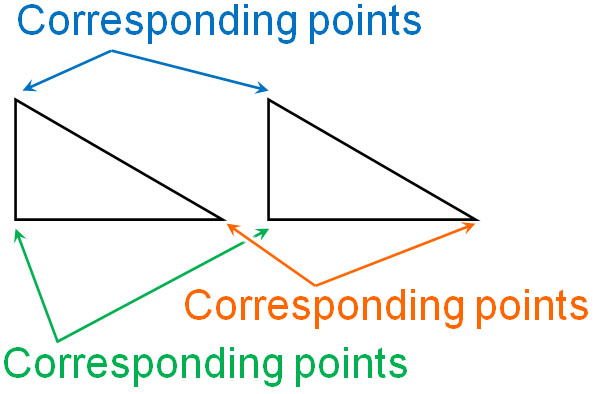
Also, when checking congruent figures, the same side is called the corresponding side. Corresponding sides have the same side length. Also, the same angle is called the corresponding angle. For corresponding angles, the size of the angle is the same.

Understand that in congruent figures, the length of the corresponding sides and the size of the corresponding angles are equal.
What Is Line of Symmetry and Point of Symmetry?
Once you understand congruence, you will be able to understand line and point symmetry. What are line symmetry and point symmetry? A simple explanation of each is as follows.
- Line of symmetry: When you fold a shape, the shapes are superimposed.
- Point of symmetry: When rotated 180°, the shapes are superimposed.
If the figures are superimposed, it means that they are congruent. Now, let’s take a look at line and point symmetry in detail.
If We Fold a Shape Using the Axis of Symmetry, the Superimposed Shape Is a Line Symmetric Shape
Line symmetry refers to shapes that superimpose when folded. For example, the following shapes are line symmetric shapes.

If you use the blue line to fold, both sides of the shape will overlap perfectly. In this case, the shape is line symmetry. The line used to fold a shape is called the axis of symmetry.
Some shapes may have more than one axis of symmetry. For example, a rectangle has two axes of symmetry, as shown below.
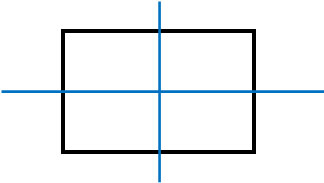
Understand that there may be more than one axis of symmetry.
Rotate 180° Using the Center of Symmetry, and the Overlapping Shape Is Point Symmetry
On the other hand, what is point symmetry? Point symmetry refers to a shape that perfectly overlaps when rotated 180° using the center of symmetry.
For example, the following figures are point symmetrical.

In a point symmetrical figure, there is a point that is the center. This point is called the center of symmetry.
So how do we know if a shape is point symmetric or not? To make it easier to understand, let’s turn the figure upside down. In this case, if we rotate the figure, we get the following.
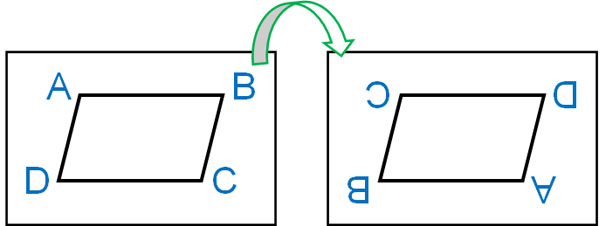
A figure that overlaps perfectly when turned upside down like this is a figure with point symmetry. Using the center of symmetry to rotate the figure by 180° is the same as turning the figure upside down.
In the case of point symmetry, the corresponding points, sides, and angles are as follows.

In a figure with point symmetry, the corresponding sides and angles are always on opposite sides.
In Line and Point Symmetry, the Corresponding Sides and Angles Are the Same
Why is it important to understand line and point symmetry? The reason for this is that line and point symmetry shapes have the following properties.
- Corresponding sides are equal in length.
- Corresponding angles are equal in size.
In line and point symmetry, the figures are congruent. In both line and point symmetry, the figures overlap perfectly. This means that the length of the sides and the size of the angles are the same. In other words, if you find congruent shapes, you can find the length of the sides.
For example, what are the values of $a$ and $b$ in the following figure?
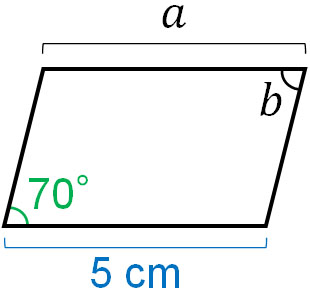
A parallelogram is a figure with point symmetry. The length of $a$ is 5 cm because the lengths of the corresponding sides are equal. Also, the corresponding angles are equal, so $b$ is 70°. Thus, we can find the side lengths and angles.
Find Congruent Shapes and Find Side Lengths and Angles
Shapes that are the same are congruent. If we find congruent shapes, we can find the side lengths and angles. This is because the lengths of the corresponding sides are equal, and the sizes of the corresponding angles are equal.
After understanding the concept of congruence, we will learn about line and point symmetry. When you fold a shape, if it perfectly overlaps, it is a figure with line symmetry. Also, if you use the center of symmetry to rotate the figure 180° and it perfectly overlaps, it is point symmetry.
These shapes have the property that the corresponding sides and corresponding angles are equal. Try to use this property to find the side lengths and angles.





