Fractions and decimals are two ways to express numbers less than one. Both are frequently used in math calculation problems.
The important thing to remember is that fractions can be converted to decimals. Decimals can also be converted to fractions. So, it is important to understand how to calculate them.
Also, in math, you should generally use fractions instead of decimals for calculations. In fact, in math problems where fractions and decimals are mixed, change all numbers to fractions. It is also common for students to use fractions to answer questions that contain only decimals.
Fractions can be used to represent any number. So, let’s understand the relationship between fractions and decimals.
Table of Contents
How to Convert Fractions to Decimals
First, let’s learn how to convert fractions to decimals. Fractions have the same meaning as division. Therefore, we can convert fractions into decimals by changing them into division expressions. For example, if we convert $\displaystyle\frac{1}{4}$ to a decimal, what value do we get?
So, let’s change the fraction to a division. The result is as follows.
- $\displaystyle\frac{1}{4}=1÷4=0.25$
As you can see, we can convert fractions to decimals by doing the division.
This calculation method is the same for mixed fractions, so let’s turn mixed fractions into an expression for division. In other words, change the mixed fractions to improper fractions and create an expression for division.
For example, how do we change $2\displaystyle\frac{1}{2}$ into an improper fraction? To change $2\displaystyle\frac{1}{2}$ to an improper fraction, we can do the following.
- $2\displaystyle\frac{1}{2}=\displaystyle\frac{4}{2}+\displaystyle\frac{1}{2}=\displaystyle\frac{5}{2}$
Next, let’s change $\displaystyle\frac{5}{2}$ to a decimal. The result is as follows.
- $\displaystyle\frac{5}{2}=5÷2=2.5$
There are other ways to calculate mixed fractions. However, since mixed fractions are not used in advanced mathematics such as middle school and high school mathematics, you should get used to calculating with improper fractions.
Fractions Cannot Be Converted to Decimals in Many Cases
There are many cases where it is not possible to convert a fraction to a decimal. For example, how do we convert $\displaystyle\frac{1}{3}$ to a decimal? It is not possible to convert $\displaystyle\frac{1}{3}$ to a decimal.
$\displaystyle\frac{1}{3}=1÷3$. So, doing this calculation, we get the following.
- $1÷3=0.3333333333…$
In this way, the numbers go on forever. When doing division, there are many cases where you cannot divide. In this case, you cannot change a fraction into a decimal.
What is important is the fact that even if the calculation is not divisible, you can still get the answer if it is a fraction. Even if you can’t find the answer with decimals, you can find the answer with fractions. For this reason, fractions are used more often than decimals in math.
How to Change a Decimal into a Fraction
Next, let’s understand how to change a decimal into a fraction. As mentioned earlier, when changing fractions to decimals, it is not always possible to convert them to decimals. On the other hand, conversion from decimals to fractions can always be done.
When converting decimals to fractions, remember the following relationships.
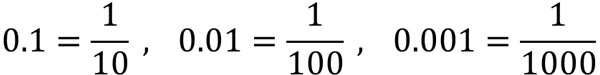
In fact, $\displaystyle\frac{1}{10}=1÷10=0.1$. Also, $\displaystyle\frac{1}{100}=1÷100=0.01$. So, for example, 0.2 is $\displaystyle\frac{2}{10}$.
You can create fractions by checking how many times you can move the decimal point to the right. For example, for 0.1, you can move the decimal point one place to the right. Also, for 0.01, you can move the decimal point two places to the right. For 0.001, you can move the decimal point three places to the right.
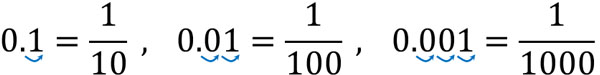
Then write zeros in the denominator equal to the number of times you moved the decimal point. In addition, put the number without the decimal point in the numerator.
For example, let’s change 0.152 to a fraction. If you check 0.152, you can move the decimal point three places to the right. Therefore, let’s write three zeros in the denominator. In other words, the denominator is 1000. You also write 152 in the numerator since you have to write the number without the decimal point.
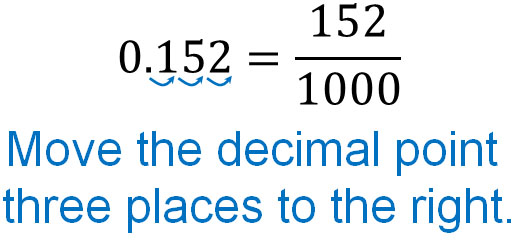
In addition, do not forget to simplify the fractions. It will look like this.
$\displaystyle\frac{152}{1000}$
$=\displaystyle\frac{152÷2}{1000÷2}$
$=\displaystyle\frac{76}{500}$
$=\displaystyle\frac{76÷2}{500÷2}$
$=\displaystyle\frac{38}{250}$
$=\displaystyle\frac{38÷2}{250÷2}$
$=\displaystyle\frac{19}{125}$
Thus, $\displaystyle\frac{19}{125}$ is the answer. When simplifying fractions with large numbers, it is difficult to find the greatest common divisor. Therefore, we can use smaller numbers such as 2 and 3 to simplify fractions until the numerator and denominator are not divided by the same number.
On the other hand, how can we change 1.25 into a fraction?
As before, let’s see how many times we can move the decimal point to the right. You will see that you can move the decimal point two places to the right. Also, let’s write a number in the numerator, omitting the decimal point. The result is as follows.
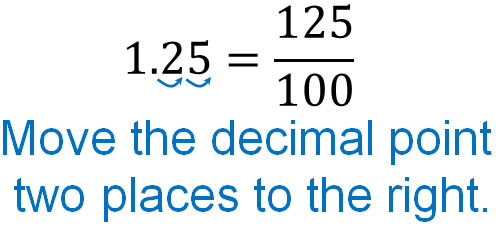
Thus, we get $1.25=\displaystyle\frac{125}{100}$. Also, if we simplify the fraction, we get the following.
$\displaystyle\frac{125}{100}$
$=\displaystyle\frac{125÷5}{100÷5}$
$=\displaystyle\frac{25}{20}$
$=\displaystyle\frac{25÷5}{20÷5}$
$=\displaystyle\frac{5}{4}$
In this way, if we simplify the fraction, we can get the answer.
Mixing Decimals and Fractions: Turning All Decimals into Fractions
After learning about decimals and fractions, you may have to solve a problem involving a mixture of decimals and fractions. How do you solve this problem?
When calculating numbers with different properties, it is easier to calculate them if you make their properties the same. So, change to decimals or fractions.
In general, in calculation problems where decimals and fractions are mixed, change all the numbers to fractions. As mentioned above, there are many cases where fractions cannot be changed to decimals. Decimals, on the other hand, can always be converted to fractions. This is why we change all decimals to fractions.
For example, how do we solve the following math problem where decimals and fractions are mixed together?
- $5.2÷\displaystyle\frac{3}{2}×\displaystyle\frac{5}{4}$
First, let’s turn the decimal into a fraction: $5.2=\displaystyle\frac{52}{10}$ if we turn 5.2 into a fraction. Therefore, the equation is as follows.
- $\displaystyle\frac{52}{10}÷\displaystyle\frac{3}{2}×\displaystyle\frac{5}{4}$
Also, dividing fractions must always be converted to multiplying fractions. So let’s use reciprocals and turn it into a multiplication expression as follows.
- $\displaystyle\frac{52}{10}\textcolor{red}{×\displaystyle\frac{2}{3}}×\displaystyle\frac{5}{4}$
Let’s calculate this. The result is as follows.

Thus, the answer is $\displaystyle\frac{13}{3}$. You can simplify the fractions in any order you want. In any case, if you can correctly change decimals to fractions, convert division to multiplication, and simplify fractions, you can get the answer.
Calculating Decimals and Giving the Answer in Fractions
As mentioned above, there are many cases where you cannot divide and cannot get the answer. In such cases, use fractions to get the answer.
For example, when dividing decimals by decimals, how do you give the answer? All calculations that cannot be divided should be answered with fractions. For example, let’s do the following calculation.
- $7.2÷1.4$
Even if you do this calculation, the answer will be 5.14285… and the numbers will go on forever. So, let’s make it a fraction as follows.
- $7.2÷1.4=\displaystyle\frac{7.2}{1.4}$
Then, make the denominator and numerator integers. If we multiply the numerator and denominator by the same number, the answer will be the same. So let’s multiply the numerator and denominator by 10.
- $\displaystyle\frac{7.2}{1.4}=\displaystyle\frac{7.2×10}{1.4×10}=\displaystyle\frac{72}{14}$
Next, let’s simplify the fractions.
- $\displaystyle\frac{72}{14}=\displaystyle\frac{72÷2}{14÷2}=\displaystyle\frac{36}{7}$
Thus, we get the answer. Fractions are often used in mathematical calculations because you can get the answer even if it is not divisible.
Understand the Relationship Between Fractions and Decimals and Perform Calculations
Fractions and decimals can be converted to each other. Fractions are also divisions, and by dividing, they can be converted to decimals. However, while all decimals can be converted to fractions, fractions often cannot be converted to decimals. This is because even if an expression cannot be divisible, it can be expressed as a fraction, and if it cannot be divisible, it cannot be expressed as a decimal.
So, let’s understand how to convert fractions to decimals. Also, when changing decimals to fractions, focus on the position of the decimal point.
In some cases, you may have to solve a calculation problem where fractions and decimals are mixed together. In this case, change the decimals to fractions. This is because, as mentioned above, all decimals can be converted to fractions.
Understand the relationship between fractions and decimals: Fractions and decimals are numbers that can represent numbers less than one. However, they have different properties, so let’s learn how to calculate them.