After learning addition, subtraction, multiplication, and division for positive and negative numbers, students need to be able to calculate expressions that mix each of them.
Addition, subtraction, multiplication, and division are collectively called the four rules of arithmetic.
In mathematics, we study the four rules of arithmetic (four arithmetic operations). After learning about positive and negative numbers, we have to understand the rules for calculating them in advance. In math calculations, there is some correct order of solving a problem that needs to be remembered.
So how should we calculate the four arithmetic operations of positive and negative numbers? We will explain this, including the rules of powers, priority, and parentheses.
Table of Contents
Learn the Important Rules in Four Arithmetic Operations
In order to do something, we need to learn the rules. For example, when you play football, you are not allowed to hold the ball in your hands. This is because such rules are set. If we follow the rules, fair play is possible.
Also, because people obey the law, the number of crimes can be reduced. If there are no laws (rules) where looting and robbery are punishable, many crimes will occur.
Similarly, there are rules in mathematics. By following the rules, we can calculate correctly. Some of the rules we need to recognize in the four rules of arithmetic are that we must calculate in the following order.
- Calculating powers.
- Calculate inside parentheses.
- Do multiplication and division.
- Do addition and subtraction.
If you don’t follow this order, you will not be able to get the correct answer in mathematics. For example, the following just changes the place of the parentheses, and the answer is different.
- $(2×3)+4=10$
- $2×(3+4)=14$
Changing the position or type of symbols can lead to different answers. Four rules of arithmetic are important in all sorts of situations, including high school and college math, bookkeeping, and programming. So let’s learn the math rules.
Reason for Calculating Powers First
The first thing to consider in the four rules of arithmetic is powers. If there are powers in the equation, they must be calculated first.

Why do we have to calculate the powers first? Because it is a single number. If power is in an equation, it is impossible to answer without calculating the power first.
In mathematics, you can not calculate unless you make the number clear. For example, we need to calculate the power first, as follows.
- $2×\textcolor{red}{4^2}=2×\textcolor{red}{(4×4)}=2×\textcolor{red}{16}=32$
The answer to 42 is 16. So, we must change 42 with 16 beforehand. Since $4^2=16$, this calculation must be done first.
On the other hand, if we ignore the power calculation and try to multiply the numbers, we will get the wrong answer. For example, the following calculation is wrong.
- $\textcolor{red}{2×4}^2=\textcolor{red}{8}^2=8×8=64$
Even though 42 is a single number, if you multiply or divide it by another number without calculating the powers, you will get the wrong answer. For this reason, if there are powers in the equation, we must calculate them first.
Calculating Inside Parentheses
There are many situations in mathematics where parentheses are used. The important thing is to give priority to the calculation inside the parentheses.
The expression inside the parentheses is considered as a single number. Although the expression is written inside the parentheses, it must be calculated first because the expression is considered as a single number.
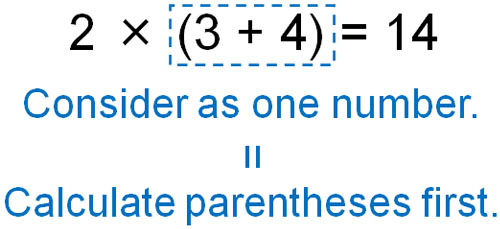
We explained about powers that they must be calculated first because they are considered a single number. The same is true for the calculation inside the parentheses. Since it is a single number, the number in parentheses must be calculated first to get the answer.
For example, let’s try to solve the following question.
- $2×\textcolor{red}{(7-3)}=2×\textcolor{red}{4}=8$
You can get the correct answer by calculating $(7-3)=4$ first. On the other hand, it is wrong to ignore the parentheses and calculate the multiplication first, as shown below.
- $\textcolor{red}{2×(7}-3)=14-3=11$
If there are parentheses, the calculation inside the parentheses must be done first.
In addition, sometimes parentheses can contain powers. In this case, we can calculate the power and then calculate the inside of the parentheses. For example, the following.
- $2×\textcolor{red}{(7-3^2)}=2×\textcolor{red}{(7-9)}=2×\textcolor{red}{-2}=-4$
Since powers are a single number, it is impossible to calculate in parentheses without calculating powers. Therefore, understand that the calculation of powers must be done first.
Multiplication and Division Are Calculated Before Addition and Subtraction
The next calculation to be done is multiplication and division. Multiplication and division must be done first, and addition and subtraction later. Why does multiplication (or division) take precedence? It is because we have to take units into account.
When calculating in mathematics, many problems do not have units. However, in real life, there are units. Because mathematics is used in everyday life, we have to be aware of units. The equations just omit the units, and the units are hidden.
There are only a few situations in our daily lives where we have to add or subtract. This is because, in order to add or subtract, the units must be the same. For example, if you add 3 kg and 5 kg, you get 8 kg. But you can’t add 3 kg and \$2. This is because the units are different.

What is important is the fact that we are not allowed to add or subtract freely.
On the other hand, multiplication (or division) can be calculated, even if the units are different. For example, if you buy 3kg of bananas that cost \$2.00 per kilogram, you can calculate as follows.
- $\$2 × 3kg = \$6$
Although we use kg in the expression for multiplication, the unit of the answer is dollars. In multiplication (or division), we can change the units.
As mentioned earlier, addition and subtraction can be done in the same units. The reason why multiplication and division must be done before addition and subtraction are because the units must be the same.
-Do Addition and Subtraction Last
Make sure to understand these rules and calculate them. After calculating powers, parentheses, multiplication, and division, the last step is addition and subtraction.
Addition and subtraction are done after all the numbers have been calculated and the units become the same. Understand that there are these rules in mathematics.
Calculating from Left to Right? Convert Division into Multiplying Fractions
So far, we have explained the order of precedence and the reasons for calculating positive and negative numbers (four arithmetic operations). However, some people may be taught the rule of calculating from left to right in addition to the previous explanation. However, it’s okay to forget this rule.
For addition and multiplication, the answer is the same, no matter how you calculate it. As mentioned above, you must follow the rules about multiplication that must take precedence over addition and subtraction. However, whether you calculate from the left or the right, the answer is the same.
Nevertheless, why do we have to calculate positive and negative numbers in four arithmetic operations, starting from the left? That’s because it includes division. When division is included in the equation, we cannot get the correct answer unless we calculate it from the left.
For example, let’s do the following calculation.
- $\textcolor{red}{6÷2}×3=\textcolor{red}{3}×3=9$
Calculating from left to right, the answer is 9. On the other hand, if we calculate from right to left, what happens? The result is as follows.
- $6÷\textcolor{red}{2×3}=6÷\textcolor{red}{6}=1$
As you can see, the answer depends on whether you are calculating from the left or the right. If you check the equation, you will see that even though it must be divided by 2, the wrong calculation shows that it is divided by 6. Because of this calculation error, we are generally told to calculate from left to right.
Don’t Use Division, Convert It All to Multiplying Fractions
But in fact, a division is inconvenient in mathematics. There are so many cases where it cannot be divided, and it is not useful. Therefore, in reality, a division is rarely used in mathematics, including in junior high school, high school, and college.
As an alternative to division, fractions are used. Division can be converted into multiplying fractions, as shown below.
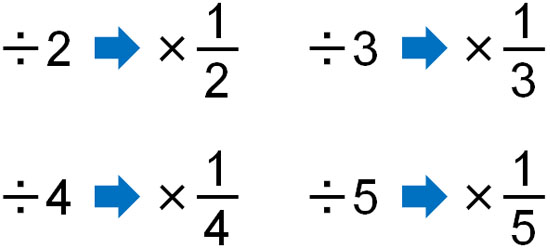
In elementary school math, we use division. However, after studying positive and negative numbers, it is important to consider that division is basically never used in the four arithmetic operations. All people change division into multiplying fractions in their calculations.
Therefore, for the previous calculation, we should convert and calculate as follows.
- $6\textcolor{red}{÷2}×3=6\textcolor{red}{×\displaystyle\frac{1}{2}}×3=9$
With multiplication, the answer is the same whether you calculate from the left or the right. Even if it is not divisible, we can use fractions to get the answer. Even the division of decimals is easy to calculate if you convert it into multiplying fractions.
The division is not useful and is rarely used in math calculations. So be sure to convert it to multiplying fractions.
Exercise: Four Arithmetic Operations of Positive and Negative Number
Q1: Do the following calculation.
- $-5-4×-3$
- $3+8÷(-2)$
- $-2^3×(5-3^2)$
A1: Answers.
To review, the four rules of arithmetic for positive and negative numbers must be performed in the following order.
- Calculating powers.
- Calculate inside parentheses.
- Do multiplication and division.
- Do addition and subtraction.
Calculated in this order, we get the following.
(a)
$-5-\textcolor{red}{4×-3}$
$=-5-\textcolor{red}{(-12)}$
$=-5+12$
$=7$
(b)
$3+\textcolor{red}{8÷(-2)}$
$=3+\textcolor{red}{(-4)}$
$=3-4$
$=-1$
(c)
$-\textcolor{red}{2^3}×(5-\textcolor{blue}{3^2})$
$=-\textcolor{red}{8}×(5-\textcolor{blue}{9})$
$=-8×(-4)$
$=32$
Q2: Do the following calculation.
- $3^2-(-3)^2×(-2)^2$
- $6÷\displaystyle\frac{3}{2}×3+\displaystyle\frac{1}{2}$
- $(7-3^2)×2^2-(-6)÷(-3)^2$
A2: Answers.
The calculations are a little more complicated than the previous ones. Also, there are some divisions that are not divisible. For division, as mentioned earlier, you need to convert them to multiplying fractions.
Then you get the following.
(a)
$3^2-(-3)^2×(-2)^2$
$=9-9×4$
$=9-36$
$=-27$
(b)
$6\textcolor{red}{÷\displaystyle\frac{3}{2}}×3+\displaystyle\frac{1}{2}$
$=6\textcolor{red}{×\displaystyle\frac{2}{3}}×3+\displaystyle\frac{1}{2}$
$=12+\displaystyle\frac{1}{2}$
$=\displaystyle\frac{24}{2}+\displaystyle\frac{1}{2}$
$=\displaystyle\frac{25}{2}$
(c)
$\textcolor{red}{(7-3^2)×2^2}-\textcolor{blue}{(-6)÷(-3)^2}$
$=\textcolor{red}{(7- 9)×4}-\textcolor{blue}{(-6)÷9}$
$=\textcolor{red}{-2×4}-\textcolor{blue}{(-6)×\displaystyle\frac{1}{9}}$
$=-8-(-\displaystyle\frac{6}{9})$
$=-8-(-\displaystyle\frac{2}{3})$
$=\textcolor{red}{-8}+\displaystyle\frac{2}{3}$
$=\textcolor{red}{-\displaystyle\frac{24}{3}}+\displaystyle\frac{2}{3}$
$=-\displaystyle\frac{22}{3}$
Four Rules of Arithmetic for Addition, Subtraction, Multiplication and Division
When learning positive and negative numbers, four rules of arithmetic is more complicated. Not only do we have to think about what the signs will be, but we also have to learn rules of four arithmetic operations because we use powers and parentheses to calculate them.
We have explained how to calculate four arithmetic operations, including why there are such math rules. There is a correct order for solving problems in mathematics, so be sure to calculate in the correct order.
Also, for division, you can convert it to multiplying fractions. The division is rarely used. In fact, when learning more advanced mathematics in high school, no one uses division. Instead, we use multiplying fractions to calculate. Therefore, always convert division to multiplication.
There are rules and tips for solving math problems. Try to understand the rules of mathematics, including the reasons, to solve the problems.