小学算数では「場合の数」を学びます。ある事柄について、何通りの方法があるのかかぞえるのが場合の数です。
場合の数には、「並べかた」と「組み合わせ」があります。つまり、2つのがいねんを理解しなければいけません。また答えをだすため、樹形図を利用することによって一つずつかぞえる必要があります。
並べかたや組み合わせは、高校数学など後になって確率や統計を学ぶときに必須となるがいねんです。そのためプログラミングや工場、医療など多くの分野で利用されています。宝くじも確率の分野といえます。場合の数を学ぶことによって、これらの分野の仕組みがわかるようになります。
そこで、何通りのパターンがあるのかかぞえられるようになりましょう。ここでは、並べかたと組み合わせの基本を解説していきます。
もくじ
何通り起こるのかかぞえるのが場合の数
場合の数では、ある事柄が何通り起こるのかをかぞえます。例えば、以下のように3枚のカードがあります。ここから一枚のカードを選ぶとき、何通りの方法があるでしょうか。

カードは3枚であるため、当然ながら3通りのパターンがあります。いずれにしても、このように何通りの方法があるのか考えるのが場合の数です。
ただ、場合の数には「並べかた」と「組み合わせ」の2種類があります。そのため、それぞれのやり方を理解するようにしましょう。
順番を考えるのが並べかた
並べかたとは何でしょうか。並べかたでは、順番を考えます。つまり、どのような順番で並ぶのかが重要になります。例えば、以下のような場面では順番を区別します。
- カードを左から順に並べる
- リレーの走り順を決める
- 旅行で行き先の順番を決める
このように、並べかたでは必ず順番を決めます。一番目や二番目、三番目を決めるのが並べかたであると理解しましょう。
樹形図を利用し、何通りあるのかかぞえる
それでは、どのようにして並べかたで答えをだせばいいのでしょうか。方法としては、樹形図を利用しましょう。木の枝のように、分かれていくのが樹形図です。例えば、以下の答えは何でしょうか。
- 3人のうち、リレーの第一走者と第二走者を決めます。何通りの方法がありますか?

リレー走者の順番を決めることになるため、並べかたの問題になります。樹形図を利用するとき、以下のように一番目を記載しましょう。

次に、第二走者を決めます。第一走者が決まっているため、第二走者の候補は2人です。そのため、以下のように二番目を記載することができます。
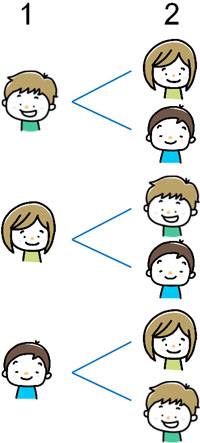
このように樹形図を利用することによって、何通りの方法があるのかかぞえることができます。樹形図を使えば、重複や記載もれなくすべてのパターンを書き出すことができます。そのため計算ミスを少なくできます。
明確に区別できる場合は並べかた
なお並べかたには複数のパターンがあります。必ずしも、順番を決めるとは限りません。並べかたというのは、明確に区別できるように並べることを意味します。例えば、以下の答えは何でしょうか。
- A、B、C、D、Eの5人から、リーダーと副リーダーを決めます。何通りの方法がありますか?
リーダーと副リーダーは役割が違います。そのため明確に分けることができます。また、この場合は「リーダーと副リーダーを順番に並べる」と言い換えることもできます。問題文に「順番」という言葉は出てこないものの、この問題では何通りの順番があるのかを考えるようにしなければいけません。
樹形図を利用すると、以下のようになります。
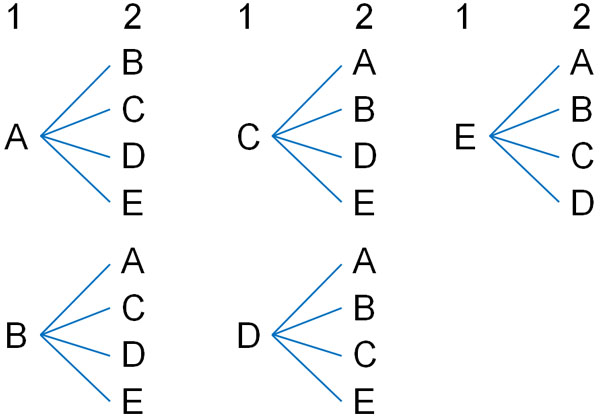
一番目(リーダー)にはA~Eの5通りがあります。その後、二番目(副リーダー)を決めます。リーダーはすでに決まっているため、副リーダーは4通りの方法があります。これをすべて樹形図に記すことによって、上図を作ることができます。
樹形図を確認すると、全部で20通りの方法があります。そのため、答えは20通りになります。
かけ算を利用して素早く問題を解く
参考までに、並べかたの問題はかけ算を利用することによって素早く解くことができます。樹形図を利用することによって答えをだすことができるものの、樹形図を作るには時間がかかります。そのため樹形図を描くのに慣れ、並べかたの意味を理解したのであれば、かけ算を利用して計算してもいいです。
例えば、以下の問題の答えは何でしょうか。
- 1、2、3、4の数字を使い、3ケタの数を作ります。何通りの方法がありますか?

3ケタの数を作るというのは、一番目、二番目、三番目と数を順番に並べることと意味が同じです。順番が重要になるため、並べかたの問題です。樹形図にすると以下のようになります。
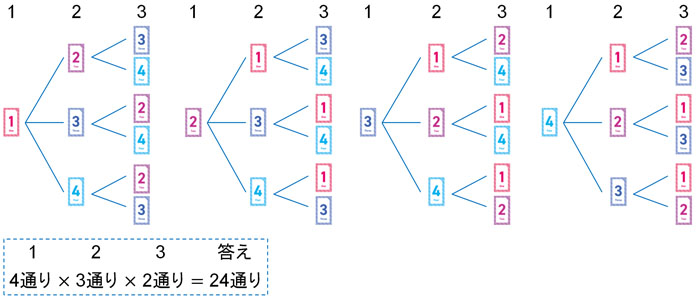
樹形図を描くことによって、答えは24通りであるとわかります。このとき一番目や二番目、三番目に配置できるカードについて、何通りの方法があるのか考えるようにしましょう。
4つの数字があるため、一番目に配置できる数字は4通りあります。また、一番目で数字を一つ利用しているため、二番目に配置できる数字は3通りあります。同じように考えると、三番目に配置できる数字は2通りあります。
そのため樹形図を描かなくても、並べかたでは以下のようにかけ算を利用して計算することができます。
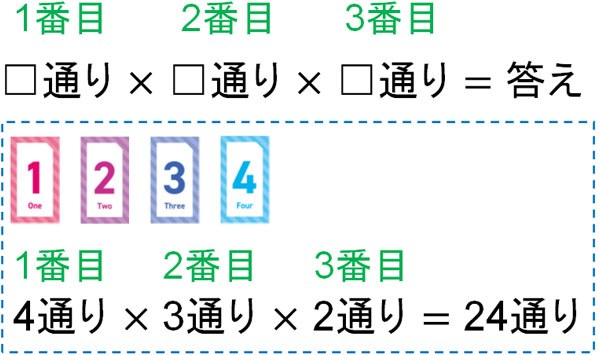
樹形図を利用すれば、答えをだすことができます。ただ今回の問題のように、候補が多いと24通りの方法を記す必要があり、樹形図を描くのに時間がかかります。そこで並べかたの性質を理解し、かけ算を利用すれば、樹形図なしに問題を解くことができます。
組み合わせでは、順番を区別しない
次に理解しなければいけないがいねんが組み合わせです。組み合わせでは、先ほど説明したかけ算を利用することはできません。必ず樹形図を利用して問題を解くようにしましょう。
まず、組み合わせとは何でしょうか。並べかたとは何が違うのでしょうか。組み合わせとは、順番を区別せずに選ぶ方法です。並べかたでは順番が重要です。一方、組み合わせでは順番を区別しないのです。
例えば、以下のような違いになります。
・リレー走者を選ぶ
- 並べかた:5人から第一走者と第二走者を選ぶ
- 組み合わせ:5人から二人の走者を選ぶ
並べかたでは、第一走者と第二走者のように順番を決めます。一方で組み合わせでは、二人を選びます。どちらが第一走者なのかはわかりません。
・クラスの代表を選ぶ
- 並べかた:8人からリーダーと副リーダーを決める
- 組み合わせ:8人から二人のリーダーを決める
並べかたでは、リーダーと副リーダーを明確に区別して選びます。一方で組み合わせでは、二人を選びます。二人ともリーダーであり、区別をしたり順番を決めたりすることはできません。
・カードを選ぶ
- 並べかた:1~6の数字が書かれているカードを使い、3ケタの数字を作る
- 組み合わせ:1~6の数字が書かれているカードから、3枚を選ぶ
並べかたでは、3枚のカードを選んだあとに左から順に並べます。並べる順番によって、3ケタの数字が異なります。一方で組み合わせでは3枚のカードを選ぶものの、順番は関係ありません。3枚のカードを選ぶとき、「1、4、5」であっても「4、1、5」であっても同じ種類とみなします。
このように、順番を考えないのが組み合わせです。並べかたに比べて、組み合わせは考え方がむずかしくなります。
樹形図を利用した後、同じものを排除する
それでは、どのように組み合わせの問題を解けばいいのでしょうか。先ほど説明した通り、組み合わせではかけ算を利用してはいけません。樹形図を利用して問題を解くようにしましょう。
例えば、以下の問題の答えは何でしょうか。
- 4枚のカードから2枚を取るとき、何通りの方法があるでしょうか。

カードを選んだあと、新たな数字を作ったり、左から順に並べたりしません。カードの順番を区別しないため、組み合わせの問題になります。そこで、並べかたと同じように以下のような樹形図を作りましょう。
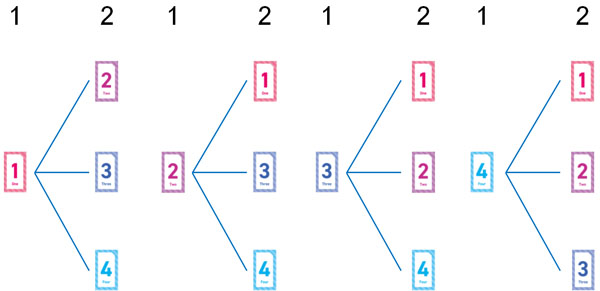
ただ樹形図では、前述の通り順番を考えます。このままでは、順番を含む答えがでてしまいます。そこで組み合わせの答えをだすとき、同じものを排除しましょう。
順番を無視する場合、例えば「1、2」と「2、1」は同じです。また、「1、4」と「4、1」は同じです。そこで同じものを排除すると、以下のようになります。
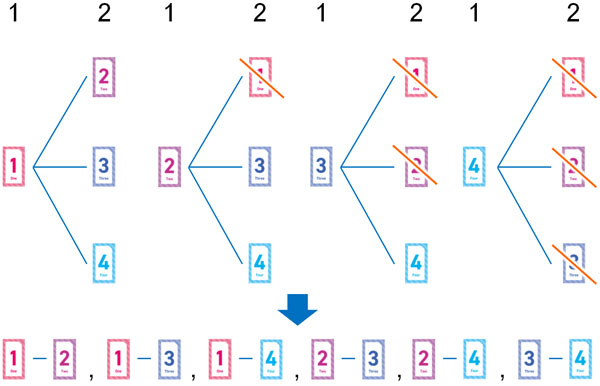
同じものを排除した後、何通りの組み合わせがあるのかかぞえると、全部で6通りになります。こうして、樹形図を利用して組み合わせの問題を解きます。
表を利用して答えをだす:スポーツでのリーグ戦
なお組み合わせの問題を解くとき、表を利用する方法もあります。スポーツでリーグ戦をするときに利用する、以下のような表を使うのです。
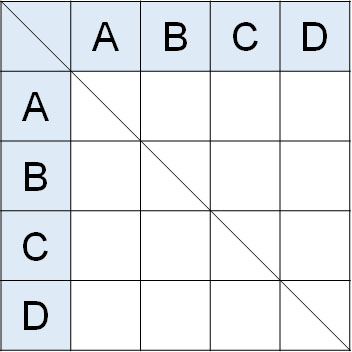
もちろん、この表はスポーツでのリーグ戦のみに利用できるわけではありません。さまざまな組み合わせの問題を解くときに利用できます。それでは、以下の問題を解いてみましょう。
- A、B、C、D、Eの五人から、二人の代表者を選びます。何通りの方法がありますか?
二人のリーダーを区別することはできません。そのため、組み合わせの問題になります。そこで表を作り、右上半分にチェック(✓)を加えましょう。
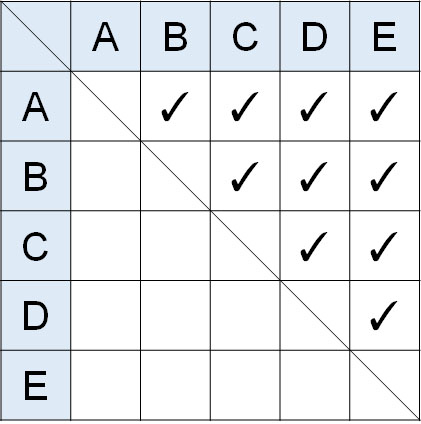
チェックの数が答えになります。つまり、組み合わせの答えは10通りです。
リーグ戦の表を利用するとき、上図の左下半分にチェックを入れてはいけません。理由としてはA-BとB-Aは同じだからです。組み合わせでは順番を区別しません。そのため表のすべてにチェックを入れると、間違った答えがでてしまいます。
・表を利用できる場面は少ない
なお注意点としては、表を利用して組み合わせの問題を解く場合、2組を選ぶときのみ利用できることです。例えば8枚のカードのうち、2枚を選ぶときは表を利用することができます。一方、8枚のカードから3枚を選ぶとき、表を利用して問題を解くことができません。
スポーツでのリーグ戦では、2つのチームが競うことになります。同時に3組が競うことはありません。表を利用して組み合わせの問題を解くことはできるものの、利用できるケースは少ないです。そのため、組み合わせの問題を解くときは樹形図を主に利用しましょう。
小学算数の組み合わせは高校数学より難しい
参考までに、小学算数の組み合わせは答えをだすのが難しいです。樹形図を利用し、そのあとに同じものを排除する必要があり、ミスがひんぱんに起こるのです。並べかたのように、かけ算をすることで簡単に答えをだす方法はなく、樹形図(または表)を利用して一つずつかぞえなければいけません。
実際のところ、小学算数で学ぶ組み合わせは高校数学よりもむずかしいです。高校数学の場合、公式を学びます。組み合わせの問題を解くとき、高校数学では公式を利用することによって簡単に答えをだすことができます。
一方で小学算数では公式を学ばず、樹形図を利用して問題を解かなければいけません。そのためミスが起こりやすいのです。
要は、樹形図や表を利用して組み合わせの問題を解くとき、ミスをしたとしても大きな問題ではありません。将来は公式を学ぶことになるため、計算ミスする確率は大幅に少なくなります。実際のところ樹形図を利用して組み合わせの問題を解くのは面倒であり、むずかしいやり方であることを理解しましょう。
並べかたと組み合わせの問題を解く
何通りの方法があるのか、かぞえるのが場合の数です。場合の数には、「並べかた」と「組み合わせ」の2種類があります。
並べかたと組み合わせはがいねんが異なります。並べかたでは順番が重要になります。そのため樹形図を利用することで問題を解くことができますし、かけ算を利用して答えをだすこともできます。
それに対して、組み合わせでは順番を考えません。順番を区別せずに選ぶのが組み合わせです。そのため樹形図(または表)を利用するとき、同じものを排除しましょう。そうすると、組み合わせのパターンをかぞえることができます。
どのようなときに「並べかた」を利用し、どのようなときに「組み合わせ」を利用するのか区別しましょう。そうして樹形図を利用し、答えをだすといいです。






