分数の計算でひんぱんに行うことになるのが約分と通分です。答えがでたとしても、約分をしなければ正しい答えではありません。また通分をしなければ、分数のたし算や引き算をすることができません。
約分と通分は分数の計算で必ず理解しなければいけません。それでは、約分とは何でしょうか。また、通分はどのようにすればいいのでしょうか。
約分や通分をするためには、分数の性質をまず学ばなければいけません。そうすれば、公約数や公倍数の知識を使うことで約分や通分ができるようになります。
分数で必ず利用するのが約分と通分です。どのように約分や通分をすればいいのか解説していきます。
もくじ
約分のやり方:同じ数でわっても答えは同じ
まず、約分とは何でしょうか。約分とは、分数の数字を小さくする作業と理解しましょう。たとえば、\(\displaystyle\frac{2}{3}\)と\(\displaystyle\frac{14}{21}\)では、どちらを認識しやすいでしょうか。
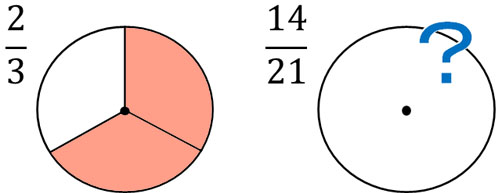
大きい数字は理解しにくいです。これが、分数で数字を小さくしなければいけない理由です。
それでは、どのようにすれば約分によって分数の数を小さくできるのでしょうか。やり方としては、分子と分母を同じ数でわりましょう。分数には、「同じ数で分子と分母をわったとしても、答えが変わらない」という性質があります。たとえば、以下のようになります。
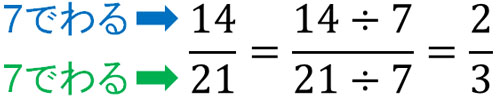
このようにして、\(\displaystyle\frac{14}{21}=\displaystyle\frac{2}{3}\)と表すことができます。
それでは、なぜ分子と分母に対して同じ数でわっても答えが同じになるのでしょうか。分数というのは、ものを分けた後、いくつ含まれているのかを表す数字です。
たとえば、\(\displaystyle\frac{1}{3}\)と\(\displaystyle\frac{2}{6}\)を比べてみましょう。\(\displaystyle\frac{2}{6}=\displaystyle\frac{2÷\color{red}{2}}{6÷\color{red}{2}}=\displaystyle\frac{1}{3}\)となり、2つの分数は同じです。また\(\displaystyle\frac{1}{3}\)とは、1を3等分することを意味します。一方、\(\displaystyle\frac{2}{6}\)は1を6等分したあと、\(\displaystyle\frac{1}{6}\)を2つあつめることを意味します。そのため、図にすると以下のようになります。
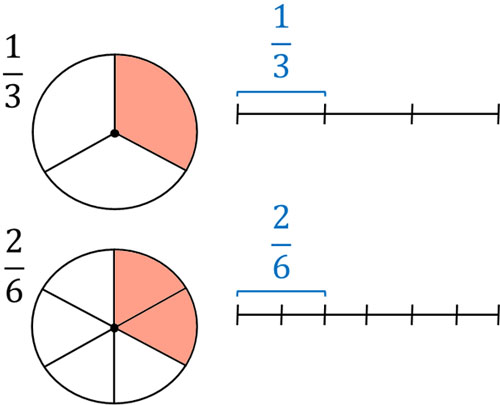
このように、図にすると\(\displaystyle\frac{1}{3}\)と\(\displaystyle\frac{2}{6}\)は同じ数字であると分かります。これが分数の性質であり、分子と分母に対して同じ数でわっても答えは変わらないのです。
公約数を見つけ、わることで約分する
それでは、どのようにして約分をすればいいのでしょうか。約分をする方法としては、公約数を見つけるようにしましょう。たとえば、\(\displaystyle\frac{12}{18}\)はどのように約分すればいいのでしょうか。分子と分母について、共通する約数を見つけるようにしましょう。
12と18は偶数なので、2でわることができます。そのため、以下のように約分できます。
- \(\displaystyle\frac{12}{18}=\displaystyle\frac{12÷2}{18÷2}=\displaystyle\frac{6}{9}\)
ただ、この分数はさらに約分できます。6と9には3という公約数があるため、分子と分母を3でわりましょう。
- \(\displaystyle\frac{6}{9}=\displaystyle\frac{6÷3}{9÷3}=\displaystyle\frac{2}{3}\)
こうして、\(\displaystyle\frac{12}{18}\)を\(\displaystyle\frac{2}{3}\)へ約分することができました。
約分をするとき、最大公約数を利用すれば効率的に約分できます。先ほどの\(\displaystyle\frac{12}{18}\)であれば、12と18の最大公約数は6です。そのため6でわれば、一回のわり算によって約分が完了します。
しかし数字が大きい場合、最大公約数を見つけるのはむずかしいです。そのため2や3などの小さい数を利用し、わり算できるかどうか確認するのが一般的な方法です。計算ミスを防ぐため、最大公約数ではなく、小さい数字を利用して約分するのはすぐれた方法です。
分子と分母に同じ数をかけても答えは同じ
ここまで、分子と分母を同じ数でわって同じ答えになることを解説しました。これは、逆もいえます。つまり、分子と分母に同じ数をかけても答えは同じです。たとえば、以下はすべて同じ数です。
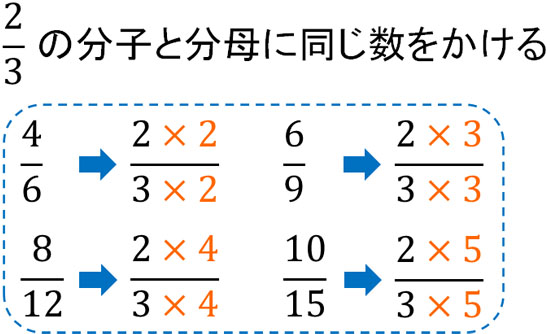
分数では、分子と分母に対して同じ数でわっても数字は同じです。同様に、分子と分母に対して同じ数をかけても数字は同じです。この性質を理解しましょう。
またこの性質を理解すれば、かんたんに整数を分数に変換できるようになります。たとえば3を\(\displaystyle\frac{☐}{4}\)という形の分数にする場合、整数である3と分母である4のかけ算をします。以下のようにして、整数を分数に変えることができます。
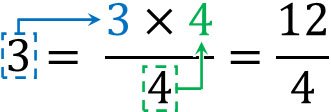
なぜ、このようにすることができるのでしょうか。この理由として、分子と分母に同じ数をかけても同じ数になるからです。
まず、3を分数に変換すると\(\displaystyle\frac{3}{1}\)になります。分母が1の場合、通常は分母を省きます。ただ、このように整数を分数に変えることができることを理解しましょう。その後、分子と分母に対して同じ数をかけます。すると、以下のようになります。
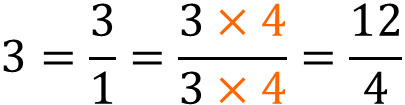
整数を分数に変えるとき、「整数と分母のかけ算をする」という説明では理解がむずかしいです。一方で約分を学び、分子と分母に同じ数をかけても同じ答えになることを理解すれば、整数を分数に変える方法を理解しやすくなります。
通分することで同じ分母にする
なお約分ができるようになったら、次は通分を行えるようにしましょう。約分では公約数を利用して数を小さくします。一方で通分では、公倍数を利用することで数を大きくします。
先に述べた通り、分子と分母に同じ数をかけても、同じ数になります。通分ではこの性質を利用します。
通分とは、分母を同じにすることを意味します。たとえば、\(\displaystyle\frac{1}{2}\)と\(\displaystyle\frac{1}{3}\)について、どのように分母をそろえればいいでしょうか。\(\displaystyle\frac{1}{2}\)と\(\displaystyle\frac{1}{3}\)について、それぞれ以下のような分数に変えてみましょう。
- \(\displaystyle\frac{1}{2}=\displaystyle\frac{1×3}{2×3}=\displaystyle\frac{3}{6}\)
- \(\displaystyle\frac{1}{3}=\displaystyle\frac{1×2}{3×2}=\displaystyle\frac{2}{6}\)
このように、\(\displaystyle\frac{1}{2}\)の分子と分母に3をかけることによって\(\displaystyle\frac{3}{6}\)となります。また、\(\displaystyle\frac{1}{3}\)の分子と分母に2をかけることによって\(\displaystyle\frac{2}{6}\)となります。
こうして、分母をそろえることができました。これが通分です。
たし算や引き算は同じ分母で可能
なぜ通分をすることによって分母をそろえなければいけないのでしょうか。この理由として、分母が同じでなければ、分数のたし算や引き算をすることができないからです。
たとえば、\(\displaystyle\frac{3}{4}\)は\(\displaystyle\frac{1}{4}\)を3つあつめたものです。また、\(\displaystyle\frac{2}{4}\)は\(\displaystyle\frac{1}{4}\)を2つあつめたものです。そのため、\(\displaystyle\frac{3}{4}+\displaystyle\frac{2}{4}=\displaystyle\frac{5}{4}\)になります。
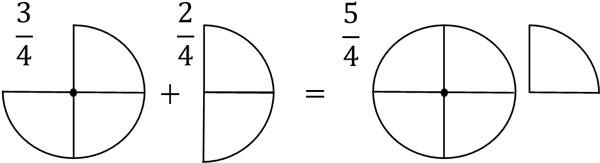
分数のたし算と引き算では、必ず分母が同じでなければいけません。以下のように、分母が違う場合は明確な答えを出すことができません。
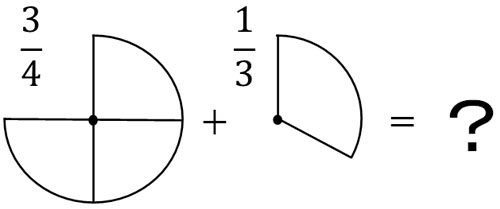
そこで、分母を同じにするために通分しましょう。通分をすれば、分母が同じになるので足し算や引き算をすることができます。
たとえば、\(\displaystyle\frac{3}{4}+\displaystyle\frac{1}{2}\)の計算をすることはできません。一方、\(\displaystyle\frac{1}{2}=\displaystyle\frac{2}{4}\)にすることで、式を以下のように変えれば計算することができます。
- \(\displaystyle\frac{3}{4}+\displaystyle\frac{1}{2}=\displaystyle\frac{3}{4}+\color{red}{\displaystyle\frac{2}{4}}=\displaystyle\frac{5}{4}\)
分母が違う場合、たし算や引き算ができるようにするためには、通分をしなければいけません。
最小公倍数を見つけ、分子と分母にかけ算をする
それでは、どのようにして通分をすればいいのでしょうか。共通の分母にするためには、最小公倍数を利用するようにしましょう。
たとえば、\(\displaystyle\frac{1}{4}\)と\(\displaystyle\frac{1}{6}\)の通分はどのようにすればいいでしょうか。通分をするとき、分母に着目しましょう。2つの分数について、分母は4と6です。そこで、4と6の最小公倍数を見つけるようにしましょう。それぞれの倍数は以下のようになります。
- 4の倍数:4、8、12、16、20、24、28、32、36、40……
- 6の倍数:6、12、18、24、30、36、42……
共通する倍数として12や24、36があります。これら公倍数の中で、最小公倍数を通分で利用しましょう。4と6の最小公倍数は12です。そこで、分母の数字が12になるように分数を変えましょう。以下のようになります。
- \(\displaystyle\frac{1}{4}=\displaystyle\frac{3}{12}\)
- \(\displaystyle\frac{1}{6}=\displaystyle\frac{2}{12}\)
このように、\(\displaystyle\frac{1}{4}\)を\(\displaystyle\frac{3}{12}\)に変えます。また、\(\displaystyle\frac{1}{6}\)を\(\displaystyle\frac{2}{12}\)に変えます。これによって分母が同じになるため、たし算または引き算をすることができます。
なお通分をするとき、一般的には分母を最小公倍数にします。ただ、場合によっては最小公倍数を見つけられないこともあります。その場合、必ずしも分母を最小公倍数にする必要はありません。分母が同じであれば分数のたし算や引き算をすることができるため、通分では他の公倍数を利用して通分してもいいです。
たとえば\(\displaystyle\frac{1}{4}\)と\(\displaystyle\frac{1}{6}\)の通分をするとき、以下のようにしてもいいです。
- \(\displaystyle\frac{1}{4}=\displaystyle\frac{6}{24}\)
- \(\displaystyle\frac{1}{6}=\displaystyle\frac{4}{24}\)
先ほど、分母を最小公倍数である12にしました。一方、今回は分母を他の公倍数である24にしました。この場合であっても分母が同じであるため、たし算や引き算をすることができます。
公倍数をみつける最もかんたんな方法としては、2つの分母をかける方法があります。たとえば\(\displaystyle\frac{1}{4}\)と\(\displaystyle\frac{1}{6}\)の分母は4と6です。そこで\(4×6=24\)をすれば、公倍数として24をみつけることができます。この方法では、最小公倍数である12をみつけるよりもかんたんです。
通分で重要なのは、分母をそろえることです。最小公倍数を利用するのが最も一般的であるものの、他の公倍数を利用して通分しても問題ありません。
通分によって分数の大小をみわける
通分ができるようになれば、分数を比較するとき、数字の大小を見分けられるようになります。たとえば、以下の数字はどちらのほうが大きいでしょうか。
- \(\displaystyle\frac{2}{5}\)、\(\displaystyle\frac{3}{8}\)
通分を習っていない場合、この問題を解くことはできません。一方、通分のやり方を理解していれば、どちらの数字が大きいのか分かるようになります。この問題を解くためには、分数を通分しましょう。つまり、分母をそろえるのです。分母が同じであれば、分子の数を比較することで分数の大小を判断できます。
分母の数を確認すると5と8です。5と8の最小公倍数は40です。そこで2つの分数について、分母を40にしましょう。以下のようになります。
- \(\displaystyle\frac{2}{5}=\displaystyle\frac{16}{40}\)
- \(\displaystyle\frac{3}{8}=\displaystyle\frac{15}{40}\)
このように、\(\displaystyle\frac{2}{5}=\displaystyle\frac{16}{40}\)であり、\(\displaystyle\frac{3}{8}=\displaystyle\frac{15}{40}\)とわかります。また分母が同じなので、分子を比較することで分数の大小がわかります。
\(\displaystyle\frac{16}{40}\)と\(\displaystyle\frac{15}{40}\)を比べると、\(\displaystyle\frac{16}{40}\)のほうが数字は大きいです。また、\(\displaystyle\frac{2}{5}=\displaystyle\frac{16}{40}\)です。そのため、\(\displaystyle\frac{3}{8}\)よりも\(\displaystyle\frac{2}{5}\)のほうが大きい数字であると分かります。
分数同士を比べるとき、分母が同じであれば大小の比較をすることができます。また、たし算や引き算をすることもできます。そのため分数の計算では通分が重要になります。
最大公約数と最小公倍数を使い、約分と通分をする
小学校の算数で学ぶ重要な内容が分数です。分数では約分や通分をする場面がいくつもあります。そこで、どのようにすれば約分や通分ができるのか理解しましょう。
約分で重要なのが公約数です。分子と分母に対して、同じ数でわっても同じ分数になります。そこで分子と分母の数について最大公約数を見つけ、わり算をしましょう。また最大公約数を見つけるのが難しい場合、2や3など小さい数字を利用してわり算をするといいです。
一方、分数のたし算や引き算では分母をそろえなければいけないことがひんぱんにあります。その場合、通分をしましょう。分子と分母について同じ数をかける場合、同じ数字になります。この性質を利用して、分数の数字を変えましょう。また最小公倍数を見つけられない場合、他の公倍数を利用して分母を同じにしてもいいです。
分数で約分と通分は必須の知識です。分数の概念を学んだあと、約分と通分のやり方を理解するようにしましょう。