1よりも小さい数を表せる方法に分数と小数があります。両方ともひんぱんに算数の計算問題でだされます。
重要なのは、分数は小数に変えることができるということです。また、小数を分数に変えることもできます。そこで、どのように計算すればいいのか理解しましょう。
また算数では、一般的に小数ではなく分数を利用して計算しましょう。実際、分数と小数が混じっている計算問題では、すべての数を分数に変えます。また小数のみを含む計算問題であっても、答えを分数でだすことがひんぱんにあります。
分数ではあらゆる数字を表現できます。そこで、分数と小数の関係性を理解しましょう。
もくじ
分数を小数に直す方法
まず、分数を小数に直す方法から学びましょう。分数はわり算と意味が同じです。そこで分数をわり算の式に変えて計算すれば、分数を小数に直すことができます。例えば、\(\displaystyle\frac{1}{4}\)を小数に直すとどのような数字になるでしょうか。
そこで、分数をわり算に変えましょう。以下のようになります。
- \(\displaystyle\frac{1}{4}=1÷4=0.25\)
このように、わり算をすることで分数を小数に変換できます。
この計算方法は帯分数でも同様であり、帯分数をわり算の式に変えましょう。そこで帯分数を仮分数に変え、わり算の式を作りましょう。
例えば、\(2\displaystyle\frac{1}{2}\)はどのように仮分数へ変えればいいでしょうか。\(2\displaystyle\frac{1}{2}\)を仮分数に直す場合、以下のようになります。
- \(2\displaystyle\frac{1}{2}=\displaystyle\frac{4}{2}+\displaystyle\frac{1}{2}=\displaystyle\frac{5}{2}\)
次に\(\displaystyle\frac{5}{2}\)を小数に変えましょう。以下のようになります。
- \(\displaystyle\frac{5}{2}=5÷2=2.5\)
帯分数の計算では、ほかにもやり方があります。ただ帯分数は中学数学や高校数学など高度な数学では使わないため、仮分数を利用して計算する方法に慣れましょう。
分数を小数に変換できないことは多い
なお分数を小数に変えようとしても、小数に変換できないことは多いです。例えば、\(\displaystyle\frac{1}{3}\)を小数にするにはどうすればいいでしょうか。実は、\(\displaystyle\frac{1}{3}\)を小数にすることはできません。
\(\displaystyle\frac{1}{3}=1÷3\)です。そこでこの計算をすると、以下のようになります。
- \(1÷3=0.3333333333…\)
このように、数字が永遠に続きます。わり算をするとき、わりきれない場合があります。この場合、分数を小数に変えることはできません。
重要なのは、わりきれない計算であったとしても、分数であれば答えを出せるという事実です。小数では答えをだすことができなかったとしても、分数であれば答えをだすことができます。そのため、算数では小数よりも分数のほうが多く利用されます。
小数を分数に変えるやり方
次に、小数を分数に変える方法を理解しましょう。前述の通り、分数を小数に変える場合、小数に変換できないことがあります。一方、小数から分数への変換は必ず行うことができます。
小数を分数に変えるとき、以下の関係性を覚えましょう。
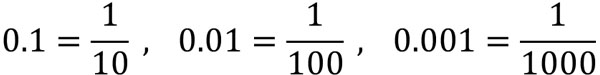
事実、\(\displaystyle\frac{1}{10}=1÷10=0.1\)です。また、\(\displaystyle\frac{1}{100}=1÷100=0.01\)となります。そのため、例えば0.2は\(\displaystyle\frac{2}{10}\)です。
小数点を右にいくつ移動できるのかを確認すれば、分数を作ることができます。例えば、0.1では小数点を右に1つ移動できます。また、0.01では小数点を右に2つ移動できます。0.001の場合、小数点を右に3つ移動できます。
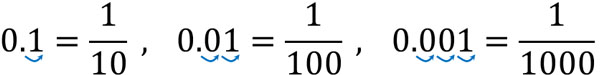
その後、小数点を移動させた数と同じだけ、ゼロを分母に記しましょう。さらに、小数点を省いた数字を分子に記しましょう。
例えば、0.152を分数に直しましょう。0.152を確認すると、小数点を右に3つ移動させることができます。そのため、分母に3つのゼロを書きましょう。つまり、分母は1000です。また、小数点を省いた数字を分子に記すため、152を分子に記します。
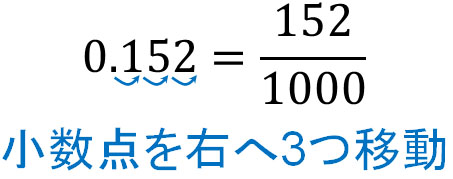
なお、約分を忘れずに行いましょう。以下のようになります。
\(\displaystyle\frac{152}{1000}\)
\(=\displaystyle\frac{152÷2}{1000÷2}\)
\(=\displaystyle\frac{76}{500}\)
\(=\displaystyle\frac{76÷2}{500÷2}\)
\(=\displaystyle\frac{38}{250}\)
\(=\displaystyle\frac{38÷2}{250÷2}\)
\(=\displaystyle\frac{19}{125}\)
こうして、\(\displaystyle\frac{19}{125}\)が答えになります。大きい数字の約分をするとき、最大公約数をみつけるのは難しいです。そこで2や3など小さい数字を利用して、分子と分母を同じ数でわれなくなるまで約分をするようにしましょう。
一方、1.25はどのようにして分数へ変えればいいでしょうか。
先ほどと同じように、小数点をいくつ右に移動できるか確認しましょう。そうすると、小数点を右へ2つ移動できることが分かります。また、小数点を省いた数字を分子に記しましょう。以下のようになります。
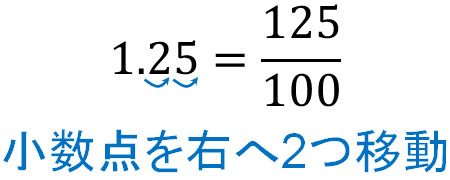
こうして、\(1.25=\displaystyle\frac{125}{100}\)になります。また約分をすると以下のようになります。
\(\displaystyle\frac{125}{100}\)
\(=\displaystyle\frac{125÷5}{100÷5}\)
\(=\displaystyle\frac{25}{20}\)
\(=\displaystyle\frac{25÷5}{20÷5}\)
\(=\displaystyle\frac{5}{4}\)
こうして約分まですると、答えをだすことができます。
小数と分数が混じった計算問題:すべての小数を分数にする
なお小数と分数について学んだあと、小数と分数が混じった計算問題をすることがあります。この問題はどのように解けばいいのでしょうか。
性質が異なる数字を計算する場合、性質をそろえると計算しやすいです。そこで、小数または分数へ変えるようにしましょう。
なお一般的には、小数と分数が混じっている計算問題では、すべて分数の式に変えます。前述の通り、分数を小数に変えられないケースはひんぱんにあります。一方、小数は必ず分数に変えることができます。そのため、小数ではなくすべて分数に変えるのです。
例えば、小数と分数が混じった以下の計算問題をどのようにして解けばいいでしょうか。
- \(5.2÷\displaystyle\frac{3}{2}×\displaystyle\frac{5}{4}\)
まず、小数を分数に変えましょう。5.2を分数にする場合、\(5.2=\displaystyle\frac{52}{10}\)となります。そのため、計算式は以下のようになります。
- \(\displaystyle\frac{52}{10}÷\displaystyle\frac{3}{2}×\displaystyle\frac{5}{4}\)
また、分数のわり算は必ず分数のかけ算にしなければいけません。そこで逆数を利用し、以下のようにかけ算の式にしましょう。
- \(\displaystyle\frac{52}{10}\color{red}{×\displaystyle\frac{2}{3}}×\displaystyle\frac{5}{4}\)
これを計算しましょう。以下のようになります。
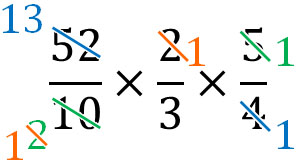
こうして、答えは\(\displaystyle\frac{13}{3}\)になります。約分をする順番はあなたのすきなようにすればいいです。いずれにしても、正しく小数を分数に変え、わり算をかけ算に変え、約分することができれば答えをだすことができます。
小数と小数の計算で答えを分数でだす
なお前述の通り、わり算ではわりきれない場合が多く、答えをだせないことがあります。その場合、分数で答えを出しましょう。
例えば、小数と小数のわり算をするとき、どのように答えをだせばいいでしょうか。わりきれない計算はすべて分数で答えをだしましょう。例えば、以下の計算をしましょう。
- \(7.2÷1.4\)
この計算をしたとしても、答えは5.14285…となり、永遠と数字が続いていきます。そこで、以下のように分数にしましょう。
- \(7.2÷1.4=\displaystyle\frac{7.2}{1.4}\)
その後、分母と分子を整数にします。分子と分母に対して、同じ数をかけても答えは同じです。そこで、分子と分母に10をかけましょう。
- \(\displaystyle\frac{7.2}{1.4}=\displaystyle\frac{7.2×10}{1.4×10}=\displaystyle\frac{72}{14}\)
次に約分をしましょう。
- \(\displaystyle\frac{72}{14}=\displaystyle\frac{72÷2}{14÷2}=\displaystyle\frac{36}{7}\)
こうして、答えをだすことができます。わりきれない計算であっても答えをだすことができるため、算数の計算では分数がひんぱんに利用されます。
分数と小数の関係を理解し、計算を行う
分数と小数は互いに変換できます。分数はわり算なので、わり算をすることで小数に変換できます。ただすべての小数は分数に変換できるものの、分数を小数に変換できないことがあります。わりきれない数であっても分数で表現できるものの、わりきれない場合は小数で表現できないからです。
そこで、どのように分数を小数に変えるのか理解しましょう。また小数を分数に変える場合、小数点の位置に着目しましょう。
なお、分数と小数が混じった計算問題を解かなければいけないことがあります。この場合、小数を分数に変えましょう。前述の通り、すべての小数を分数に変えることができるからです。
分数と小数の関係を理解しましょう。1より小さい数を表せる数字が分数と小数です。ただ性質が異なるため、どのように計算すればいいのか学びましょう。