小学算数で学ぶ内容に比例と反比例があります。一つの数字が増えることによって、もう一方の数字が同じ割合で増える場合、比例といいます。また数字が増えることによって、同じ割合で数字が減る場合を反比例といいます。
比例と反比例では、\(x\)と\(y\)を利用して式を作らなければいけません。つまり、文字を利用することになります。
またグラフを描けるようになることも重要です。式や表を確認して、比例と反比例のグラフを描けるようになりましょう。
比例と反比例の性質だけでなく、式やグラフの作り方を学びましょう。これによって、比例と反比例の問題を解けるようになります。
もくじ
比例とは何か:かけ算と表の関係で考える
まず、比例とは何なのでしょうか。比例の場合、\(x\)の値が増えることによって、同じ割合で\(y\)の値が増えます。
例えば横3cm、たて\(x\)cmの長方形の面積はいくらになるでしょうか。面積を\(y\)cm2とすると、以下の式を作ることができます。
- \(y=3x\)

\(x\)には、あらゆる数字が入ります。\(x\)は2かもしれませんし、\(x\)は100かもしれません。いずれにしても、\(x\)の値をあなたが自由に決めることができるのです。
それでは、\(x\)の値が1ずつ増えると\(y\)の値はどのように変化するでしょうか。実際に\(x\)に1や2、3などの数字を入れてみて、\(y\)の値をだしてみましょう。表にすると以下のようになります。
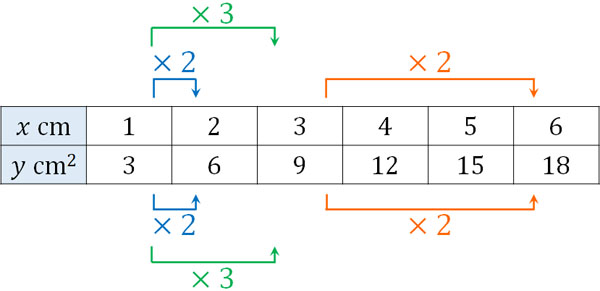
\(x\)の値が2倍になると、\(y\)の値は2倍になります。また\(x\)の値が3倍になると、\(y\)の値は3倍になります。このような関係が比例です。
比例は私たちの日常生活で広く利用されています。例えば、1つ10gのペンがあるとします。ペンの数が増えると、合計は同じ割合で重くなります。また、1つ100円のブドウがあるとします。ブドウを買う数が多くなると、お金の合計支払いは多くなります。そのため、比例を理解するのは重要です。
\(x\)と\(y\)で比例の式を作る
比例の性質を理解した後、\(x\)と\(y\)を利用して比例の式を作れるようにしましょう。比例の式では、例えば以下のようになります。
- \(y=2x\)
- \(y=5x\)
- \(y=20x\)
いずれにしても、\(x\)と何かの数字をかけ合わせることによって\(y\)の値を出します。そのため、比例の式は以下のようになります。
- \(y=\)決まった数\(×x\)
決まった数は定数とも呼ばれます。決まった数は2かもしれないし、30かもしれません。いずれにしても、何かの数が入ります。例えば1つ10gのペンについて、\(x\)個での合計の重さ(\(y\))を知りたい場合、以下の式になります。
- \(y=10×x\)
この場合、決まった数(定数)は10です。ペンの数(\(x\)の値)が一つ増えるごとに、合計の重さ(\(y\)の値)は10gずつ増えます。

このように、比例では必ず「\(y=\)決まった数\(×x\)」の式になることを理解しましょう。
決まった数(定数)の求め方
それでは、決まった数(定数)を見つけるにはどうすればいいのでしょうか。算数の問題によっては、\(x\)と\(y\)の値のみ与えられていることがあります。
中学数学では、\(y=\)決まった数\(×x\)ではなく、\(y=a×x\)という式で比例を学びます。\(a\)というのは、決まった数のことです。つまり、以下は同じ式です。
- \(y=\)決まった数\(×x\)
- \(y=a×x\)
ただ\(y=a×x\)ではわかりにくいため、決まった数を\(☐\)にしましょう。算数では、わからない数を\(☐\)にして計算することができます。つまり、比例の式は以下のようになります。
- \(y=☐×x\)
もし\(x\)と\(y\)の値がわかっている場合、\(x\)と\(y\)に値を入れることによって\(☐\)の値をだすことができます。例えば、比例関係にある以下の表について\(x\)と\(y\)の式で表してみましょう。

\(x\)が1のとき、\(y\)は6です。そこで\(y=☐×x\)に当てはめてみましょう。以下のようになります。
- \(6=☐×1\)
こうして、\(☐=6\)とわかります。\(☐\)は決まった数(定数)であり、この表は\(y=6x\)の式を表しています。
なお、先ほど\(x=1,y=6\)を利用して決まった数をだしました。比例の式では、\(x\)にどの値を入れても同じ割合で\(y\)の値が増えます。そのため、\(x\)と\(y\)についてほかの数字を利用しても決まった数を出すことができます。以下のようになります。
- \(x\)が2のとき、\(y\)は12:\(12=☐×2\)
- \(x\)が3のとき、\(y\)は18:\(18=☐×3\)
- \(x\)が4のとき、\(y\)は24:\(24=☐×4\)
- \(x\)が5のとき、\(y\)は30:\(30=☐×5\)
- \(x\)が6のとき、\(y\)は36:\(36=☐×6\)
これらの式について、すべて\(☐=6\)です。比例関係では、このように必ず決まった数(定数)は同じ値になります。例えば1つのペンの重さが10gのとき、合計の重さについて求める場合、比例の式を\(y=10×x\)ではなく、\(y=8×x\)にしてはいけません。決まった数は当然ながら10gであり、8gではないのです。
もちろん、問題文によって決まった数は異なります。1つのペンの重さが10gではなく、12gの場合であれば、合計の重さは\(y=12×x\)の式によって計算できます。決まった数が何を意味するのか理解しましょう。
比例のグラフの書き方:0を通る直線
次に比例のグラフを描けるようにしましょう。比例の問題ではひんぱんにグラフが出題されます。グラフの書き方は以下のステップによって行いましょう。
- \(x\)と\(y\)の関係を示す表を作る
- グラフ上に点を取る
- 0を通る直線で結ぶ
例えば、\(y=2×x\)の比例のグラフはどのように描けばいいでしょうか。まず、以下のように\(x\)と\(y\)の関係を示す表を作りましょう。

次に、グラフに点を打ちます。例えば\(x\)が1のとき、\(y\)は2です。\(x\)が2のとき、\(y\)は4です。以下のようにグラフに点を記すのです。
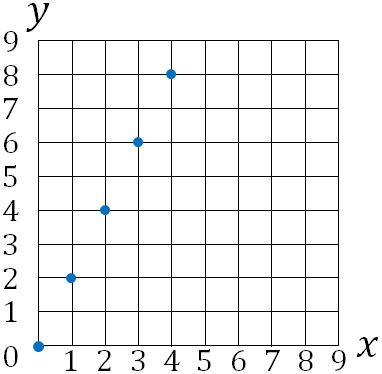
横軸は\(x\)を表し、たて軸は\(y\)を表します。最後に、0を通る直線で点を結びましょう。以下のようになります。
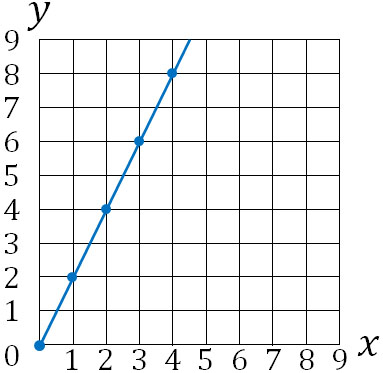
これによって、比例のグラフを描くことができます。
・0を通らない直線は比例ではない
なお比例のグラフを描くとき、必ず0を通ります。0を通らない場合、それは比例のグラフではありません。例えば、以下のグラフは比例ではありません。
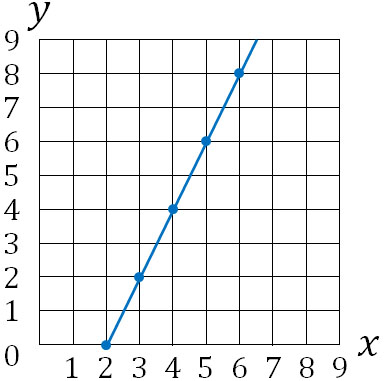
なぜ、比例のグラフは必ず0を通るのでしょうか。先ほど解説した通り、比例の式では以下のようになります。
- \(y=2x\)
- \(y=5x\)
- \(y=20x\)
そこで、\(x\)に0を入れてみましょう。そうすると、必ず\(y\)は0になります。すべての比例の式では、グラフは0を通るのです。
参考までに、直線のグラフで0を通らない場合、一次関数と呼ばれます。比例の式の親せきが一次関数です。一次関数は中学数学で学びます。
反比例とは何か:\(x\)が増えると\(y\)の値が減る
比例を学んだあと、反比例について学びましょう。比例では、\(x\)の値が増えると同じ割合で\(y\)の値が増えます。一方で反比例では、\(x\)の値が増えると同じ割合で\(y\)の値が減ります。
例えばたて\(x\)cm、横\(y\)cmの長方形の面積が30cm2のとき、以下の式を作ることができます。
- \(y=\displaystyle\frac{30}{x}\)
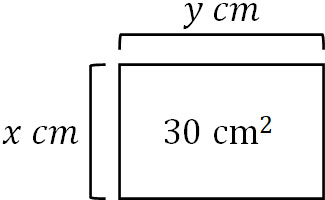
横とたての長さをかけると面積を出すことができます。そのため、\(x×y=30\)です。この式を変形すると、\(y=\displaystyle\frac{30}{x}\)になります。
イコール(\(=\))がある場合、同じ数を利用して両辺をかけたり割ったりすることができます。\(x×y=30\)について、両辺を\(x\)で割ると\(y=\displaystyle\frac{30}{x}\)になります。この式について、\(x\)と\(y\)を表にすると以下のようになります。

このように\(x\)が2倍になると、\(y\)は\(\displaystyle\frac{1}{2}\)倍になります。また\(x\)が3倍になると、\(y\)は\(\displaystyle\frac{1}{3}\)倍になります。このように\(x\)が増えることによって、同じ割合で\(y\)が減る場合は反比例です。
\(x\)と\(y\)で反比例の式を作る
比例と同じように、反比例の式を作れるようにしましょう。反比例の式では、例えば以下のようになります。
- \(y=\displaystyle\frac{15}{x}\)
- \(y=\displaystyle\frac{100}{x}\)
- \(y=\displaystyle\frac{27}{x}\)
なお、分数はわり算に変えることができます。そのため、以下の式についても反比例の式です。
- \(y=15÷x\)
- \(y=100÷x\)
- \(y=27÷x\)
いずれにしても、反比例ではこうした式を作るようにしましょう。以下が反比例の式になります。
- \(y=\displaystyle\frac{決まった数}{x}\)
- \(y=\)決まった数\(÷x\)
それでは、以下の問題では\(x\)と\(y\)についてどのような式を作ればいいでしょうか。
- 12Lが入る水そうがあります。1分で\(x\)Lの水を入れるとき、\(y\)分で水そうはいっぱいになります。
問題文から式を作りましょう。1分で\(x\)Lの水が入るため、\(y\)分後の水の量は\(x×y\)です。また水そうがいっぱいになるためには、合計で12Lの水が入ればいいとわかります。そのため、以下の式を作ることができます。
- \(x×y=12\)
この式を変形すると、\(y=\displaystyle\frac{12}{x}\)になります。こうして、反比例の式を作ることができます。
・反比例での決まった数の求め方
なお比例のときと同じように、反比例の式で決まった数を求められるようにしましょう。例えば反比例の場合、以下の表について決まった数(定数)は何でしょうか。

比例や反比例では、決まった数は同じです。また決まった数がわからない場合、決まった数を\(☐\)にしましょう。そうすると、反比例では\(x\)と\(y\)の関係は以下のようになります。
- \(y=\displaystyle\frac{☐}{x}\)
そこで、\(x\)と\(y\)の値を入れることで決まった数を求めましょう。例えば\(x\)が1のとき、\(y\)は90です。そのため、以下のようになります。
- \(90=\displaystyle\frac{☐}{1}\)
こうして、\(☐=90\)とわかります。なお、反比例の式では必ず決まった数は明確な一つの数字になります。そのため、ほかの\(x\)と\(y\)を利用しても決まった数(定数)をだすことができます。
- \(x\)が2のとき、\(y\)は45:\(45=\displaystyle\frac{☐}{2}\)
- \(x\)が3のとき、\(y\)は30:\(30=\displaystyle\frac{☐}{3}\)
- \(x\)が4のとき、\(y\)は22.5:\(22.5=\displaystyle\frac{☐}{4}\)
- \(x\)が5のとき、\(y\)は18:\(18=\displaystyle\frac{☐}{5}\)
- \(x\)が6のとき、\(y\)は15:\(15=\displaystyle\frac{☐}{6}\)
どの数字を利用しても、\(☐=90\)になります。一般的には、計算が簡単なので\(x\)が1のときの値を利用します。ただ、ほかの値を利用することによっても決まった数を得ることができます。
なお当然ですが、比例と同じように、反比例についても問題文が違えば決まった数(定数)は異なります。
反比例のグラフの書き方
次に反比例のグラフを描けるようになりましょう。反比例のグラフについては、以下のステップによってグラフを描きます。
- \(x\)と\(y\)の関係を示す表を作る
- グラフ上に点を取る
- 点をなめらかな曲線で結ぶ
まず、\(x\)と\(y\)の関係を示す表を作りましょう。例えば\(y=\displaystyle\frac{6}{x}\)のグラフはどのように描けばいいでしょうか。\(y\)の値が小数点になる場合を省くと、以下のような表になります。

次に、グラフに点を取りましょう。横軸は\(x\)を表し、たて軸は\(y\)を表すため、以下のように点を記入します。
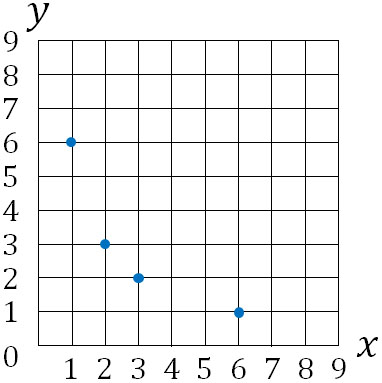
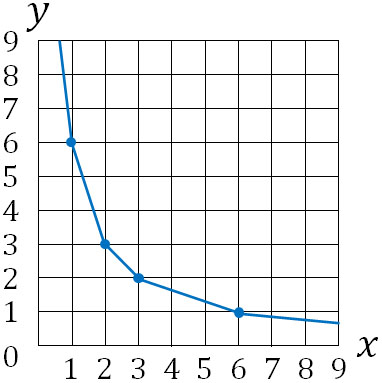
最後に、なめらかな曲線を利用して点をつなぎます。以下のようになります。
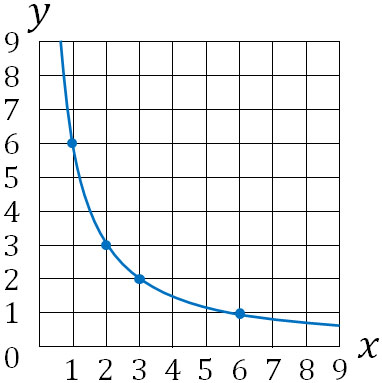
こうして、反比例のグラフを描くことができます。比例のグラフとは異なり、反比例のグラフでは0を通ることはありません。
・直線で点を結んではいけない
なお反比例のグラフを描くとき、直線を利用して点を結ばないようにしましょう。つまり、手がきによってなめらかな曲線を描く必要があります。そのため、以下のグラフは間違いです。
なぜ直線ではなく、反比例では曲線になるかというと、\(x\)の値が増えるとき、対応する\(y\)の値を記入していくと、曲線のグラフになるからです。グラフにはそれぞれ特徴があり、反比例のグラフの場合は曲線になるというわけです。
・\(x\)軸や\(y\)軸に線をくっつけてはいけない
ちなみに反比例のグラフを描くとき、ほかにも間違いやすいポイントがあります。それは、\(x\)軸や\(y\)軸に線をくっつけてはいけないことです。例えば、以下のグラフは線が\(x\)軸にくっついているので間違いです。

なぜ、反比例のグラフでは\(x\)軸や\(y\)軸とくっつく線を引くと間違いになるのでしょうか。反比例の場合、すでに解説した通り以下のような式になります。
- \(y=\displaystyle\frac{15}{x}\)
たとえ\(x\)の値が1000や10000と大きくなったとしても、\(y\)が0になることはありません。また\(y\)が1000や10000と大きくなったとしても、\(x\)が0になることはありません。つまり、反比例のグラフで\(x\)または\(y\)が0になることはありません。
このような理由によって、グラフの線が\(x\)軸や\(y\)軸とくっついていると間違いになります。
小学算数での比例・反比例の式とグラフ
\(x\)や\(y\)を利用する式を学ぶことによって、比例と反比例を理解できるようになります。比例や反比例にはわからない数が2つあるため、\(x\)と\(y\)を使うことで式を作るのです。
このとき、作れる式には2パターンあります。一つが比例であり、\(x\)が増加するのと同じ割合で\(y\)が増加します。また反比例の場合、\(x\)が増加するのと同じ割合で\(y\)が減ります。比例と反比例では式が異なるため、式の形を覚えるようにしましょう。
また比例と反比例を学ぶとき、グラフを描くことになります。そこでグラフの描き方を理解しましょう。比例は直線のグラフであり、反比例では手書きによるなめらかな曲線のグラフとなります。
比例と反比例にはルールがあります。そこでルールを理解し、式や表、グラフを作れるようにしましょう。