分数のたし算と引き算：分母が同じ場合と違う場合

分数の計算ではたし算と引き算をします。分数の計算で難しいのがたし算と引き算です。かけ算よりも、分数の計算ではたし算とひき算のほうが難しいです。

分数のたし算や引き算をする場合、一般的な方法とはやり方がちがいます。また、分母が同じなのかどうかによって計算方法が変わります。分母が違う場合、通分によって分母を同じ数にしなければいけません。

どのようにすれば、分数のたし算と引き算をすることができるのでしょうか。

分数のたし算と引き算では、必ず分母を同じにしなければいけません。そこで、分数のたし算と引き算の方法を解説していきます。

分母が同じ場合のたし算

分数のたし算をするとき、分子と分母の数を両方とも足してはいけません。たとえば、以下の計算は間違いです。

• \(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{5}\)

なぜ、この計算は間違いなのでしょうか。\(\displaystyle\frac{1}{2}\)は1を半分にした数であり、\(\displaystyle\frac{1}{3}\)は1を3等分した数です。

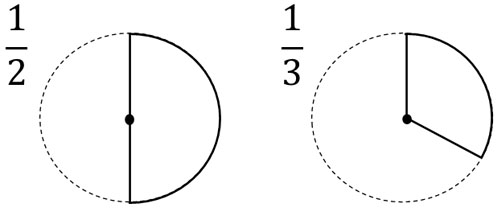
一方、\(\displaystyle\frac{2}{5}\)は1を5等分したあと、2つ集めた数です。そのため、\(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{5}\)とすると、ほんらいよりも数が小さいとわかります。

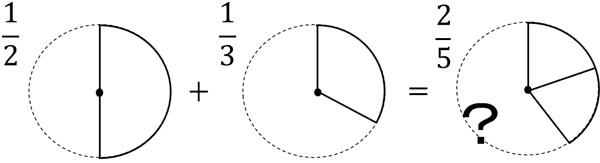
図をみると、この計算があきらかに間違いであると分かります。

なぜ、このような間違いが起きたのでしょうか。それは、分母を足したからです。分母というは、前述の通り「1を何等分するのか」を意味します。そのため、分母を足してはいけません。分母が同じとき、分母を変えないようにしましょう。

分母が同じ分数では、分母を変えず、分子のみたし算をします。たとえば、\(\displaystyle\frac{3}{4}\)には\(\displaystyle\frac{1}{4}\)が3つあります。また、\(\displaystyle\frac{2}{4}\)には\(\displaystyle\frac{1}{4}\)が2つあります。そのため、以下のようになります。

• \(\displaystyle\frac{3}{4}+\displaystyle\frac{2}{4}=\displaystyle\frac{5}{4}\)

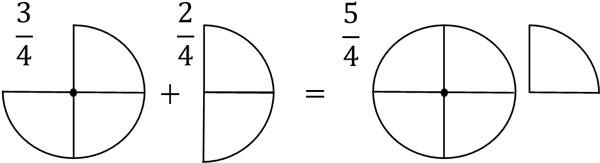
このように、分母は変わっていません。分数のたし算では、分子の数のみ変わります。分母というのは、「1を何等分しているのか」という性質を表しています。たし算では、数字の性質を変えてはいけません。そのため分母を変えず、分子のたし算のみをします。

分母が同じ場合の引き算

それに対して、分数の引き算はどのようにすればいいのでしょうか。先ほどと同じように、分母が同じ場合を考えてみましょう。

考え方はたし算と同じです。分母は分数の性質を表します。そのため、ひき算をするとき分母の数字は変わりません。その代わり、分子の数を引くようにしましょう。たとえば、以下のようになります。

• \(\displaystyle\frac{3}{4}-\displaystyle\frac{2}{4}=\displaystyle\frac{1}{4}\)

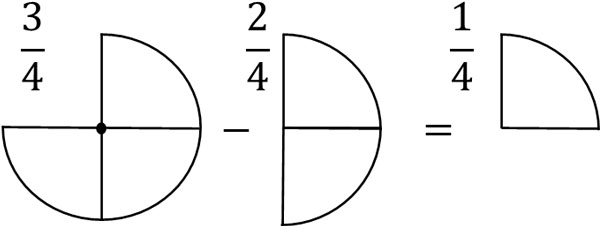
たし算ができるようになれば、分数の引き算を理解するのは難しくありません。同じ分母をもつ分数の引き算では、分母を変えず、分子の引き算のみをしましょう。

分母が違う場合、たし算や引き算ができない

一方で分母が違う場合、どのように足し算や引き算をすればいいのでしょうか。前述の通り、分母は分数の性質をあらわします。また性質が異なる数字の場合、足し算や引き算をすることができません。たとえば、以下の計算はどのようにすればいいでしょうか。

• \(\displaystyle\frac{3}{4}+\displaystyle\frac{1}{3}\)

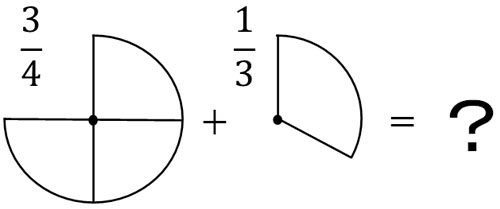
この状態のままでは、たし算をすることができません。分母が違うため、明確な答えをだすことができないのです。

そこで、分母をそろえるようにしましょう。分母が違う場合、数の性質が違うので足し算や引き算をすることができません。一方、分母が同じの場合、たし算や引き算をすることができます。分数でたし算や引き算をするとき、必ず分母を同じにしなければいけません。

分数の分母を同じにすることを通分といいます。そこで、通分をしましょう。

通分によって分母をそろえ、たし算や引き算をする

分数で通分をする場合、公倍数を利用しましょう。2つの分数について、分母を確認するのです。例えば、以下の分数はどのように計算すればいいでしょうか。

• \(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}\)

この計算をするため、通分をしましょう。分母を確認すると、数字は2と3です。2と3の最小公倍数は6です。そこで通分を行い、分母を以下のようにそれぞれ6にします。

• \(\displaystyle\frac{1}{2}=\displaystyle\frac{1×3}{2×3}=\displaystyle\frac{3}{6}\)
• \(\displaystyle\frac{1}{3}=\displaystyle\frac{1×2}{3×2}=\displaystyle\frac{2}{6}\)

こうして\(\displaystyle\frac{1}{2}\)を\(\displaystyle\frac{3}{6}\)に、\(\displaystyle\frac{1}{3}\)を\(\displaystyle\frac{2}{6}\)に変えることができました。分母が同じなので、たし算をすることができます。そこで、以下のように分数のたし算をしましょう。

• \(\displaystyle\frac{3}{6}+\displaystyle\frac{2}{6}=\displaystyle\frac{5}{6}\)

なお、ひき算についても同じ方法によって行います。例えば以下の計算では、先ほどと同じように通分をしましょう。

• \(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}\)

先に説明した通り、\(\displaystyle\frac{1}{2}\)は\(\displaystyle\frac{3}{6}\)です。また、\(\displaystyle\frac{1}{3}\)は\(\displaystyle\frac{2}{6}\)です。そのため、以下の式に変えることができます。

• \(\displaystyle\frac{3}{6}-\displaystyle\frac{2}{6}=\displaystyle\frac{1}{6}\)

たし算でも引き算でも、分母をそろえなければ計算をすることができません。そのため分母が違う場合、必ず通分をしましょう。

帯分数を使う足し算と引き算：くり上がりとくり下がり

ここまで、真分数と仮分数を利用して説明しました。帯分数でも、計算方法は同じです。分母が同じ場合、たし算や引き算をすることができます。例えば、以下はどのように計算すればいいでしょうか。

• \(1\displaystyle\frac{3}{4}+2\displaystyle\frac{2}{4}\)

\(1\displaystyle\frac{3}{4}\)は\(1+\displaystyle\frac{3}{4}\)を意味しています。また\(2\displaystyle\frac{2}{4}\)は\(2+\displaystyle\frac{2}{4}\)のことです。そこで、整数と分数を分けてたし算をしましょう。以下のようになります。

• \(1\displaystyle\frac{3}{4}+2\displaystyle\frac{2}{4}=3\displaystyle\frac{5}{4}\)

こうして、帯分数の計算をすることができました。なお、\(3\displaystyle\frac{5}{4}\)は分母よりも分子の数字が大きいです。そこで、分子の数を小さくしましょう。\(3\displaystyle\frac{5}{4}\)は以下のようになります。

• \(3\displaystyle\frac{5}{4}=3+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}\)

重要なのは、\(\displaystyle\frac{4}{4}=1\)であることです。そのため、\(3\displaystyle\frac{5}{4}\)を\(4\displaystyle\frac{1}{4}\)に変えることができます。くわしく確認すると、以下のようになります。

\(3\displaystyle\frac{5}{4}\)

\(=3+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}\)

\(=3+1+\displaystyle\frac{1}{4}\)

\(=4\displaystyle\frac{1}{4}\)

このように、帯分数ではくり上がりの計算をすることがあります。

・帯分数の引き算

一方で帯分数の引き算はどのようにすればいいのでしょうか。例として、\(3\displaystyle\frac{3}{4}-1\displaystyle\frac{2}{4}\)の計算をしてみましょう。帯分数には整数が含まれているため、整数と分数を分けて計算しましょう。以下のようになります。

• \(3\displaystyle\frac{3}{4}-1\displaystyle\frac{2}{4}=2\displaystyle\frac{1}{4}\)

整数を計算すると、\(3-1=2\)になります。そのため、帯分数の整数部分は2です。また、\(\displaystyle\frac{3}{4}-\displaystyle\frac{2}{4}=\displaystyle\frac{1}{4}\)になります。そのため、この帯分数の分数部分は\(\displaystyle\frac{1}{4}\)です。

一方、以下の計算はどのようにすればいいのでしょうか。

• \(3\displaystyle\frac{1}{4}-1\displaystyle\frac{2}{4}\)

分数の引き算をするとき、\(\displaystyle\frac{1}{4}-\displaystyle\frac{2}{4}\)を計算することはできません。そこで、整数から数を借りましょう。帯分数では、くり下がりの計算をすることがあるのです。つまり、\(3\displaystyle\frac{1}{4}\)を以下のように変えます。

\(3\displaystyle\frac{1}{4}\)

\(=2+1+\displaystyle\frac{1}{4}\)

\(=2+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}\)

\(=2\displaystyle\frac{5}{4}\)

この場合であれば、分数の引き算をすることができます。以下のようになります。

• \(3\displaystyle\frac{1}{4}-1\displaystyle\frac{2}{4}=2\displaystyle\frac{5}{4}-1\displaystyle\frac{2}{4}=1\displaystyle\frac{3}{4}\)

引き算をすることができない場合、くり下がりの計算をしましょう。

分母が異なる場合の帯分数の計算

なお、分母が異なるときの帯分数の計算方法はこれまで説明してきた方法と同じです。分母を同じにした後、たし算や引き算をしましょう。また、必要であればくり上がりまたはくり下がりの計算をしましょう。

例として、以下の計算をしてみましょう。

• \(3\displaystyle\frac{3}{4}+1\displaystyle\frac{2}{3}\)

分母は3と4です。3と4の最小公倍数は12です。そこで、分母を12にしましょう。以下のようになります。

• \(3\displaystyle\frac{3}{4}=3\displaystyle\frac{9}{12}\)
• \(1\displaystyle\frac{2}{3}=1\displaystyle\frac{8}{12}\)

通分をするとき、整数に変化はありません。変化するのは分数の分子と分母です。計算すると、答えは以下のようになります。

• \(3\displaystyle\frac{3}{4}+1\displaystyle\frac{2}{3}=3\displaystyle\frac{9}{12}+1\displaystyle\frac{8}{12}=4\displaystyle\frac{17}{12}\)

なお、\(4\displaystyle\frac{17}{12}\)の分子は分母よりも数字が大きいです。そこで、帯分数でのくり上がりをしましょう。計算は以下になります。

• \(4\displaystyle\frac{17}{12}=4+\displaystyle\frac{12}{12}+\displaystyle\frac{5}{12}=5\displaystyle\frac{5}{12}\)

こうして、分母が異なる帯分数の計算ができました。引き算についても、これまで説明した方法と同じやり方で計算することができます。

答えは仮分数と帯分数のどちらがいいのか

なお、分数の答えを出すとき仮分数と帯分数のどちらがいいのでしょうか。この答えはめいかくであり、仮分数で計算するようにしましょう。また答えについても、指定されていないのであれば、帯分数ではなく仮分数で答えを記しましょう。

理由としては、帯分数を使うのは小学生のみだからです。中学数学や高校数学、大学数学など、高度な数学で帯分数を使うことはありません。高度な数学では、必ず仮分数を使います。

帯分数を知識として知るのは問題ないものの、じっさいに使うことはほとんどありません。

プログラミングや建築、宇宙など、多くの分野で数学が使われます。このとき仮分数を使うことは多いものの、帯分数を使うことはまったくありません。そのため、帯分数ではなく仮分数で計算するようにしましょう。

分数のたし算と引き算の方法を理解する

慣れるまで分数の計算は難しいです。とくにたし算と引き算はやり方を覚えなければいけません。たし算と引き算をするためには、分母が同じである必要があります。

またたし算や引き算をするとき、分母は変わりません。分子のみ、たし算または引き算をするようにしましょう。そのためたし算や引き算をするとき、分母が同じ場合は分子の数字のみ変わります。

一方で分母が違う場合、足し算や引き算をすることができません。そこで、分母をそろえましょう。分母の数字を確認し、公倍数をみつけて通分するのです。

分数のたし算と引き算をするとき、正しい方法があります。どのように分数のたし算や引き算をすればいいのか理解しましょう。