線対称と点対称：小学算数の合同な図形

算数では図形の問題を学びます。その中の分野に合同ごうどうがあります。2つの同じ図形がある場合、それらを「合同な図形」といいます。

合同のがいねんを理解すれば、線対称せんたいしょうと点対称てんたいしょうがわかります。私たちの身の回りには、線対称や点対称の図形が多いです。そこで、どのような図形が線対称であり、点対称になっているのか理解するようにしましょう。

合同の図形を学べば、辺の長さや角度の大きさがわかるようになります。そこで、線対称と点対称について解説していきます。

移動や裏返しにより、重ね合わさる図形は合同

合同とはなんでしょうか。合同とは、2つの図形が同じであることを指します。例えば、以下の2つの図形は合同です。

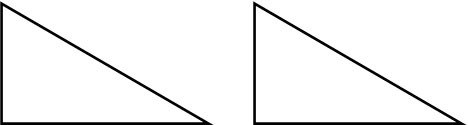
2つの図形をぴったりと重ねることができる場合、それらの図形は合同です。

また図形を移動したり、裏返したりするとき、重ねることのできる図形は合同です。例えば、以下の2つの図形は合同です。

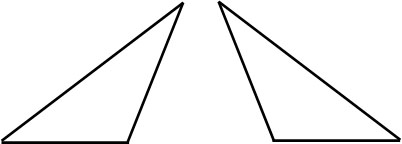
合同の図形を見つけるとき、裏返しをしてもいいことを理解しましょう。

なぜ、合同の図形を学ぶことが重要なのでしょうか。それは、合同の図形では対応する辺の長さや角度の大きさが同じだからです。2つの図形が合同な場合、重なり合う頂点を「対応する点」といいます。以下が対応する点です。

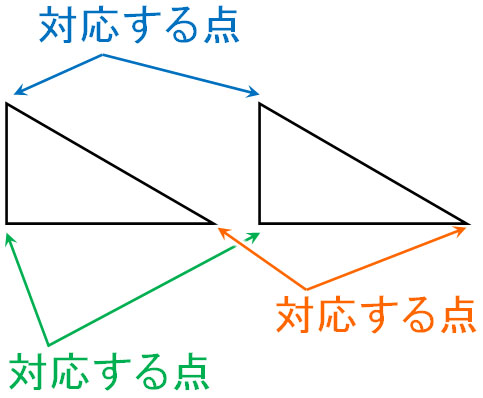
また合同な図形を確認するとき、同じ辺を「対応する辺」といいます。対応する辺では、辺の長さが同じです。また、同じ角度を「対応する角」といいます。対応する角では、角の大きさが同じです。

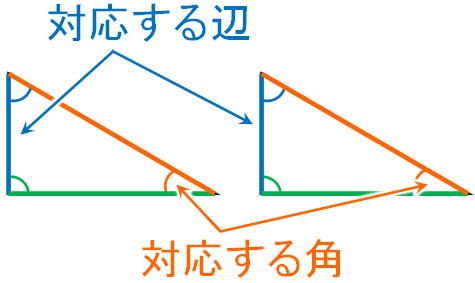
合同な図形では、対応する辺の長さと対応する角の大きさが等しいことを理解しましょう。

合同について理解すれば、線対称と点対称についても理解できるようになります。線対称や点対称とは何なのでしょうか。それぞれをかんたんに説明すると、以下のようになります。

図形がぴったり重なるというのは、図形が合同であることを意味しています。そこで、線対称と点対称についてくわしく確認していきましょう。

線対称というのは、折り曲げることによって重なる図形を指します。例えば、以下の図形は線対称です。

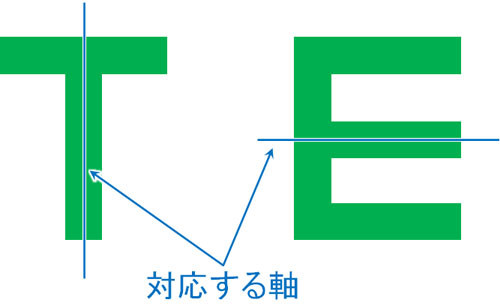
青色の線を利用して折り曲げると、両側の図形はぴったりと重なります。このような場合、線対称の図形になります。なお、図形を折り曲げるときの線を対応する軸といいます。

また、図形によっては対応する軸を複数もつことがあります。例えば、長方形には以下のように2本の対応する軸があります。

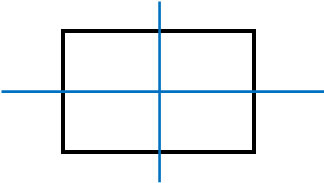
対応する軸は1本とはかぎらないことを理解しましょう。

一方、点対称とは何でしょうか。点対称とは、対称の中心を利用して180°回転させたとき、ぴったりと重なる図形を指します。

例えば、以下の図それぞれは点対称です。

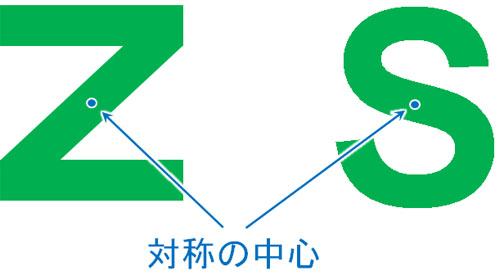
点対称の図形では、中心となる点があります。この点を対称の中心といいます。

それでは、どのようにして点対称の図形かどうかを判断すればいいのでしょうか。よりかんたんに理解する方法として、図を上下逆さまにしてみましょう。この場合、図形を回転させると以下のようになります。

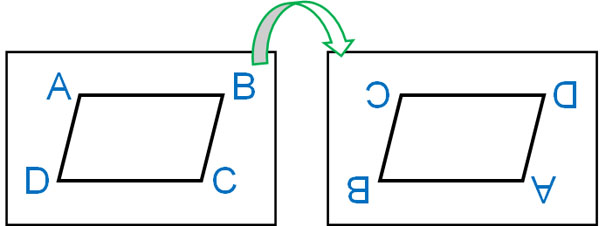
このように上下逆さまにしたとき、一致する図形は点対称の図形です。対称の中心を利用して180°回転させるというのは、図を上下逆さまにするのと意味が同じです。

なお点対称の場合、対応する点、対応する辺、対応する角度はそれぞれ以下のようになります。

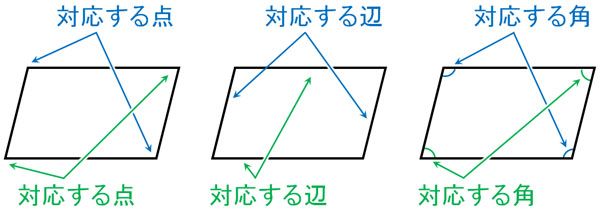
点対称の図形では、対応する辺や角度は必ず反対側にあります。

それでは、なぜ線対称や点対称を理解するのが重要なのでしょうか。この理由として、線対称や点対称の図形では以下の性質があるからです。

線対称や点対称の図形では、図形は合同です。線対称でも点対称でも、図形はぴったりと重なります。そのため、辺の長さと角の大きさが同じになります。つまり合同の図形を見つければ、辺の長さを知ることができます。

例えば、以下の図形で\(a\)と\(b\)の値は何でしょうか。

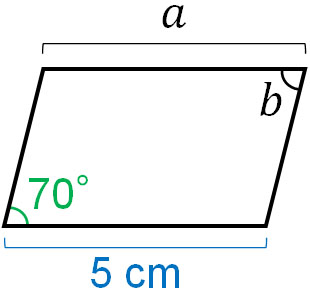
平行四辺形は点対称の図形です。対応する辺の長さは等しいため、\(a\)の長さは5cmです。また対応する角は等しいため、\(b\)は70°です。こうして、辺の長さや角度を求めることができます。

形が同じ図形は合同です。合同な図形を探せば、辺の長さや角度を知ることができます。対応する辺の長さは等しく、対応する角の大きさは等しいからです。

また合同のがいねんを理解したあと、線対称と点対称について学ぶことになります。図形を折り曲げるとき、重なる場合は線対称の図形です。また対称の中心を利用して180°回転させ、重なる場合は点対称です。

これらの図形では、対応する辺と対応する角が等しいという性質があります。この性質を利用して辺の長さや角度を見つけるようにしましょう。