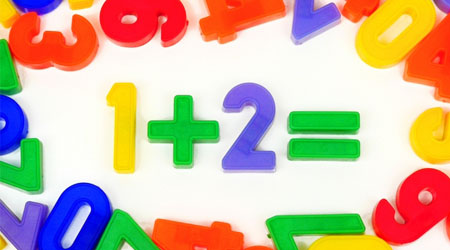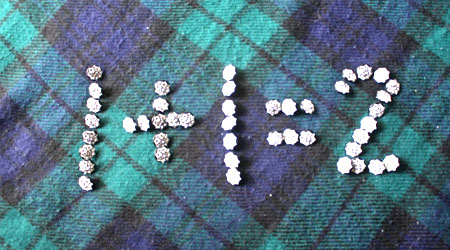小学算数で学ぶことの一つが約数と倍数です。わたしたちの日常生活でも約数と倍数は頻繁に利用されます。そのため、どのような内容なのか理解しましょう。
約数と倍数では、両方ともかけ算やわり算を利用して問題を解きます。考え方は違いますが、似た方法によって問題を解いていくことになります。
またこのとき、約数では最大公約数という言葉があります。倍数については、最小公倍数という言葉があります。2つ以上の数字を比べることによって、最大公約数と最小公倍数を出せるようになります。日常生活で約数や倍数が役立つのは、最大公約数や最小公倍数を学ぶからです。
そこで、どのように約数と倍数の問題を解けばいいのか解説していきます。
もくじ
約数とは何か?わりきれる数が約数
まず、約数とは何なのでしょうか。整数でわり算をするとき、わりきれる数を約数といいます。
たとえば、12の約数はどのようになるのでしょうか。12に対して、わりきれる整数が約数です。そこで、\(☐\)に当てはまる数字は何か考えてみましょう。
- \(12÷☐\)
12の約数を見つけるためには、12のわり算をしましょう。以下の整数であれば、あまりの数なしにわり算をすることができます。

つまり12の約数は「1、2、3、4、6、12」です。約数では、わりきれる整数を見つけるようにしましょう。
かけ算で約数を見つけていく
先ほど解説した方法はもっとも一般的な方法です。ただこの約数の求め方では、答えを見逃してしまうことがよくあります。たとえば12の約数を答えるとき、「1、2、3、4、12」としてしまうのです。この場合、6が抜けているので不正解です。
そこで、できるだけミスを少なくしなければいけません。そこで約数では、わり算ではなく、かけ算によって答えを見つけるようにしましょう。そこで、以下のようにかけ算をすることで答えが12になる整数を見つけましょう。
- \(1×12=12\)
- \(2×6=12\)
- \(3×4=12\)
このようにすれば、答えを出すことができます。整数のかけ算によって12になるのであれば、「わり算によってあまりの数なしにわりきれる」のと同じことを意味します。そのため、かけ算で利用したすべての整数が約数になります。
なお、\(2×6=12\)と\(6×2=12\)は意味が同じです。そのため\(2×6=12\)を思いつけば、2と6が約数になると分かります。わり算のように、わりきれる整数を一つずつすべて見つける必要はありません。約数を探すとき、かけ算を使うほうが効率的です。
公約数と最大公約数の考え方
約数とは何かを理解すれば、公約数と最大公約数を学ぶことができます。さきほど、一つの数字について約数を求めました。一方で2つ以上の数に共通する約数を公約数といいます。
たとえば、24と30の公約数は何でしょうか。答えを出すためには、24と30の約数をすべて書き出してみましょう。以下のようになります。
- 24の約数:1、2、3、4、6、8、12、24
- 30の約数:1、2、3、5、6、10、15、30
この中で共通する数字は何でしょうか。共通する約数は以下のようになります。
- 24と30の公約数:1、2、3、6
このようにして、24と30の公約数を見つけることができました。
なお公約数の中でも、最も大きい数字を最大公約数といいます。先ほどの公約数の中で、最も大きい数は6です。そのため、24と30の最大公約数は6といえます。
公約数や最大公約数を見つけるためには、2つ以上の数字についてそれぞれ約数を出していく必要があります。そのため、共通する約数を確認しましょう。
倍数とは何か?整数倍した数が倍数
一方、約数と同時に学ぶのが倍数です。倍数とは何なのでしょうか。特定の数について、自然数を利用してかけ算したものを倍数といいます。
たとえば、12の倍数は何でしょうか。12の倍数を見つけるためには、12に対して順に自然数のかけ算をしましょう。以下のようになります。
- \(12×1=12\)
- \(12×2=24\)
- \(12×3=36\)
- \(12×4=48\)
- ……
このように「12、24、36、48…」が12の倍数です。自然数は無限に存在するため、倍数は無限にあります。そのため、12の倍数もたくさんあります。いずれにしても、特定の数字に対して自然数をかけ、出てきた答えが倍数です。
特定の数でわりきれるのが倍数:あまりの数を確認する
かけ算をすることによって倍数を出すことができます。ただ倍数を見つけるとき、わり算をすることがよくあります。なぜ、かけ算ではなくわり算を利用するのでしょうか。
倍数というのは、特定の整数でわりきることができる数といえます。先ほど解説した約数と考え方が似ており、わりきれる数があるからこそ倍数といえます。
たとえば、以下の数字のうち14の倍数はどれでしょうか。
- 48、70、100、108、112
この答えを出すためには、わり算をしましょう。そうすると、わりきれる場合とあまりの数が出る場合の2パターンに分かれます。以下のようになります。
- \(48÷14=3\) あまり 6
- \(70÷14=5\)
- \(100÷14=7\) あまり 2
- \(108÷14=7\) あまり 10
- \(112÷14=8\)
答えが5または8の場合、わりきることができると分かりました。そのため、先ほどの数字の中で14の倍数は70と112と分かります。
事実、\(5×14=70\)であり、また\(8×14=112\)です。わり算はかけ算でもあります。約数と同じように、倍数の答えを求めるときはかけ算とわり算の両方を利用しましょう。
公倍数と最小公倍数の求め方
ここまでの内容を理解すれば、公倍数と最小公倍数について理解できるようになります。2つ以上の数字を比べるとき、共通する倍数を公倍数といいます。
たとえば、6と8の公倍数は何でしょうか。この答えを出すためには、6と8の倍数をそれぞれ書き出してみましょう。以下のようになります。
- 6の倍数:6、12、18、24、30、36、42、48…
- 8の倍数:8、16、24、32、40、48、56、64…
このように倍数を書きだしていくと、24と48が共通しています。そのため、6と8の公倍数は24と48になります。
実際には、6の倍数と8の倍数は無限に続いていきます。そのため、6と8の公倍数は「24、48、72、96、120……」と続いていきます。そのためすべての公倍数を出すのは不可能ですが、このように一部の公倍数を見つけることができればいいです。
こうした公倍数のうち、最も小さい数字を最小公倍数といいます。6と8の公倍数であれば、最小公倍数は24といえます。
最小公約数と最大公倍数という言葉はない
最大公約数と最小公倍数という言葉について学びました。一方で、最小公約数と最大公倍数という言葉はありません。
公約数の中で、最も小さい数は何でしょうか。それは1です。すべての整数では、最も小さい約数は1になります。最小公約数は必ず1になるため、計算する意味がありません。そのため最小公約数ではなく、最大公約数について問題が出されます。
また、最大公倍数という言葉もありません。前に説明した通り、倍数は無限に存在します。おさらいすると、6と8の公倍数は「24、48、72、96、120……」と永遠と続きます。
数がどれだけ大きくなったとしても、最大の公倍数を見つけることはできません。これが、最大公倍数が存在しない理由です。最大公倍数ではなく、最小公倍数でなければ数字を見つけることはできません。
日常生活で利用される約数と倍数
それでは、こうした知識がどのように日常生活で役に立つのでしょうか。約数や倍数はあらゆる場面で応用されています。その中でも、より身近な買い物で考えてみましょう。
たとえば、以下のジュースはどちらのほうがお得でしょうか。
- 5本のジュースで800円
- 8本のジュースで1200円
この問題を考えるためには、最小公倍数を計算しましょう。5と8の最小公倍数は何でしょうか。以下のように、5と8の公倍数を書き出してみましょう。
- 5の倍数:5、10、15、20、25、30、35、40…
- 8の倍数:8、16、24、32、40、48、56、64…
このように、最小公倍数は40と分かりました。つまり、ジュース40本を買うときの値段を比較すれば、どちらが安いのか分かります。そこで、以下のように計算しましょう。
- 800円(5本) × 8セット = 6400円
- 1200円(8本) × 5セット = 6000円
同じ40本のジュースを購入するにしても、「8本のジュースで1200円」を買うほうが安いと分かります。かんたんな例を利用しましたが、このように日常生活のさまざまな場面で約数と倍数が応用されています。
算数で重要な約数と倍数を理解する
小学算数で学ぶ内容の一つが約数と倍数です。整数のかけ算とわり算をすることができれば、約数と倍数の考え方を理解することができます。
特定の数について、わりきることのできる整数が約数です。約数を出すとき、わり算ではなくかけ算を使うと計算ミスが減ります。また2つ以上の数字を比べたとき、共通する約数が公約数です。また最も大きい公約数を最大公約数といいます。
一方、整数倍した数が倍数です。倍数は無限に続いています。また2つ以上の数を比べたとき、共通する倍数を公倍数といいます。公倍数の中でも、最も小さい数を最小公倍数といいます。
これら約数と倍数の考え方を理解しましょう。最大公約数や最小公倍数は私たちの日常生活でも応用されており、これらを利用した計算が日々の暮らしに役立つようになります。