日常生活でグラフが利用される場面は多いです。たとえばニュースでは、グラフが何度も利用されます。数字だけが並んでいる状態では、データが何を表しているのか理解しにくいです。一方でグラフに直せば、どういう状態なのか簡単に理解できるようになります。
こうしたグラフの中でも、割合を利用するグラフに帯グラフと円グラフがあります。全体の数を100%とするとき、それぞれの要素が何パーセントなのかをグラフで表すのです。
割合や百分率(パーセント)を理解したあと、帯グラフと円グラフを学びましょう。そうすれば、データが何を意味しているのかわかるようになります。
そこで割合を表すグラフで重要な帯グラフと円グラフについて、見方や割合の計算方法を解説していきます。
もくじ
割合を表すグラフには帯グラフと円グラフがある
グラフにはさまざまな種類があります。その中でも、割合を表すグラフが存在します。それが帯グラフと円グラフです。帯グラフは棒状のグラフであり、円グラフでは円に要素を記していきます。
以下のグラフが帯グラフと円グラフです。
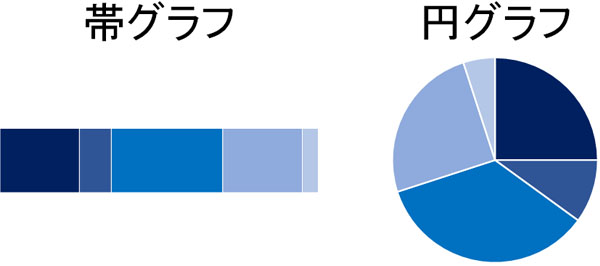
このようなグラフを利用することによって、データをわかりやすく示すのです。たとえば、以下のデータを見たときに内容を一瞬で判断できるでしょうか。
| 好きなスポーツ | 割合 |
| テニス | 25% |
| バスケットボール | 10% |
| サッカー | 35% |
| バレーボール | 25% |
| その他 | 5% |
一方、以下のように図になっているとどうでしょうか。
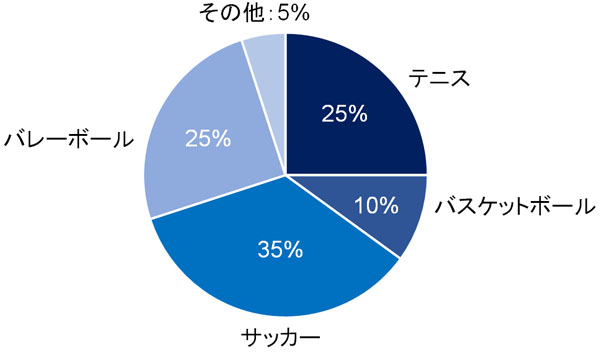
このように図に表すとわかりやすくなります。そのため、帯グラフや円グラフがひんぱんに利用されるのです。
すべて足すと必ず100%になる
帯グラフや円グラフは見てわかりやすいだけでなく、割合を表すグラフでもあります。より具体的にいうと、百分率(パーセント)を利用することによってグラフを作ります。そのため全体の量を100%とするとき、グラフのそれぞれの要素がどれだけの割合をもっているのかを示すのが帯グラフと円グラフです。
すべての要素を足すとき、80%や90%になることはありません。そのようなグラフだと理解しにくいため、グラフにする意味がありません。帯グラフや円グラフでは、すべてのケースで全体の合計が100%です。
そのため要素の個数がそれぞれいくらなのかを知るためには、全体の量を知る必要があります。たとえば先ほどのグラフでは、テニスが好きな人の割合は25%です。それでは、テニスが好きなのは何人でしょうか。
全体の数がわからない場合、答えを出すことができません。一方、全体の人数が100人であればどうでしょうか。100人のうち、25%の人で「テニスが好き」と回答しています。そのため、テニスが好きな人数は25人とわかります。
いずれにしても全体は必ず100%になるため、この性質を利用して計算しましょう。
グラフから割合を求める
それでは、実際に帯グラフや円グラフの問題を解いてみましょう。たとえば以下のような帯グラフがあるとき、カレーが好きな人の割合はいくらでしょうか。

先ほど解説した通り、帯グラフや円グラフでは全体の割合が必ず100%になります。全体の割合が90%だと、非常にわかりにくいグラフになるため意味がありません。そのため、全体の割合は100%でなければいけません。
そこでカレーが好きな人の割合を計算するため、ピザとハンバーガーが好きな人の割合をたしましょう。その後、100%からピザとハンバーガーが好きな人の割合をひきます。以下のような計算になります。
- \(100-(30+50)=20\)
こうして、カレー好きの人は全体の20%であるとわかります。グラフを確認することによって、割合をだすことができるのです。
割合を利用し、個数や人数を求める
次に、割合のグラフを利用することによって個数(または人数)を求めるようにしましょう。たとえば先ほどのグラフについて、全体の人数が70人の場合、カレー好きの人は何人でしょうか。
全体の人数が70人であり、そのうち20%がカレーが好きです。20%を小数にすると0.2です。そのため、以下の計算によって答えをだすことができます。
- \(70×0.2=14\)
全体の数がわかっている場合、百分率を利用することによって要素に含まれている個数や人数がわかります。
グラフの要素を使い、割合をだす
次に、グラフを構成している要素同士がどのような割合になっているのか計算できるようにしましょう。例として、先ほどと同じ以下のグラフを利用します。

この帯グラフについて、ピザが好きな人はハンバーガーが好きな人の何倍でしょうか。
ピザが好きな人は30%であり、ハンバーガーが好きな人の割合は50%です。また先ほどの問題文について、「ハンバーガーが好きな人(50%)を基準にして、\(☐\)倍したらピザが好きな人の割合(30%)になるのか」と言い換えることができます。つまり、以下の式を作れます。
- \(50×☐=30\)
この式を解くと、\(☐\)に入る数字は0.6です。そのためピザが好きな人は、ハンバーガーが好きな人の0.6倍であるとわかります。2つの割合を利用することによって、割合同士の関係を計算することができるのです。
割合のグラフの性質を学ぶ
割合や百分率(パーセント)を学ぶことによって、割合のグラフを理解できるようになります。割合のグラフには帯グラフや円グラフがあります。
割合のグラフを利用する場合、必ず全体で100%になります。全体の個数がいくらなのかに関係なく、いずれにしてもすべてを合計すると100%になるのです。これにより、それぞれの要素のパーセントがわかります。
また要素がもつパーセントがわかれば、全体の数を利用することによって、いくつの個数(または人数)がそれぞれの要素に含まれているのか計算できます。それぞれの要素ごとの関係について、割合をだすこともできます。
グラフが利用される場面はたくさんあります。そこで帯グラフと円グラフについて、グラフが何を意味しているのか理解するようにしましょう。