小学算数で学ぶ内容として文字と式があります。代数式と呼ばれており、\(x\)や\(y\)などの文字を利用することによって式を作ります。
ただ代数式はすでに全員が習っており、これまでに何度も式を作ったことがあります。算数では、わからない数を\(☐\)にして式を作ります。\(x\)や\(y\)などの文字を用いた式というのは、要は\(☐\)を含む式のことです。つまり\(☐\)を含む式を理解できる場合、全員が代数式がわかるようになります。
中学や高校、大学の数学では全員が文字を利用して式を作ります。小学算数で学ぶ文字を用いた式を理解できない場合、高度な数学の問題を解くことができません。
代数式を学び、式を作れるようになるのは重要です。そこでどのように文字を利用して計算式を作り、問題を解けばいいのか解説していきます。
もくじ
\(☐\)を使う式:足し算・引き算・かけ算・割り算
小学校では、算数ですべての人が\(☐\)を利用する計算問題を解いたことがあると思います。例えば、以下のような式です。
- \(3+☐=9\)
- \(☐-5=3\)
- \(7×☐=14\)
- \(6÷☐=2\)
このように、わからない数を\(☐\)にします。その後、\(☐\)に当てはまる数字を探します。足し算や引き算、かけ算、割り算を含め、すべての人で\(☐\)を含む式を計算したことがあると思います。代数式(文字式)を学ぶとき、\(☐\)を利用する計算式を思い出しましょう。
\(☐\)を利用し、問題文から式を作る
次に、\(☐\)を利用して問題文を作りましょう。文字を使った式では、わからない数を\(☐\)とします。その後、式を作ります。文字式を理解するため、まずは\(☐\)を利用する計算を考えましょう。
例えば、以下の問題の答えは何でしょうか。
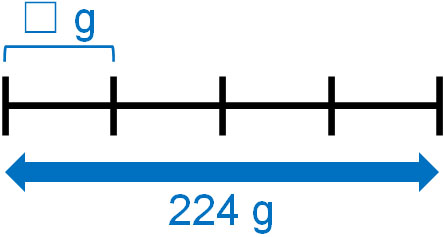
- 箱が4つのとき、全体の重さは224gでした。一つの箱の重さはいくらですか?
この問題文でわからない数は何でしょうか。問われているのは「一つの箱の重さ」であり、これがわかっていません。そこで、一つの箱の重さを\(☐\)とします。
一つ\(☐\)gの箱が4つあるとき、全体の重さは224gです。そのため、以下の式を作ることができます。
- \(☐×4=224\)
この式を解くと以下のようになります。
\(☐×4=224\)
\(☐=224÷4\)
\(☐=56\)
答えは56gです。こうして、\(☐\)を利用することによって一つの箱の重さを計算することができます。
わからない数字を\(☐\)ではなく\(x\)にする
ここまでの内容を理解できる場合、代数式を利用することができます。先ほど、わからない数を\(☐\)にしました。一方で文字式では、わからない数を\(☐\)ではなく\(x\)にします。つまり\(☐\)を\(x\)にしただけであり、ほかに違いはありません。
先ほど、\(☐\)を利用することで以下の式を作りました。
- \(☐×4=224\)
この式について、以下のように\(☐\)を\(x\)に変えると代数式(文字式)になります。
- \(x×4=224\)
それでは、実際に文字を利用して式を作ってみましょう。以下の問題の答えは何でしょうか。
- 図書館に20人いたが、2時間後には14人に減った。何人の人が帰りましたか?
何人の人が帰ったのかわからないため、帰った人数を\(x\)にします。20人から\(x\)人が減った結果、14人になりました。そのため、以下の式を作ることができます。
- \(20-x=14\)
この式を解くと、答えは\(x=6\)になります。こうして、答えは6人とわかります。このように理解すると、\(☐\)を利用する式と文字式は同じであるとわかります。
答えを\(y\)にして式を作る
それでは、なぜ私たちは\(☐\)ではなく文字を利用して式を作るのでしょうか。この理由として、わからない数が複数になることがひんぱんにあるからです。
わからない数が2つ以上ある場合、\(☐\)を利用すると式を作ることができません。そこで、\(x\)とは別に\(y\)を利用することによって式を作ります。
そのためわからない数が2つあるとき、\(x\)と\(y\)を利用しましょう。例えば、以下の関係を式にすると、どのようになるでしょうか。
- 横が12cm、たてが\(x\)cmの面積は\(y\)cm2です。
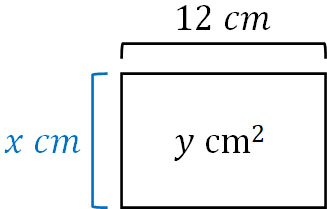
面積を出すためには、横とたてをかければいいです。わかっていない数字(\(x\)と\(y\))を利用すると、以下の式を作ることができます。
- \(12×x=y\)
こうして、\(x\)と\(y\)を使って式を作ることができます。それでは、以下であればどのような式を作ることができるでしょうか。
- 1000mLの水があります。あなたが\(x\)mLを飲むとき、残りの水の量は\(y\)mLです。
最初に1000mLの水があり、\(x\)mL飲むと、当然ながら\(x\)mLの水が減ります。そのため、以下の式を作ることができます。
- \(1000-x=y\)
いずれにしても、このようにわからない2つの数字があるとき、\(x\)と\(y\)を利用して式を作れるようにしましょう。
変数(\(x\))と答え(\(y\))の関係を式にする
なお\(x\)と\(y\)を利用して式を作るとき、算数(数学)にはルールがあります。以下のルールを覚えましょう。
- 変えることのできる数(変数):\(x\)
- 得たい答え:\(y\)
\(x\)には、どのような数であっても入れることができます。また\(x\)に数字を入れることによって、\(y\)の値(答え)が決まります。この説明では理解できないと思うので、先ほどの例題を確認しましょう。
- 横が12cm、たてが\(x\)cmの面積は\(y\)cm2です。
この関係を式にすると\(12×x=y\)です。
前述の通り、\(x\)にはあらゆる数字を入れることができます。\(x\)の値は3でもいいし、10000でもいいです。このように、\(x\)の値を自由に変えることができます。こうした数を変数といいます。\(x\)というのは、別名で変数と呼ばれるのです。
また\(x\)に数字を入れると、\(y\)の値が決まります。要は、答えを得ることができます。数学(算数)では、「\(x\)の値が決まることによって得られる答え」を\(y\)にするようにルールが決められています(高校以上の高度な数学では例外があります)。
先ほどの例であれば、\(x\)の値(たての長さ)が決まることによって\(y\)の値(面積)が決まります。このように、変えることのできる数(どのような数字を入れてもいい数)を\(x\)にして、得られる答えを\(y\)にしましょう。
\(x\)または\(y\)に数字を入れ、答えを得る
式を作れるようになったら、\(x\)に数字を入れることによって答え(\(y\))を得ましょう。例えば、以下の関係を式にしましょう。
- ミカンが入っている箱が3つ、また箱の外にミカンが6つあります。1つの箱に入っているミカンの数が\(x\)個のとき、ミカンの合計個数を求める式を作りましょう。
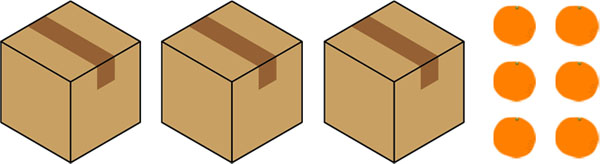
箱に入っているミカンの数はわかりません。つまり、一箱の中にあるミカンの数をあなたが自由に変えることができます。一つの箱に5個のミカンを入れてもいいし、1000個のミカンを入れてもいいです。
また一箱に入っているミカンの数が決まれば、ミカンの合計個数も決まります。そこで、ミカンの合計個数(答え)を\(y\)としましょう。また箱の外にミカンが6個あるため、ミカンの合計個数は以下の式によって得ることができます。
- \(3×x+6=y\)
一箱に5個のミカンが入っている場合、\(x\)の値は5なので、\(y\)の値は21です。また一箱に10個のミカンが入っている場合、\(x\)の値は10なので、\(y\)の値は36です。
または、\(y\)の値がわかっていることもあります。例えば先ほどの問題について、ミカンの合計個数が24個の場合、一つの箱の中にはいくつのミカンが入っているでしょうか。ミカンの合計個数が24であるため、\(y\)の値は24です。そのため、以下の式を作ることができます。
- \(3×x+6=24\)
そこで、この式を解きましょう。以下のようになります。
\(3×x+6=24\)
\(3×x=24-6\)
\(3×x=18\)
\(x=18÷3\)
\(x=6\)
こうして、「ミカンの合計個数が24の場合、一箱の中には6個のミカンがある」とわかります。
このように2つのわからない数字がある場合、一つの値(\(x\)または\(y\))を入れることによって、ほかの数字を得ることができます。
\(x\)の値によって\(y\)の値が決まる式を関数という
参考までに、文字を用いた式を学ぶときは関数という言葉を理解するようにしましょう。関数のがいねんは難しくないものの、多くの人が関数の意味を理解していないため、中学や高校の数学を嫌いになります。
関数というのは、数字を入れることによって答えを得られる式と理解しましょう。先ほど、ミカンの個数の関係を表す以下の式を作りました。
- \(y=3×x+6\)
もし\(x\)の値が2の場合、\(y\)の値は12です。また\(x\)の値が3の場合、\(y\)の値は15です。このように\(x\)の値が決まることによって\(y\)の値を決めることができます。
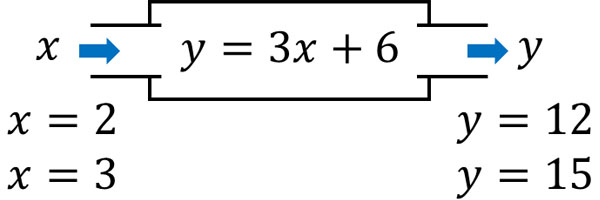
こうした関係の式を関数といいます。\(x\)(または\(y\))の値が決まると、もう一方の値が決まる式が関数です。文字を用いた式では、\(x\)と\(y\)を利用して式を作ります。文字を利用して式を作るというのは、関数を作っているのと意味が同じです。
代数式(文字式)を理解し、式を作れるようにする
\(x\)や\(y\)などの文字を利用して式を作るとなると、難しいように思えてしまいます。ただ小学算数を学んでいる人であれば、すべての人ですでに文字式を利用しています。これまでに\(☐\)を利用して式の計算をしたり、式を作ったりしたことがあると思います。
そこで代数式を利用する場合、\(☐\)の代わりに\(x\)を利用しましょう。わからない数を\(x\)にすれば、文字を利用した式を作れます。
また文字を用いた式では、得たい答えを\(y\)にしましょう。代数式ではわからない数が2つ出てくるため、答えを\(y\)にして、自由に変更できる数を\(x\)にします。また\(x\)と\(y\)を利用して式を作った後、\(x\)または\(y\)の値がわかれば、もう一方の値を計算することができます。この関係にある式を関数といいます。
文字式を学ぶとき、\(☐\)を利用する計算式をおさらいしましょう。そうすれば、\(x\)と\(y\)を利用して式を作れるようになります。