小学校の算数でたし算と引き算を学びます。たし算や引き算を勉強するとき、つまずきやすいポイントがくり上がりの計算です。どのように計算すればいいのかわからないのです。おなじく、引き算でも多くの小学生がくり下がりの計算でつまずきます。
整数のたし算や引き算をするとき、重要な数が10です。計算をするとき、10をみつけることによってくり上がりやくり下がりの計算ができるようになります。
そこで、どのように整数のたし算と引き算をすればいいのか解説していきます。
もくじ
たして10になる数をみつける
算数では、以下の数を整数といいます。
- 0、1、2、3、4、5、6、7、8、9……
これらの数をたすとき、くり上がりがないときは苦労なく計算することができます。以下のようになります。
- \(1+6=7\)
- \(3+4=7\)
- \(7+2=9\)
それでは、くり上がりのあるたし算ではどのように計算すればいいのでしょうか。たとえば、以下の計算です。
- \(3+8\)
- \(6+6\)
くり上がりのあるたし算を計算するためには、たして10になる数をみつけられるようになるようにしましょう。次の☐にはいる数字は何でしょうか。
- \(2+☐=10\)
- \(6+☐=10\)
- \(5+☐=10\)
- \(1+☐=10\)
- \(9+☐=10\)
- \(8+☐=10\)
- \(7+☐=10\)
- \(3+☐=10\)
- \(4+☐=10\)
答えは次のようになります。
- (1) 8、(2) 4、(3) 5、(4) 9、(5) 1、(6) 2、(7) 3、(8) 7、(9) 6
それぞれの答えをすべて覚えるようにしましょう。どの数字をくわえることによって、10の数字をつくれるのか理解していなければ、くり上がりのあるたし算を計算することができないからです。
くり上がりのあるたし算の計算
それでは、どのようにしてくり上がりのあるたし算を計算すればいいのでしょうか。たし算をするとき、くり上がりがある計算では数字を2つにわけて10の数字をつくりましょう。たとえば、以下の計算はどのようにすればいいのでしょうか。
- \(6+9\)
まず、左の数(6)にたいして、なにをたせば10になるのか考えましょう。6にたいして、4をたせば10になります。そこで、以下のように数字をわけましょう。
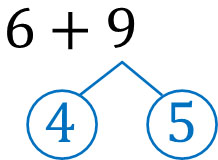
\(9=4+5\)です。つまり、9は4と5にわけることができます。そのあと、6と4をたして10にします。
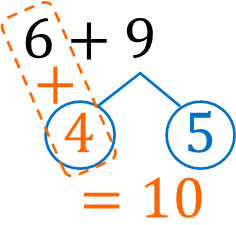
さいごに、残った5をたします。そうすると、答えとして15ができます。まとめると、以下のようにしてくり上がりのあるたし算を計算しましょう。
- 左の数になにをたせば、10になるのか考える
- 右の数をわける
- すべての数をたす
「なにをたせば10になるのか」を思いつくことができなければ、くり上がりのたし算を計算することはできません。そこで、たして10になる数字をすべて覚えるようにしましょう。
2ケタと1ケタのたし算
それでは、2ケタと1ケタのたし算はどのようにすればいいのでしょうか。さきほどと考え方はおなじであり、たして10になる数をさがしましょう。
たとえば、以下の計算をします。
- \(27+5\)
さきほどとは違い、10の数字を作ることはできません。そのかわり、数字をたして30の数字を作ることができます。つまり、10や20、30とキリのよい数を作るようにしましょう。
27にたいして、なにをたせば30になるでしょうか。27に3をくわえれば30になります。そこで、5を以下のようにわけましょう。
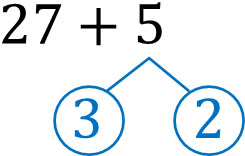
27に3をたせば30になります。また、残った2をたすことで答えは32です。さきほどと考え方はおなじです。いずれにしても、キリのよい数をみつけて計算しましょう。
くり下がりのある引き算の計算
たし算を学んだあと、引き算を理解しなければいけません。くり下がりのある引き算でも、さきほどのたし算と同じように考えて計算しましょう。つまり10や20、30などキリのよい数をみつける必要があります。
たとえば、以下の答えはなんでしょうか。
- \(54-9\)
54にたいして、どの数字を引けばキリのよい数になるでしょうか。54から4を引くと、50になります。そのため、以下のように9をわければいいとわかります。
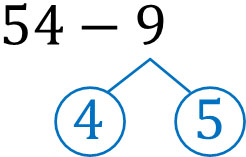
9は4と5にわけることができます。そのあと、以下のように計算しましょう。
- 54から4を引く:数字は50
- 次に50から5を引く:答えは45
この計算は以下と意味がおなじです。
- \(54-4-5\)
\(54-9\)の計算をするとき、数字をわけると計算しやすいです。たし算でも引き算でも、このやり方によって計算しましょう。
慣れてきたら、数字をわけなくても計算できるようになります。ただ慣れるまで、この方法によって算数の計算をするといいです。
算数で2ケタや3ケタのたし算の筆算をする
それにたいして、2ケタや3ケタのたし算の計算はどのようにすればいいのでしょうか。1ケタのたし算をするときに比べると、複雑な計算になります。
たとえば、以下の計算はどのようにすればいいのでしょうか。
- \(47+85\)
2ケタのたし算をするとき、以下の式をつくります。
\(\begin{array}{rr}
& 47\\
+\big{)}&85\\
\hline
\end{array}\)
たし算の筆算をするとき、まずは一の位を計算しましょう。7と5をたすと12になります。12の一の位は2です。そこで、2を一の位にかきましょう。
また、12の十の位は1です。そこで、十の位に1をくわえましょう。以下のようになります。
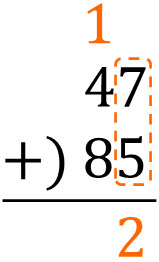
そのあと、十の位をすべてたします。以下のようになります。
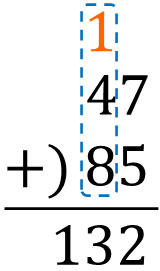
こうして、答えが132とわかりました。筆算をするときのやり方をおさらいすると以下のようになります。
- 一の位の7と5をたして12
- 12のうち、一の位の2をかく
- 12のうち、十の位の1をくわえる
- 十の位を計算する
さきに一の位を計算したあと、つぎに十の位を計算しましょう。
・3ケタのたし算をする
それでは、2ケタではなく3ケタのたし算ではどうでしょうか。このときについても、さきほどとやり方はおなじです。たとえば、以下の計算はどのようにすればいいのでしょうか。
- \(285+439\)
2ケタの計算では、さきに一の位を計算しました。そのあと、十の位を計算します。3ケタの計算もおなじであり、一の位、十の位、百の位を順番に計算します。
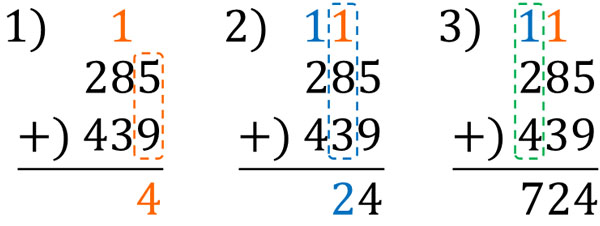
2ケタの筆算をすることができれば、3ケタのたし算は難しくありません。やり方を覚えて、計算できるようにしましょう。
2ケタや3ケタの引き算の筆算をする
たし算を学んだあと、つぎに勉強するべきはくり下がりのある引き算です。2ケタや3ケタの引き算はどのように筆算すればいいのでしょうか。さきほどと同じように、筆算によって問題をときましょう。
たとえば、以下の計算をします。
- \(53-27\)
つくる式は以下になります。
\(\begin{array}{rr}
& 53\\
-\big{)}&27\\
\hline
\end{array}\)
たし算とおなじように、一の位を計算したあと、十の位を計算しましょう。以下のようになります。
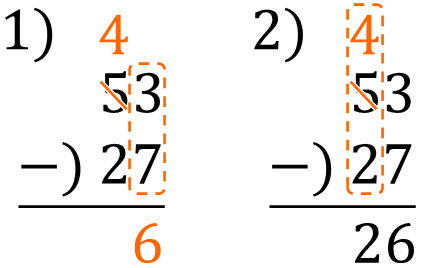
\(3-7\)をすることはできません。そこで、53から10を借りましょう。10を借りるため、\(13-7=6\)になります。
次の計算は十の位です。ただ、53は10を貸しています。そのため、十の位は5ではなく4になっています。十の位の4から2を引くことで、答えをだすことができます。
この計算では、53を以下のように分けています。
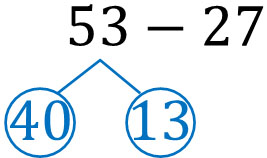
\(3-7\)ができないため、\(13-7\)にしました。また53を40と13にわけることによって、十の位は5ではなく4になっています。さきほどの筆算では、十の位を5から4にしました。この理由としては、53をわけるときに40がつくられるからです。
・3ケタの引き算をする
2ケタの引き算ができるようになれば、3ケタの引き算をすることができます。たとえば、以下はどのように筆算すればいいでしょうか。
- \(616-268\)
まずは筆算の式をつくりましょう。以下のようになります。
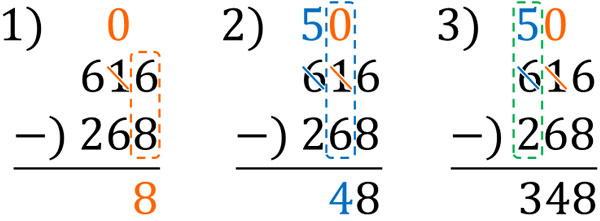
引き算をすることができない場合、一つ大きいケタから数字を借りましょう。数字を借りることによって、引き算ができるようになります。
くり上がり、くり下がりのある計算をする
小学算数でさいしょに習う内容がたし算と引き算です。ただたし算をするとき、くり上がりがあることは多いです。また、くり下がりのある引き算の計算をしなければいけないこともあります。
そこで、どのように計算すればいいのか理解しましょう。2ケタと1ケタの計算をするとき、キリのよい数をみつけるといいです。10や20、30などがキリのよい数です。キリのよい数を使うことによって、くり上がりやくり下がりの計算ができます。
また筆算では、2ケタや3ケタの整数を計算することがあります。ケタの大きい整数についても、計算できるようにしましょう。
たし算と引き算にはやり方があります。くり上がりやくり下がりのある計算について、どのように問題を解けばいいのか理解しましょう。