小学校の算数では偶数と奇数を勉強します。それでは、偶数や奇数とは何なのでしょうか。また、どのように偶数と奇数を見分ければいいのでしょうか。
日常生活で偶数と奇数の概念は頻繁に利用されます。たとえば、プログラミングでは偶数と奇数を利用します。また買い物で偶数と奇数を利用することがあります。
偶数と奇数には性質があります。そこで偶数と奇数を見分けられるようになるだけでなく、たし算や引き算、かけ算をした後の答えがどのような数字になるのか分かるようにしましょう。そこで、偶数と奇数の見分け方や計算方法を解説していきます。
もくじ
偶数・奇数とは何か:定義と言葉の意味
まず、小学算数で学ぶ偶数と奇数とは何でしょうか。言葉の定義を理解することで、どのような数字なのか理解できるようになります。
偶数と奇数は以下のように定義されます。
- 偶数:2でわれる数
- 奇数:2でわれない数
ある数を2でわれる場合、その数を偶数といいます。また2でわり切れない数を奇数といいます。たとえば32は偶数でしょうか、それとも奇数でしょうか。以下のように、32は2でわることができます。
- \(32÷2=16\)
そのため、32は偶数です。
また2でわれる数が偶数であるため、2に対して2ずつ増える場合、必ず偶数になります。別の言葉でいうと、2の倍数は偶数になります。
- 2、4、6、8、10、12、14…
これらの数はすべて偶数です。
一方、17は偶数でしょうか、それとも奇数でしょうか。17は2でわり切ることができません。答えに余りの数が出てしまいます。
- \(17÷2=8\) あまり 1
そのため、17は奇数です。2でわれるかどうかによって、偶数と奇数を見分けることができます。別の言葉でいうと、1に対して2ずつ増える場合はすべて奇数になります。
- 1、3、5、7、9、11、13…
これらの数はすべて奇数です。偶数も奇数も、2ずつ数が増えていきます。
偶数と奇数の見分け方・覚え方
それでは、どのようにして偶数と奇数を効率的に見分ければいいのでしょうか。前述の通り、2でわれる場合は偶数です。それ以外の数は奇数です。別の言葉でいうと、2の倍数は偶数です。一方、2の倍数でない場合は奇数です。
そこで、1の位に着目しましょう。以下のように偶数と奇数を見分けることができます。
- 偶数:1の位が0、2、4、6、8
- 奇数:1の位が1、3、5、7、9
どんなに大きな数でも、1の位が「0、2、4、6、8」の場合、その数は偶数です。またどんなに大きな数でも、1の位が「1、3、5、7、9」の場合、その数は奇数です。1の位を確認すれば、偶数か奇数かを判別できます。10の位や100の位の数が偶数か奇数かどうかは関係ありません。
たとえば、395374は偶数でしょうか。それとも奇数でしょうか。395374を確認すると、1の位は4です。4は偶数なので、395374は偶数です。事実、395374は2でわることができます。
- \(395374÷2=197687\)
偶数か奇数かを確認するには、1の位をチェックしましょう。
たし算・引き算による答えは偶数か奇数か?
それでは、次にたし算または引き算をすることによって答えが偶数と奇数のどちらになるのかを考えてみましょう。たし算をするとき、以下のような性質があります。
- 奇数+奇数=偶数
- 奇数+偶数=奇数
- 偶数+奇数=奇数
- 偶数+偶数=偶数
理由を説明するとなると、中学数学を利用した証明をしなければいけません。そのため理由は省きますが、必ず上記のようになります。そこで、以下のように簡単な整数で考えてみましょう。

このように、偶数または奇数のたし算によって答えがどのようになるのか理解しましょう。
一方、引き算ではどのようになるのでしょうか。たし算と同様、引き算でも以下のように同じ結果になります。
- 奇数-奇数=偶数
- 奇数-偶数=奇数
- 偶数-奇数=奇数
- 偶数-偶数=偶数
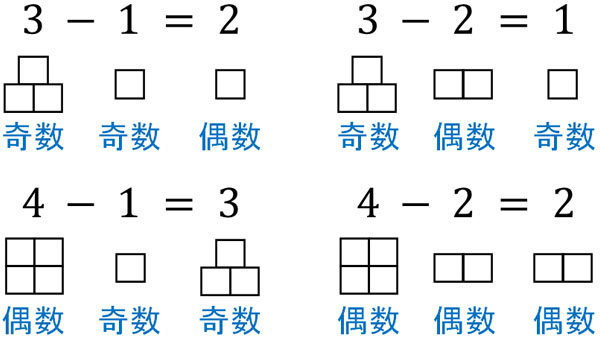
偶数と奇数を考える場合、同じ性質の数(奇数と奇数、または偶数と偶数)のたし算や引き算では、答えが偶数になります。一方、違う性質の数(偶数と奇数)のたし算や引き算では、答えが奇数になります。なお、この性質は大きい数字であっても成り立ちます。
かけ算で答えは偶数なのか、奇数なのか
それでは、かけ算ではどのようになるのでしょうか。かけ算の場合、偶数が含まれる数字をかけると、必ず答えが偶数になります。小学校の算数で倍数を習っている場合、この理由を理解できます。
前述の通り、2でわれる数が偶数です。偶数とは、2の倍数でもあります。また2を掛ける場合、当然ながら必ず答えは2の倍数になります。
- \(1×\color{red}{2}=2\):偶数
- \(2×\color{red}{2}=4\):偶数
- \(3×\color{red}{2}=6\):偶数
- \(4×\color{red}{2}=8\):偶数
また2だけでなく、偶数をかける場合、必ず答えは偶数になります。偶数は2の倍数だからです。
- \(3×\color{red}{4}=12\):偶数
- \(3×\color{red}{6}=24\):偶数
- \(5×\color{red}{8}=40\):偶数
- \(6×\color{red}{10}=60\):偶数
かけ算で答えが奇数になるのは、奇数同士を掛けるときのみです。以下のように、奇数と奇数のかけ算では答えが奇数になります。
- \(1×3=3\):奇数
- \(5×7=35\):奇数
- \(3×9=27\):奇数
- \(7×11=77\):奇数
つまりかけ算では以下のようになります。
- 奇数×奇数=奇数
- 奇数×偶数=偶数
- 偶数×奇数=偶数
- 偶数×偶数=偶数
たし算や引き算とは異なり、かけ算では答えが偶数になる確率が高いです。答えが奇数になるには、奇数同士を掛ける必要があります。
偶数と奇数の性質を理解する
頻繁に利用される概念として偶数と奇数があります。日常生活で偶数と奇数を使う場面は多いため、どのように偶数と奇数を見分ければいいのか理解しましょう。
2でわれる場合、その数字は偶数です。また2でわって余りの数が出る場合、その数字は奇数です。偶数か奇数かを見分ける方法として、1の位に着目しましょう。1の位を確認すれば、偶数なのか奇数なのか見分けられるようになります。
また、たし算や引き算をするとき、答えがどのようになるのか理解しましょう。偶数同士または奇数同士のたし算や引き算では、答えは偶数になります。一方で偶数と奇数を利用してたし算または引き算をする場合、答えは奇数になります。
これらの性質を理解しましょう。偶数や奇数を理解していない場合、日常生活で困ることになります。大人では何度も偶数や奇数を利用するため、これらの定義や概念を学びましょう。