小数しょうすうの計算を小学算数で学びます。1よりも小さい数を含めてあつかうのが小数です。わたしたちの日常生活にちじょうせいかつでも、小数を使うことはひんぱんにあります。

そこで、小数とはなにかをまずは理解りかいしましょう。小数の仕組みを学ぶことによって、どのようなときに小数を利用するのかわかります。

また小数のたし算と引き算をできるようにしましょう。たし算や引き算ではケタを合わせる必要ひつようがあり、やり方を理解しなければいけません。そこで、どのように小数の計算をすればいいのか解説かいせつしていきます。

小数とはなにか？なぜ必要なのか

まず、小数とはなんでしょうか。たとえば、以下のような数を小数といいます。

  • 0.4
  • 0.241
  • 12.24

0.1や0.2は1よりも小さい数を表します。つまり、1より小さい数が含まれているのが小数といえます。0と1の間あいだに数があり、1を10等分したものが0.1です。「1を\(\displaystyle\frac{1}{10}\)にすると0.1になる」ともいえます。

また、1を100等分すると0.01になります。「1を\(\displaystyle\frac{1}{100}\)にすると0.01になる」ともいえます。つまり、0.1よりも小さい数があります。

ほかには、1を1000等分すると0.001になります。このように小数を使うことによって、小さい数をあらわせるようになります。

それでは、なぜ小数を学ぶ必要があるのでしょうか。それは、日常生活で小数がたくさん使われるからです。たとえば、以下のケーキはあわせていくつでしょうか。

ここには、3つのケーキと0.2つのケーキがあります。そのため、「3.2個このケーキがある」と表現ひょうげんします。

1よりも小さい数字を使わなければいけない場面ばめんはたくさんあります。算数で小数が重要じゅうようなのは、利用することが多いからです。

小数の位の呼びかた

つぎに、小数の位の呼びかたについて学びましょう。小数はそれぞれ以下のようにいいます。

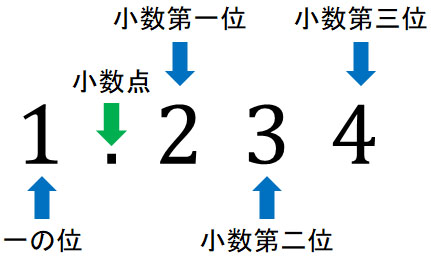
また小数は以下のように、\(\displaystyle\frac{1}{10}\)の位、\(\displaystyle\frac{1}{100}\)の位のように表されることもあります。

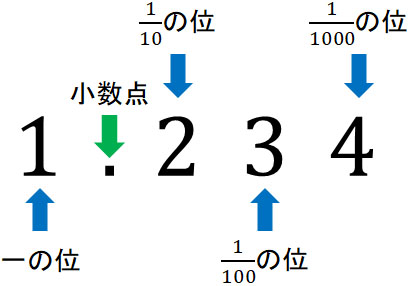
どちらであっても、意味を理解できるようにしましょう。

小数の仕組みと関係

それでは、小数はどのような仕組しくみになっているのでしょうか。また、数字はそれぞれどのような関係かんけいになっているのでしょうか。

すでに解説かいせつした通り、1の\(\displaystyle\frac{1}{10}\)が0.1です。また、1の\(\displaystyle\frac{1}{100}\)が0.01です。さらには、「0.1の\(\displaystyle\frac{1}{10}\)が0.01になる」と考えることもできます。以下のような関係になっています。

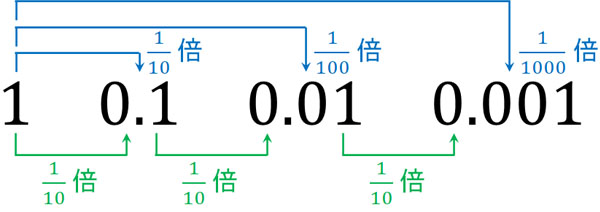
また、0.1を10倍すると1になります。0.01の100倍は1です。そのため、0.01を10倍すると0.1になります。以下のような関係になります。

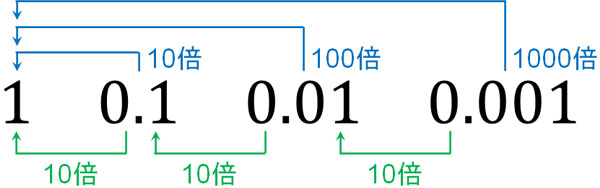
このような関係になっているため、それぞれの位を区別くべつしましょう。

たとえば、1.3はどのような数字でしょうか。1.3とは、「1を1つ、0.1を3つ合わせた数」といえます。以下のようになります。

また1.3とは、0.1を13つ合わせた数ということもできます。以下のように、0.1が13あることによって1.3になります。

0.1を10倍すれば1になります。そのため、0.1が13つあると1.3になるのです。このように、小数がどのような仕組みになっているのか確認しましょう。

小数のたし算の計算方法

ここまでの内容ないようを理解したうえで、小数のたし算をしましょう。小数のたし算をするとき、これまで習ったたし算の方法ほうほうとやり方は同じです。たとえば、以下のようになります。

  • \(0.1+0.3=0.4\)
  • \(0.2+0.5=0.7\)

小数点はあるものの、数字のたし算をすることによって小数のたし算をすることができます。

このとき重要なのは、かならずケタをそろえなければいけないことです。これは、ケタを合わせなければ正しく計算できないからです。たとえば\(21+243\)をするとき、筆算ひっさんで左にそろえるのは間違まちがいであるといえます。

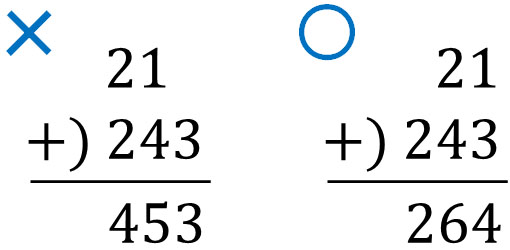
そこで、ケタを合わせましょう。小数のたし算であれば、小数点の位置を合わせるのです。たとえば、以下の計算はどのようにすればいいでしょうか。

  • \(12.4+4.174\)

この計算をするとき、ケタを合わせましょう。そこで、以下のような筆算の式を作ります。

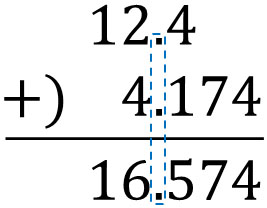
小数点を合わせれば、あとはたし算をするだけです。同じケタどうしでたし算をしましょう。

なお注意点として、小数点の計算では、場合によってはゼロを消さなければいけないことがあります。一番小さいケタが0のとき、小数のたし算をしたあとに0を消しましょう。たとえば、以下のようになります。

  • \(3.47+1.13=4.6\)
  • \(12.75+2.25=15\)

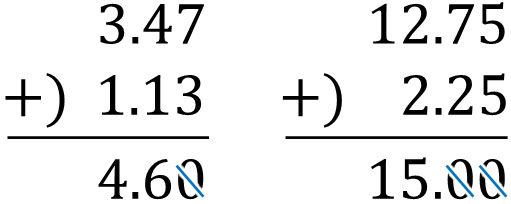
参考さんこうまでに、一番小さいケタが0のとき、0を消さなければいけないのは引き算でも同じです。小数では、下のケタに0が隠かくされています。ただ小さいケタの数がゼロのとき、0を省略しょうりゃくするというルールがあります。

小数の引き算をするときの計算方法

一方で引き算はどのようにすればいいのでしょうか。小数の引き算について、これまで習ってきた引き算とやり方は同じです。たし算と同じように、ケタ数を合わせて引き算をしましょう。

重要なポイントは小数点を合わせることです。たとえば、以下の計算をしてみましょう。

  • \(5.4-2.8\)

筆算をすると、次の式になります。

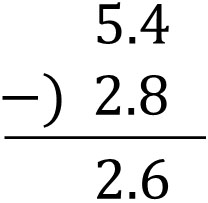
引き算をするときに、とくに難むずかしいことはありません。小数点はあるものの、これまで習った引き算のやり方と同じです。

なお一の位が0になるとき、必ず0を書くようにしましょう。以下のようになります。

  • \(1.5-0.9=0.6\)

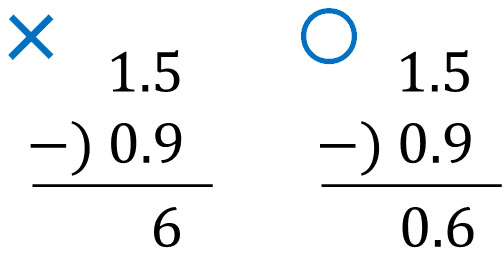
前に解説したとおり、ケタを必ず合わせなければいけません。そのため小数の計算するとき、一の位が0であったとしても、小数点と0は必ず書くようにしましょう。

ケタが多いときの小数の引き算

またほかにも、ケタが多い引き算のやり方を学びましょう。たとえば、以下の計算はどのようにすればいいでしょうか。

  • \(19.3-2.147\)

小数点を合わせなければいけないのは共通きょうつうです。それにくわえて、0をつけましょう。19.3ではなく、19.300にするのです。以下のようになります。

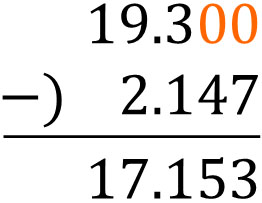
前に説明したとおり、小数点の右には0が隠れています。無限むげんに0が続つづいていくため、通常つうじょうは0を省略しょうりゃくします。ただケタの異ことなる数の引き算をするときについては、必要であれば0をくわえましょう。

小数の概念を学び、たし算と引き算をする

わたしたちにとって、小数の概念がいねんを学ぶことは重要です。買いものなど、日常生活でひんぱんに小数を使うからです。1よりも小さい数を利用しなければいけない場面はたくさんあります。

このとき、数字の計算ができなければいけません。たし算や引き算をすることによって、必要な数字を計算できるようになります。そこで小数点の位置やケタ数を必ずあわせ、計算するようにしましょう。そうしなければ、計算ミスをしてしまいます。

小数を使う場面は多いです。そこで小数の考え方を理解して、計算できるようになりましょう。